합병 정렬(merge sort)알고리즘이란, 분할 정복(divide and conquer) 기반인 정렬 알고리즘이다.
쉽게 말하자면, 더 이상 쪼개질 수 없을 정도의 단위로 쪼갠 후에, 합병하면서 정렬하는 것이다.
일단 합병 정렬 알고리즘의 실행시간은 재귀적 표현을 가지고 있기 때문에, 값을 직접적으로 알 수 없다는 특징이 있다.
e.g. T(n) = T(n-1) + 2

자, 먼저 배열을 최소 단위로 먼저 쪼개는 방법이다.
배열 A가 p부터 r까지의 원소를 가진다면, 그 중간값인 q를 먼저 찾는다.
⌊⌋이런 기호가 보이는데, floor연산이며 안의 값보다 크지 않는 최대의 정수(내림)값을 찾는 연산이다.
그리고 나눠진 배열에서의 각각 중간값을 찾는 과정을 반복한다(재귀).

$n_1$에는 배열A의 처음 원소부터 중간값까지의 원소 개수가 들어가고, $n_2$에는 나머지 원소의 개수가 들어간다.
그리고 배열 L[1...$n_1$+1]과 배열 R[1...$n_2$+1]을 만들어준다.
i가 1부터 $n_1$까지일 때, A[p + i -1]의 값을 L[i]에 대입하는 것을 반복하고,
j가 1부터 $n_2$까지일 때, A[q + j]의 값을 R[i]에 대입하는 것을 반복한다.
이 과정을 거치면, 배열 A가 배열 L과 배열 R로 나눠진다.
배열 L과 배열 R에 칸을 한칸 더 만들어준 뒤, 무한대를 넣어준다.
i와 j에 1을 대입한다.
k가 p부터 r까지 일때,
배열 L[i]와 R[j]를 비교하고, 더 작은 수를 배열 A의 왼쪽에 대입한다.
배열 L[i]가 더 작은 수를 가졌다면, i의 값을 1 올려준다.
그러고난 뒤에는 L[i+1]과 R[j]의 값을 비교하여, 작은 수를 배열 A에 대입한다.
이 과정을 반복하면 정렬된 배열이 완성된다.
무한대를 끝에 삽입해 놓은 이유는, 배열 L나 배열 R중 하나의 배열의 정렬이 다 끝났을 때를 대비하기 위해서다.
만약 배열 L의 정렬이 먼저 다 끝나고 i를 오른쪽으로 한칸 옮기면 L[i]는 무한대의 값을 갖게 될 것이고, 자연스레 R[j]는 더 작은 값이 되어 정렬이 될 것이다.

합병 정렬 알고리즘의 실행시간을 분석해본다.
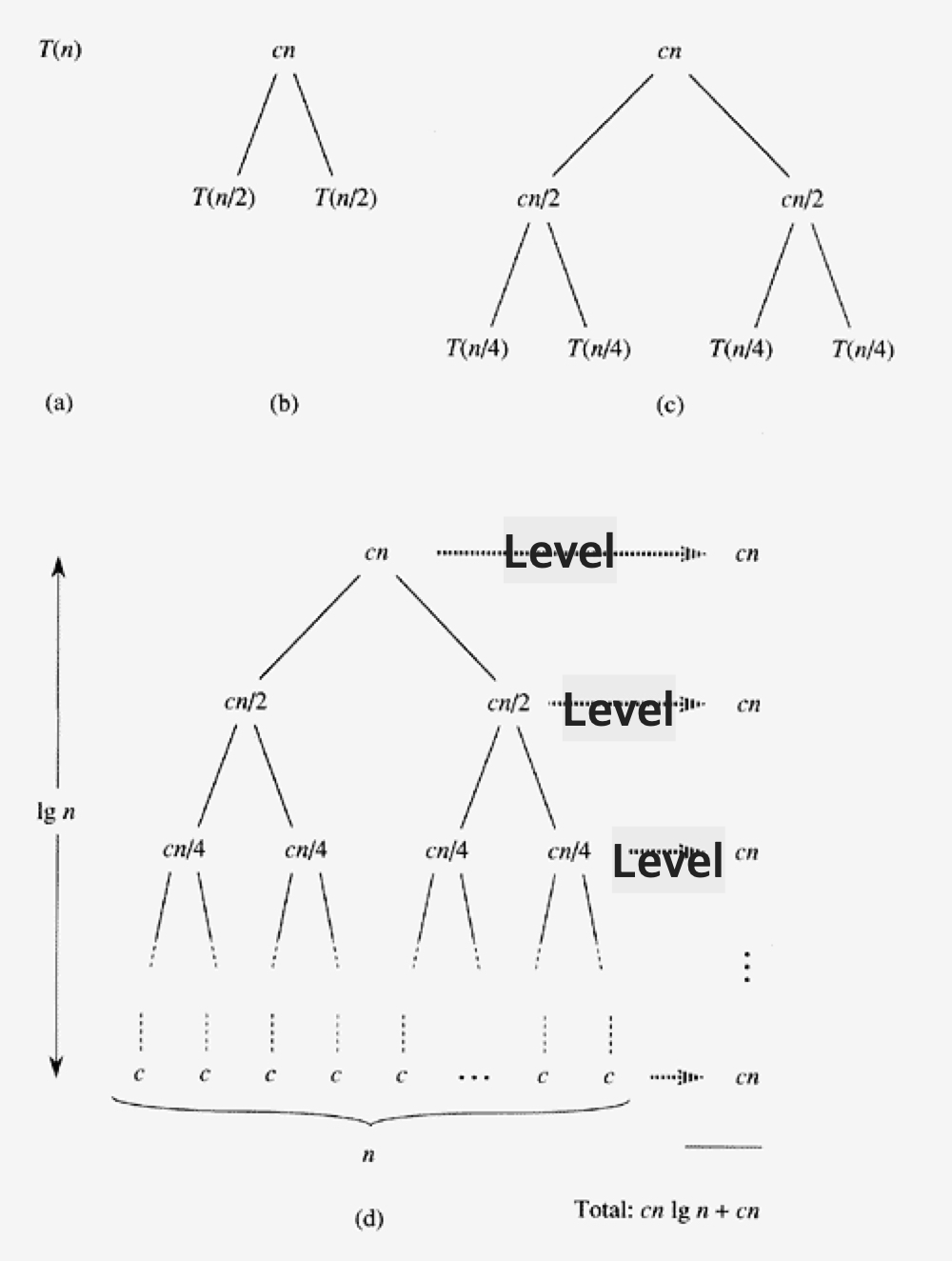
c(n)은 병합되는 시간을 뜻한다.
T(n)은 먼저 그림(b)처럼 두 개의 배열로 나뉜다. → T(n) = T(n/2) + T(n/2) + c(n)
T(n/2)도 그림(c)처럼 각각 두개의 배열로 나뉜다. → T(n/2) = T(n/4) + T(n/4) + c(n/2)
・・・
여기서 T(n)은 재귀함수이기 때문에 정확한 값을 구하지 못하고, 사실상 병합되는 시간이 실질적 실행 시간으로 남게 된다.
때문에 그림(d)처럼 각 레벨 당 c(n)의 값만이 남게된다.
트리 구조에서 높이(h)를 구하면 $\lg{n}$가 되는데, 따라서 $cn × \lg{n} + cn$이 실행시간이 된다.
→ 빅오 표현법으로 $O(n\lg{n})$의 시간이 걸린다.
** 대학교 수업을 듣고 이해한 부분을 최대한 풀어서 작성한 글입니다.
틀린 정보가 존재할 수 있으며, 언제나 피드백은 환영입니다. **
'DKU > 알고리즘 및 실습' 카테고리의 다른 글
| Bubble Sort Algorithm (0) | 2024.10.03 |
|---|---|
| Growth of Functions (0) | 2024.09.26 |
| Insertion Sort Algorithm (0) | 2024.09.11 |
| Getting Started (4) | 2024.09.10 |
| The Role of Algorithms in Computing (0) | 2024.09.04 |
