그래프 알고리즘을 배우기에 앞서, 그래프란 무엇일까?
그래프는 $G = (V, E)$는 정점 집합 V와 간선 집합 E로 이루어져 있으며, 방향성이 있을 수도 있고 없을 수도 있다.
알고리즘에서 사용하는 그래프 표현 방법에는 두가지가 존재한다.
- 인접 리스트(Adjacency list): 각 정점에 연결된 이웃 정점들을 리스트 형태로 저장한다.
- 인접 행렬(Adgacency matrix): 정점 간의 연결을 행렬 형태로 표현하여, 특정 정점 쌍 간의 연결 여부를 나타낸다.
알고리즘의 실행 시간은 보통 정점의 수 |V|와 간선의 수 |E|로 표현된다.
점근 표기법을 사용할 때는, 집합의 크기를 나타내는 기호는 생략할 수 있다. $O(V + E)$로 간단히 표현할 수 있다는 의미이다.
인접 리스트: Adjacency list
인접 리스트는 |V|개의 리스트로 이루어진 배열이다. 각 정점에 대해 하나의 리스트가 있으며, 그 리스트에는 해당 정점과 연결된 모든 인접 정점이 포함된다.
정점 u의 리스트에는 $(u, v) \in E$인 모든 정점 v가 포함된다. 이 방식은 방향 그래프와 무방향 그래프에서 모두 사용할 수 있다.

그림 (a)는 5개의 정점과 7개의 간선이 있는 무방향 그래프이고, 그림 (b)는 (a)의 인접 리스트이다. 그림 (c)는 그림 (a)의 인접 행렬이다.
인접 리스트를 사용하는 그래프의 공간 복잡도는 $\Theta(V + E)$이다.
정점 $u$에 인접한 모든 정점을 나열하는데 걸리는 시간은 $\Theta$(degree(u))이며, 간선의 존재 여부를 확인하는데 걸리는 시간은 $O$(degree(u))이다.

방향 그래프도 위의 그림처럼 표현되는데, 공간 복잡도와 시간 복잡도는 무방향 그래프와 동일하다.
인접 행렬: Adjacency Matrix
인접 행렬은 |V| × |V| 크기의 행렬 A = ($a_{ij}$)로 표현된다.
인접 행렬을 사용하는 그래프의 공간 복잡도는 $\Theta(V^2)$이다.
정점 u에 인접한 모든 정점을 나열하는데 걸리는 시간은 $\Theta(V)$ 이며, 간선의 존재 여부를 확인하는데 걸리는 시간은 $O(1)$이다. 즉, 행렬의 해당 요소를 즉시 참조할 수 있다.
Breadth-First Search: 너비 우선 탐색, BFS
일단은 간선 가중치가 없는 경우를 탐색해보자. 여기서는 d[v]만 계산하고, $\pi$[v]는 생략한다. 또한 정점의 색깔 정보도 생략한다.
- Input: 그래프 $G = (V, E)$로, 방향 그래프일 수도 있고 무방향 그래프일 수 있다. 또한 시작 정점(source vertex) $s$ 가 주어진다.
- Output: 각 정점 $v$에 대해 d[v]가 출력된다. 이는 s에서 v까지의 거리(가장 적은 간선의 수)이다. 여기서 $\pi$[v]는 v의 직전 정점(predecessor) u로, (u, v)가 최단 경로 상의 마지막 간선이 된다.
BFS는 시작 정점 s에서 파도를 퍼뜨리듯 탐색을 진행한다.
먼저 s에서 한 간선 거리에 있는 모든 정점에 도달하고, 그 다음 s에서 두 간선 거리에 있는 모든 정점에 도달하는 식으로 탐색이 확장된다.
여기서 탐색의 파도 전선(wavefornt)을 관리하기 위해 FIFO 큐 Q를 사용한다. 정점 v가 큐 Q에 들어 있다는 것은 파도가 v에 도달했지만, 아직 v를 통해 확장되지 않았다는 의미이다.

코드를 보면 WHITE, GRAY, BLACK의 색깔을 볼 수 있다. WHITE는 아직 방문되지 않은 정점을, GRAY는 현재 방문 중인 정점을, BLACK은 방문이 끝난 정점을 의미한다.
먼저 그래프에서 시작 정점을 뺀 모든 정점에 WHITE를 넣어준다. d[u]에는 무한대 값을, $\pi$[u]에는 NIL값을 넣어 초기화해준다.
그 후에 시작 정점에 GRAY색을 넣어주고, d[s]에는 0, $\pi$[s]에는 NIL값을 넣으며 탐색의 시작을 준비한다. 시작 정점의 거리는 0이고, 직전 정점은 존재하지 않으니 이러한 값을 대입해주는 것이다.
탐색이 이루어지는 과정은 다음 방향성이 없는 그래프의 그림을 보면서 알아보도록 하자.

(a) - 위에서 설명한 것처럼 탐색을 시작할 준비를 마친 상태이다. 이때, Q에 s를 입력한다(ENQUEUE).
(b) - Q에 s 데이터가 입력됐으니, 탐색을 진행할 수 있게 되었다. Q에서 s라는 데이터를 출력하여(DEQUEUE) u에 넣어준다. Adj[u]는 인접한 정점들을 뜻하며, 여기서는 r과 w를 뜻한다. 인접한 정점의 색이 WHITE면 GRAY로 바꿔주고, d[r]과 d[w]에 d[u]+1인 1 값을 대입한다. $\pi$[r, w]는 u가 된다. 이제 큐에 r과 w를 넣어주고, 탐색을 마친 s의 색은 BLACK으로 바꿔준다.
(c) - r보다 먼저 w를 보도록하자. w가 DEQUEUE 되어 u에 들어가게 되었고, 인접한 정점인 t와 x가 ENQUEUE 되었다.
(d) - r 정점을 처리하여 Q에 v가 들어오게되었다.
(e) - t 정점을 처리했다.
(f) - x 정점을 처리했다.
(g) - v 정점을 처리했으며, 이때 v정점에 인접한 노드가 없기 때문에 Q에는 추가되는 값이 없다.
(h) - u 정점을 처리했으며, 이때 u정점에 인접한 노드가 없기 때문에 Q에는 추가되는 값이 없다. (y 정점은 이미 Q에 있을 뿐더러 최단 거리가 아님)
(i) - y 정점을 처리했으며, 이제 Q에는 데이터가 남지 않았다.
이제 BFS 알고리즘으로 탐색이 된 그래프는, d[v]의 값을 통해 트리를 그릴 수 있게 되었다.
Q는 거리 값 d를 가진 정점들로 구성된다. 위의 그림을 보면 알 수 있다싶이, Q에는 한번에 1개 또는 2개의 d값만이 존재한다. 만약 서로 다른 두 개의 d값이 존재한다면, 값 차이는 1이 되고 작은 값들이 먼저 나타난다.
여기서 각 정점은 딱 한번, 유한한 d값을 부여받으며, 정점에 할당되는 d값은 시간이 지남에 따라 단조 증가(monotonically increase)한다.
하지만 BFS는 모든 정점에 도달하지 못할수도 있다는 문제를 가지고 있다. 예를 들어, 그래프가 연결되지 않은 경우, 시작 정점과 연결되지 않은 정점들은 탐색되지 않는다.
시간 복잡도는 $O(V + E)$가 된다.
여기서 $O(V)$는 각 정점이 최대 한번 Q에 추가되는 시간이며, $O(E)$는 각 정점이 최대 한번 Q에서 제거될 때, 간선(u, v)가 탐색되는 시간이다. 따라서, 각 간선은 무방향 그래프에서는 최대 두번 탐색되고 방향 그래프에서는 최대 한번 탐색된다.

s부터 v까지의 경로를 출력하는 알고리즘이다.
시작 정점 s를 출력하고, $\pi$[v]를 사용하여 직전 정점을 찾아가 경로를 출력하는 것이다.
물론, 알고리즘은 재귀적으로 호출된다.
Depth-First Search: 깊이 우선 탐색, DFS
BFS와 다른 점을 먼저 말하자면, DFS는 큐 없이 재귀적으로 동작한다.
- Input: 그래프 $G = (V+E)$만이 입력 데이터다. 시작 정점 s는 존재하지 않는다.
- Output: 각 정점에 대해 두 개의 타임스탬프를 기록한다. d[v]는 정점 v가 처음 발견된 시간이며, f[v]는 정점 v가 탐색을 마친 시간이다. $\pi$[v]는 BFS와 마찬가지로 직전 정점을 의미한다.
DFS는 모든 간선을 체계적으로 탐색한다. 필요에 따라서는 다른 정점에서 탐색을 다시 시작하는 것도 가능하다.
BFS와는 다르게 정점을 발견하면 큐에 넣어 나중에 탐색하지 않고, 즉시 탐색을 시작한다.
각 정점의 발견 시간과 종료 시간은 1부터 2|V| 사이의 고유한 정수로 지정되며, 모든 정점에 대해 d[v] < f[v]가 성립된다.

주어진 입력 그래프의 모든 정점을 u라고 한다.
u에 WHITE라는 색상을 넣어주고, $\pi$[u]에는 NIL값을, 타임스탬프 time에는 0값을 넣어주며 초기화해준다.
후에 임의의 정점 u를 선택하고, 그 정점의 색상이 WHITE라면 DFS-Visit(u) 함수를 호출한다.
DFS-Visit(u)가 호출되면, u 정점의 색상을 일단 GRAY로 바꿔준다.
타임스탬프의 값은 1 증가시켜주며, d[u]에 증가된 타임스탬프 값을 넣어준다. 이는 정점 u에 도착한 시간을 의미한다.
정점 u에 인접한 각 노드 v에 대하여, v 정점의 색상이 WHITE라면 $\pi$[v]에 u를 대입해주고, 다시 DFS-Visit(v)함수를 호출한다. 재귀적으로 작동하며 후속 정점들의 탐색을 계속하는 것이다.
재귀가 끝나면, 정점 u의 색상은 BLACK으로 바꿔준다. 또한 타임스탬프 값을 증가시켜, f[u]에 대입한다. 정점 u의 탐색을 끝낸 시간을 의미한다.
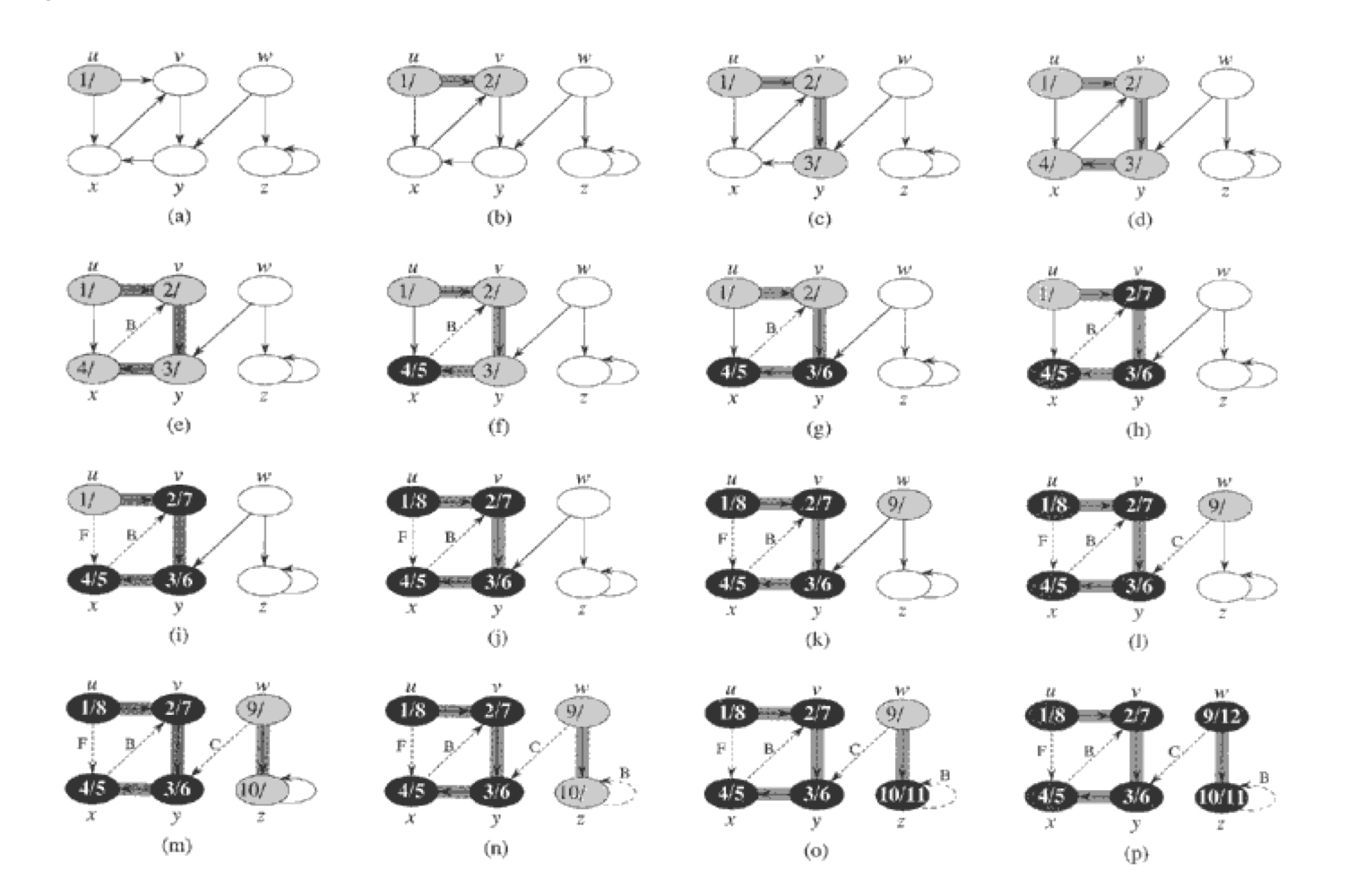
그림을 보면서 이해해보도록 하자.
(a) - 초기화를 완료하고, d[u] = 1의 값을 기록하고 탐색을 시작한다.
(b) - 우측으로 먼저 향했다고 가정한다. 정점 v를 탐색하고, d[v] = 2의 값을 기록한다.
(c) - 정점 y를 탐색하고, d[y] = 3의 값을 기록한다.
(d) - 정점 x를 탐색하고, d[x] = 4의 값을 기록한다.
(e) - 정점 x의 방향을 따라 갔더니, 이미 탐색된 정점 v이다. 이때의 간선을 B(Backward) 간선이라고 하며, x의 조상을 조사했다는 의미이다.
(f) - 재귀를 끝낸 정점 x에 f[x] = 5의 값을 기록한다.
(y) - 탐색했던 방향을 다시 거꾸로 되돌아가며 정점 y에 f[y] = 6의 값을 기록한다.
(h) - 정점 v에 f[v] = 7의 값을 기록한다.
(i) - 정점 u의 남아있는 간선을 조사한다. 이를 F(Forward)간선이라고 하며, u의 후손을 조사했다는 의미이다.
(j) - 정점 u에 f[u] = 8의 값을 기록한다.
(k) - 임의의 정점 w가 선택되었으며, d[w] = 9의 값을 기록하고 탐색을 시작한다.
(y) - w의 간선을 탐색했더니, 조상도 아닌 후손도 아닌 이미 탐색이 끝난 다른 정점과 이어져있다. 이를 C(cross)간선이라고 한다.
(m) - w의 또다른 간선을 탐색했다. 정점 z를 탐색하고, d[z] = 10의 값을 기록한다.
(n) - 정점 z의 간선을 따라가니 z 본인이 되며, 재귀를 종료한다. 이 역시 B간선이라고 하며 f[z] = 11의 값을 기록한다.
(p) - 정점 w에 f[w] = 12의 값을 기록한다.
그래프의 탐색이 완료되고, 총 2개의 트리가 생성된다.
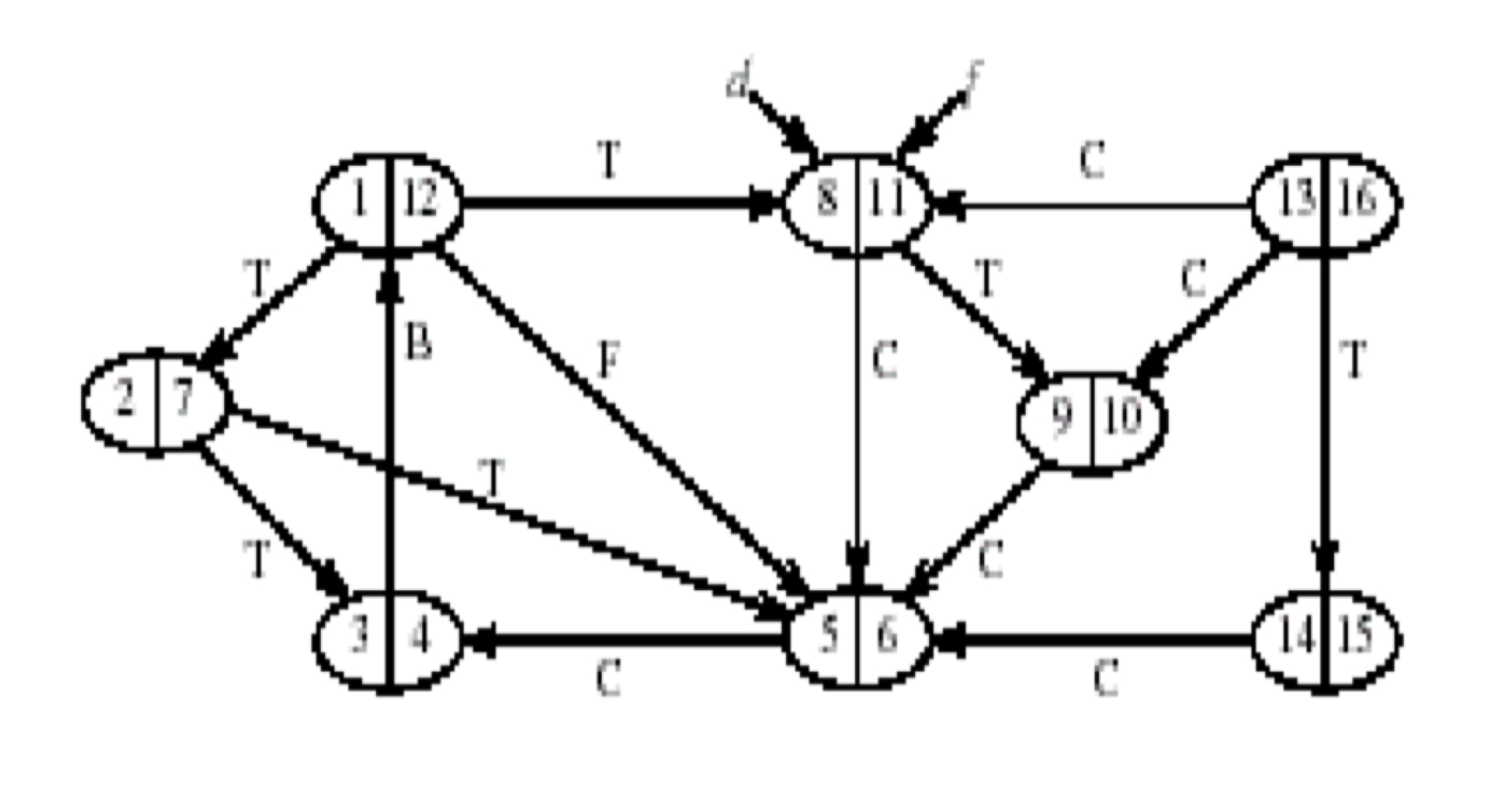
위 사진은 DFS의 다른 예시이다. B, F, C의 세가지 간선을 볼 수 있다.
T 간선은 Traverse라는 의미로, 이동 중(탐색 중)인 간선을 의미한다.
DFS의 시간 복잡도는 $\Theta(V + E)$이다.
DFS는 모든 정점과 간선을 반드시 탐색하므로 $\Theta$ 표기법을 사용하는 것이다.
DFS는 깊이 우선 포레스트(depth-first forest)를 형성하며, 여러 개의 깊이 우선 트리(depth-first tree)로 구성된다.
위의 설명에서 트리가 2개 생기지 않았는가?
여기서 각 트리는 간선(u, v)로 이루어져 있으며, 이때 u는 GRAY 상태이고 v는 WHITE 상태일 때 해당 간선을 탐색한다.
DFS의 이론에는 괄호 정리(Parenthesis theorem)가 있다.
모든 정점 u와 v에 대해, 정확히 다음 중 하나가 성립하는 것이다.
- d[u] < f[u] < d[v] < f[v] 또는 d[v] < f[v] < d[u] < f[u]: 이 경우 u와 v는 서로의 자손이 아니다.
- d[u] < d[v] < f[v] < f[u]: 이 경우 v는 u의 자손이다.
- d[v] < d[u] < f[u] < f[v]: 이 경우 u는 v의 자손이다.
따라서, d[u] < d[v] < f[u] < f[v]는 성립할 수 없다.
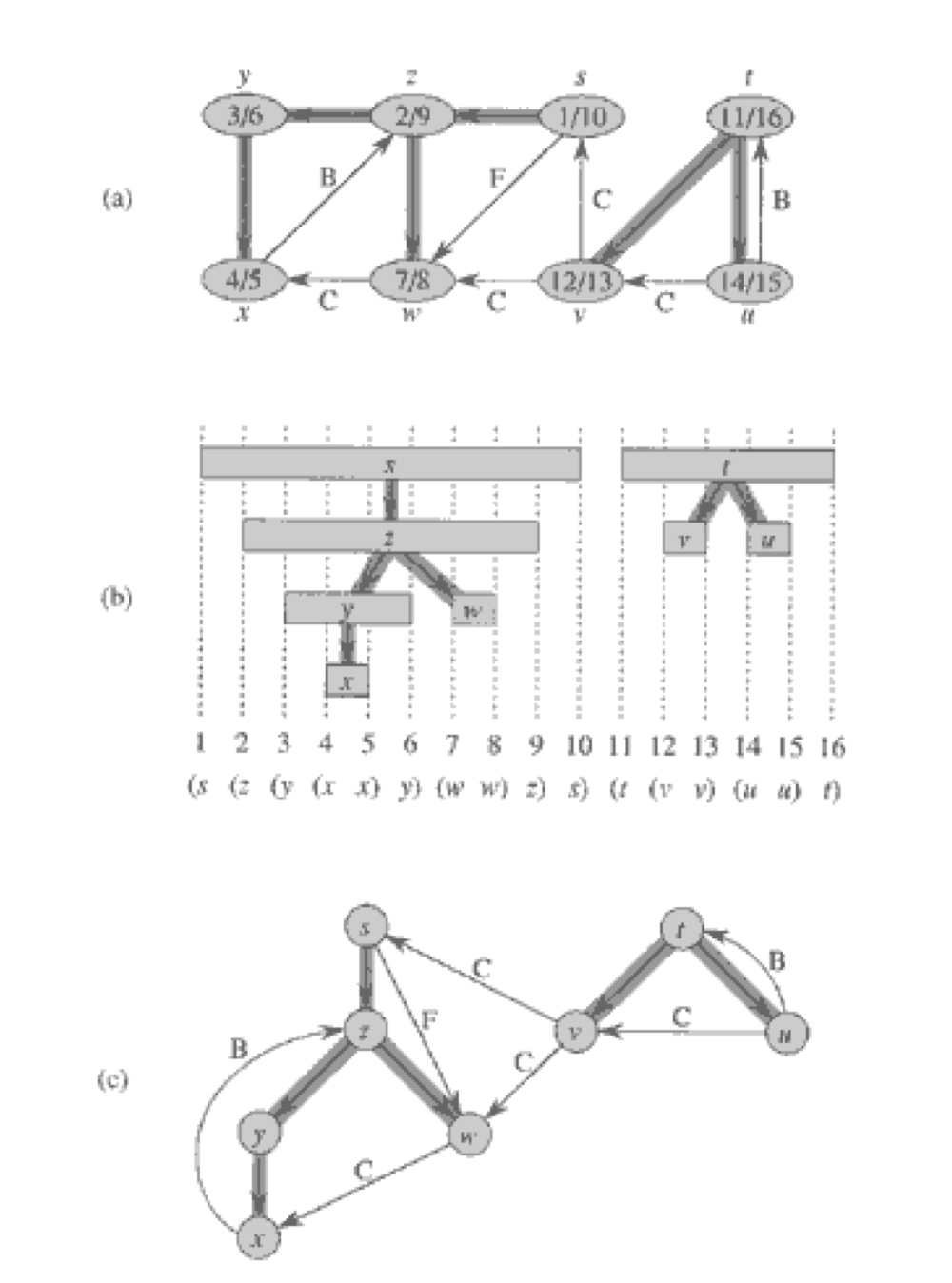
이 정리는 탐색 중 각 정점의 발견 및 종료 시간이 마치 중첩된 괄호처럼 정렬된다는 것을 나타낸다.
예시를 들자면, ()가 u의 d와 f라고 하고, []가 v의 d와 f라고 한다면, () [] ([]) [()] 의 정렬은 옳은 정렬이다.
([)] [(])는 옳지 않은 정렬이다.
또다른 이론으로 백색 경로 정리(White-path theroem)이 있다.
이는 정점 v가 정점 u의 자손이 되기 위한 조건을 다루는데, d[u]시점으로 볼 때, u에서 v까지의 경로에 백색 정점만 존재해야 한다는 것이다. 이때 u는 방금 GRAY로 색칠된 상태이다.
마지막으로, 방향성이 없는 그래프에서는 F나 C간선은 없고, 오로지 트리와 B간선만을 가진다.
** 대학교 수업을 듣고 이해한 부분을 최대한 풀어서 작성한 글입니다.
틀린 정보가 존재할 수 있으며, 언제나 피드백은 환영입니다. **
'DKU > 알고리즘 및 실습' 카테고리의 다른 글
| Minimum Spanning Trees (0) | 2024.11.20 |
|---|---|
| Elementary Graph Algorithms2 (1) | 2024.11.13 |
| Sorting in Linear Time (0) | 2024.11.01 |
| Quick Sort Algorithm (1) | 2024.10.16 |
| Heap Sort Algorithm (0) | 2024.10.16 |
