정렬 알고리즘에는 여러가지 타입이 존재한다.
정렬에는 요소들이 순차적으로 증가하게끔 만드는 오퍼레이션만 사용되며, 이는 요소의 쌍을 비교하면서 이루어진다.
Exchange Sorting - Bubble Sort, Quick Sort
Insertion Sort
Selection Sorting - Selection Sort, Heap Sort
Merge Sort
Distribution Sort - Bucket Sort, Radix Sort
정렬의 하한(lower bound)
하한은 주어진 입력을 정렬하기 위해 필요한 최소 계산 작업을 의미한다. 비교 기반 정렬 알고리즘의 경우, 이 최소 비교 횟수는 보통 $\Omega(n\lg n)$이다. 여기서 어떤 비교 기반 정렬이 수행하는 비교 과정을 추상화한 것을 결정 트리 모델이라고 한다. 특정 정렬 알고리즘이 주어진 크기의 입력에 대해 수행하는 비교 과정을 트리 구조로 나타낸 것이다. 이 모델은 제어 흐름과 데이터 이동을 추상화하여, 단순히 비교횟수를 계산하는데 집중한다.

결정 트리의 특징에 대해서 알아보자.
- 결정 트리의 리프 노드는 가능한 모든 정렬의 결과를 나타낸다. 따라서 리프는 $n!$개 이상 존재하는데, 가능한 모든 순열이 적어도 한 번은 나타나야 하기 때문이다.
- 각 n에 대해 하나의 트리가 존재하며, 이는 해당 n개의 요소를 정렬할 때 발생하는 비교 과정을 나타낸다. 트리의 각 노드는 알고리즘이 특정 시점까지 수집한 정보에 기반하여 두 개의 분기로 나뉘며, 가능한 모든 실행 경로를 모델링한다.
- 루트에서 리프까지의 가장 긴 경로, 즉 트리의 높이는 사용하는 알고리즘에 따라 달라진다. 삽입 정렬의 최악의 경우 경로 길이는 $O(n^2)$이 되고, 병합 정렬의 최악의 경우 경로 길이는 $O(n\log n)$이 되는 것이다.
- 높이가 $h$인 모든 이진 트리는 최대 $2^h$개의 리프를 가질 수 있다. 리프의 개수를 $l$, 트리의 높이를 $h$라고 할 때, $l \leq 2^h$가 성립한다.
- n개의 요소를 정렬하는 결정 트리는 높이가 $\Omega(n\lg n)$이다.
Sorting is Linear Time: 선형 시간 정렬
비교를 통해 정렬하지 않고, 입력에 대한 특정 가정을 기반으로 선형 시간에 정렬을 수행하는 방식이다.
Counting Sort: 계수 정렬
계수 정렬에는 정렬할 숫자들이 {0, 1, 2 ... k} 와 같은 범위 내의 정수여야한다.
배열 [1... n]이 주어지며, 여기서 각 요소들은 모두 {0, 1, 2 ...k} 범위 내에 속하는 정수이다. 배열 A, 요소의 개수 n, 최대 값 k가 파라미터로 주어진다. 정렬이 이루어진 후에는, 정렬된 결과를 저장한 배열 B[1...n] 이 출력된다. B는 미리 할당되어 있으며, 파라미터로 주어진다. 이 외에도 정렬 과정에서 보조적으로 사용할 배열 C[0 ... k]가 존재한다.

코드만 보면 이해가 잘 안되니, 그림과 함께 보자.

먼저 보조적으로 사용할 배열 C를 만들어준다. 이때, 배열 C의 길이는 최댓값 k만큼의 길이로 생성한다.
이제 배열A를 흝으며 해당 요소 크기의 값을 가지고 있는 배열C 인덱스의 요소 값을 증가시켜준다. 그니까 무슨 말이냐면, A배열의 8번 인덱스에 3이 있다. 그러면 C배열 3번에서 1을 증가시키는 것이다. 이것을 반복하면 그림(a)의 C배열이 완성된다.
그리고 C 배열의 0번부터 누적해서 값을 더해나간다. 0번(2)과 1번(0)을 더해서 1번에 2가 저장되었다. 1번(2)과 2번(2)을 더해서 2번에 4가 저장되었다. 이것을 반복하면 그림 (b)의 C배열이 완성된다.
여기서 배열 C의 i번째 요소가 의미하는 것은, i보다 작거나 같은 값이 그 요소의 값만큼 존재한다는 것이다. 즉, 3보다 작거나 같은 값이 총 7개 존재한다는 것이다.
이제 배열 A를 뒤에서부터 흝기 시작하며 정렬을 시작한다.
A[8]은 3이고, 이것을 C에 대입한다. C[3]은 7이고, B[7]에 3을 넣어주며 정렬을 한다. 이 때 C[3]의 값은 1 감소시켜준다.
이것을 반복하면 배열 B에서 정렬이 완성된다.
계수 정렬의 시간 복잡도는 $\Theta(n+k)$이다. 만약 $k = O(n)$일 경우, 계수 정렬의 시간 복잡도는 $\Theta(n)$이 된다.
k 값의 크기에 따라 계수 정렬의 실용성이 달라지는데, 4비트나 8비트 값에 대해서는 적합할 가능성이 있고, 16비트는 적합하지 않을 가능성이 높으며, 32비트는 적합하지 않다.
계수 정렬은 기수 정렬(radix sort)에서 부분적으로 사용되며, 계수 정렬은 안정적인 정렬 알고리즘이다. 즉, 동일한 값을 가진 숫자들이 출력 배열에서 입력 배열과 같은 순서로 나타난다. 이는 동일한 값을 가진 두 숫자 사이에서 먼저 입력 배열에 나타난 숫자가 출력 배열에서도 먼저 나타나도록 한다는 규칙에 따라 정렬된다.
Radix Sort(기수 정렬)


기수 정렬은 자릿수 별로 정렬을 하는 알고리즘이다.
각 반복 단계의 개수 i에 대한 수학적 귀납법을 사용하여 정렬의 정확성을 증명한다.
첫번째부터 i-1번째 자릿수까지는 이미 정렬되어 있다고 가정하며, i번째 자릿수에 대해 안정적인 정렬을 수행하면, 첫 번째부터 i번째 자릿수까지 정렬된 상태로 유지됨을 보여야한다.
이를 위해,
- i번째 자릿수가 다른 두 숫자의 경우, i번째 자릿수를 기준으로 정렬하면 그 순서가 올바르게 정의된다. 이때, i번째부터 i-1번째 자릿수는 관련이 없다.
- i번째 자릿수가 같은 두 숫자의 경우, 귀납적 가정에 의해 이 숫자들은 이미 올바른 순서로 되어있으므로, i번째 자릿수를 기준으로 한 안정적인 정렬은 이 숫자들의 순서를 유지한다.
n개의 d 자리 수가 주어졌을 때, 각 자리수는 최대 k개의 값을 가질 수 있다. 이 경우, 기수 정렬은 $\Theta(d(n + k))$ 시간에 이러한 숫자들을 정확하게 정렬할 수 있다. 각 자리수별로 $\Theta(n+k)$의 시간이 소요되고, d번 반복하는 것이니 전체 시간 복잡도는 $\Theta(d(n+k))$가 되는 것이다. 여기서 $k = O(n)$이라면, 시간 복잡도는 $\Theta(dn)$이 된다.
또한, n개의 b비트 자리수가 주어지고, 임의의 양의 정수 r이 b이하일 때, 기수 정렬은 $\Theta(b/r・(n + 2^r))$ 시간에 숫자들을 정확히 정렬할 수 있다. 여기서 r은 비트를 나누는 단위이며, 각 단계에서 사용할 비트 수를 의미한다.
n개의 단어에서 각 단어는 b비트를 가지고, 각 단어를 r비트로 나누면, 자릿수의 개수는 $d = \left \lceil b/r \right \rceil$이 된다. 계수 정렬을 사용하며, 이때 $k = 2^r - 1$로 각 자릿수의 범위가 정해진다.
예를 들자면, 32비트의 단어를 8비트로 나눈다면,$ b = 32, r = 8, d = \left \lceil 32/b \right \rceil = 4, k = 2^8-1 = 255 $가 된다.
그렇다면 r값은 어떻게 정하는 것일까?
b/r 와 $n + 2^r$을 균형 있게 유지하도록 r을 선택한다. 일반적으로 r = $\log n$을 선택하면, 시간 복잡도가 $\Theta(n l\log n)$에 가까워진다. 예를 들어, 32비트 숫자를 정렬할 때 r = $\log n$ = 약 16, 즉 16비트를 사용하면 d = 2가 되어 총 2번의 패스로 정렬을 완료할 수 있다.
Bucket Sort
버킷 정렬에서의 입력값은 [0, 1) 구간에서 균등하게 분포된 임의의 값으로 생성된다고 가정한다.
[0,1) 구간을 크기가 같은 n개의 버킷으로 나누고, n개의 입력값을 해당하는 버킷에 분배한다.
각 버킷들을 정렬하고, 다음 버킷을 순회하면서 각 버킷에 있는 요소들을 나열하여 최종 정렬된 결과를 얻는다.
입력에는 배열 A[1...n] 이 주어지며, 모든 요소 A[i]는 $0 \leq A[i] < 1$ 범위 내에서 존재한다.
추가로 B[0... n-1]라는 보조 배열을 사용하며, 이는 linked list로 이루어진 n개의 버킷을 저장한다.

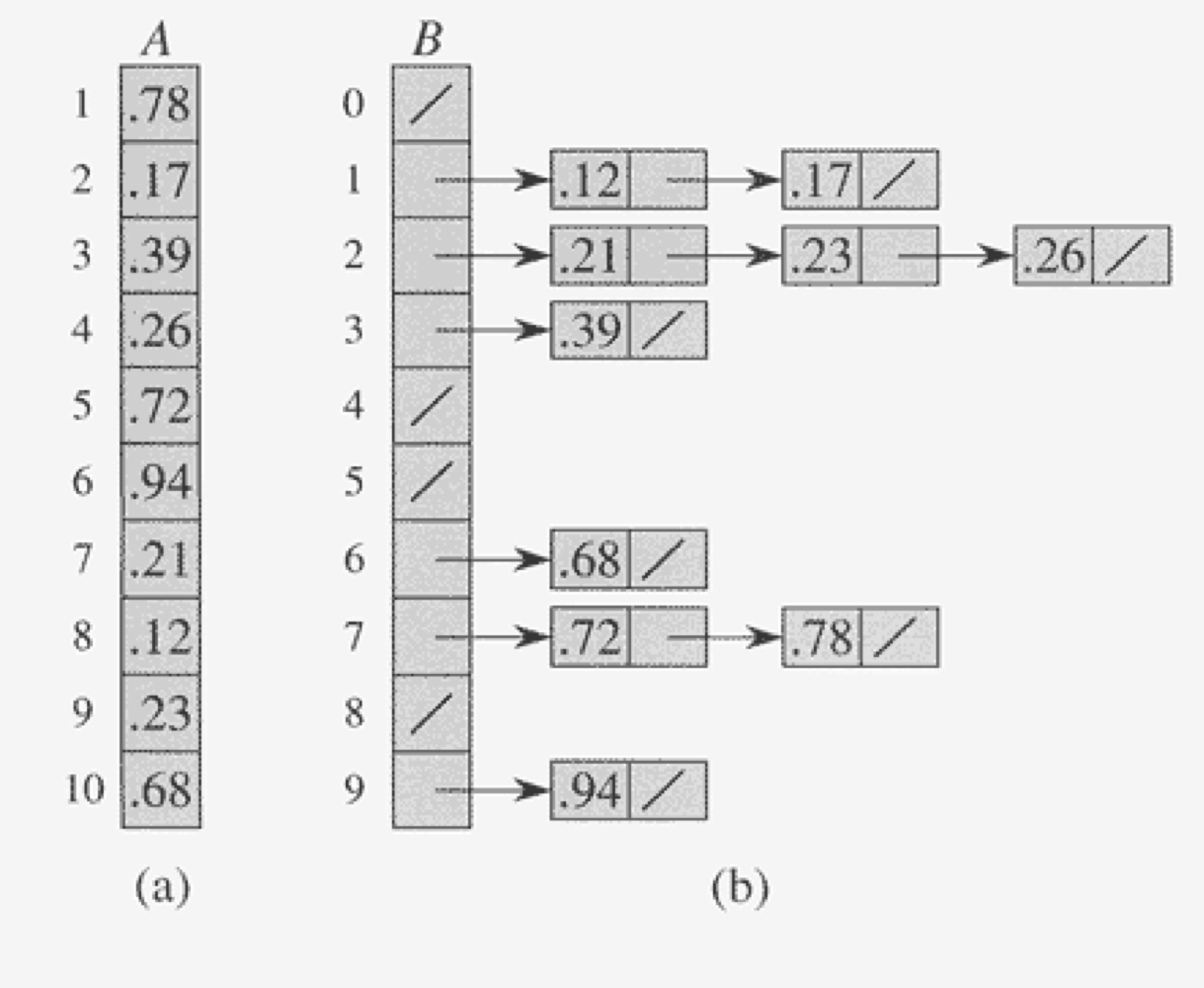
그림 (a)를 보면, 배열 A의 모든 요소는 0과 1 사이에서 존재하는 것을 알 수 있다.
배열 B는 범위에 따라서 n개의 버킷으로 나눈 후에, 범위 내에 존재하는 요소들을 받고 정렬한다.
각각 정렬된 버킷은 pointer로 연결되어 최종 정렬이 이루어진다.
만약 $A[i] \leq A[j]$이면, $\left \lfloor n・A[i]\right \rfloor \leq \left \lfloor n・A[j] \right \rfloor$이 성립한다.
같은 버킷에 삽입되는 경우에는 버킷 내에서 삽입 정렬을 통해 정렬되고, 더 낮은 버킷에 정렬되는 경우에는 각 버킷의 리스트를 순서대로 연결하면서 요소들이 올바른 순서대로 배열된다.
버킷 정렬의 시간 복잡도는 삽입정렬을 제외하고 $\Theta(n)$인데, 이는 버킷에 너무 많은 값이 들어가지 않는 가정에 의존한다.
직관적으로, 각 버킷에 일정한 수의 요소가 배정된다면, 각 버킷을 정렬하는데 $O(1)$ 시간이 소요된다. 따라서 전체 버킷을 정렬하는데 $O(n)$ 시간이 걸린다. 평균적으로 각 버킷에 요소가 하나씩 있을 것으로 예상되므로, 각 버킷의 요소 수가 적어 빠른 정렬이 가능하다는 것이다.
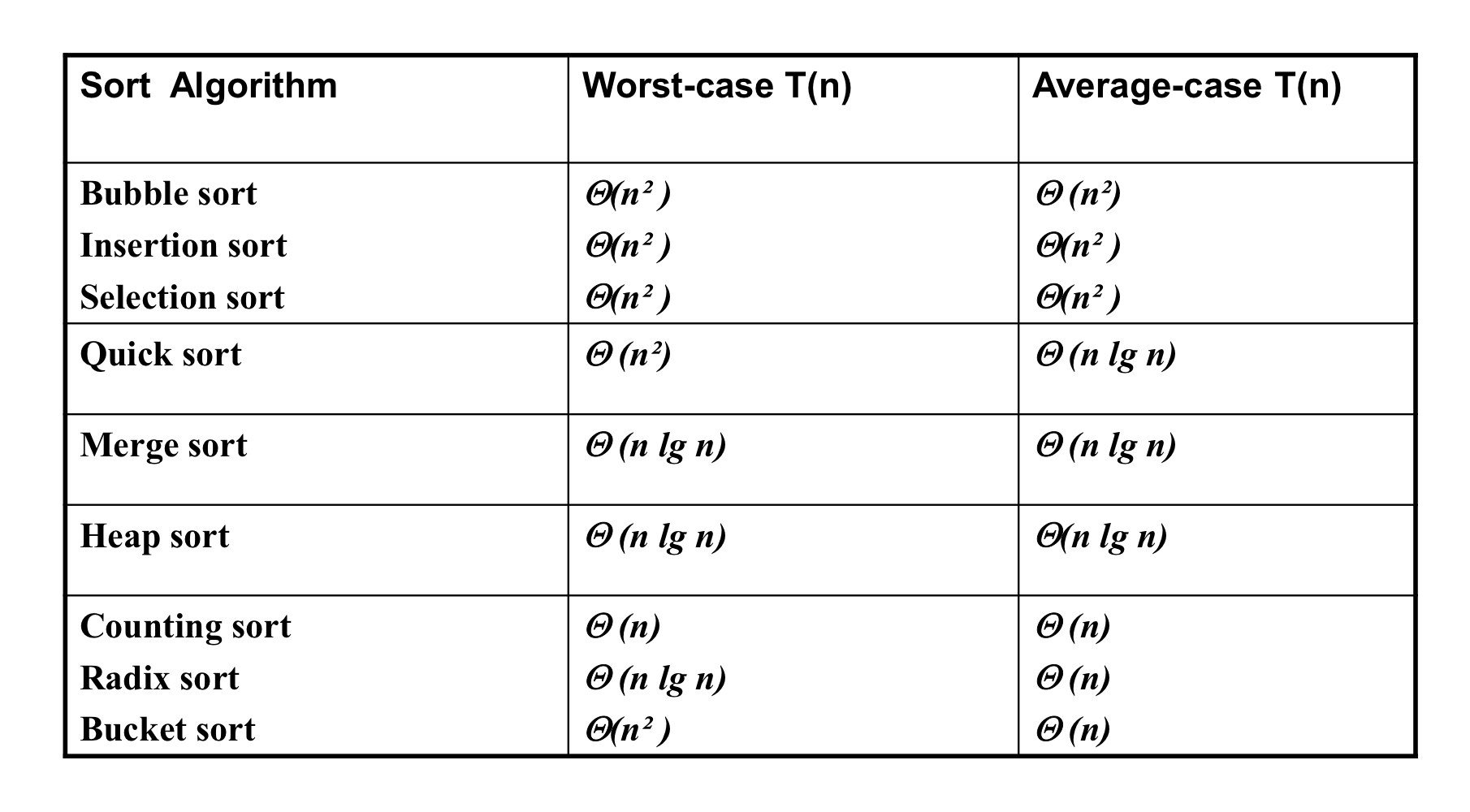
이제껏 배운 정렬 알고리즘의 시간 복잡도를 정리해놓은 사진이다.
$O(n^2)$의 시간복잡도를 가지는 알고리즘 중에서는 Bubble sort > Selection sort > Insertion sort 순으로 실행시간이 길다.
$O(n \log n)$의 시간복잡도를 가지는 알고리즘 중에서는 Heap sort > Quick sort > Merge sort 순으로 실행시간이 길다.
$O(n)$의 시간복잡도를 가지는 알고리즘 중에서는 Radix sort > Bucket sort 순으로 실행시간이 길다.
교수님이 진도가 급하셨는지 알고리즘을 휙휙휙 넘기셔서 아마 따로 공부해야될 듯 싶다.
열심히 복습한 결과가 좋은 중간고사 성적으로 돌아왔다. 넘 신낭
** 대학교 수업을 듣고 이해한 부분을 최대한 풀어서 작성한 글입니다.
틀린 정보가 존재할 수 있으며, 언제나 피드백은 환영입니다. **
'DKU > 알고리즘 및 실습' 카테고리의 다른 글
| Elementary Graph Algorithms2 (1) | 2024.11.13 |
|---|---|
| Elementary Graph Algorithms (0) | 2024.11.07 |
| Quick Sort Algorithm (1) | 2024.10.16 |
| Heap Sort Algorithm (0) | 2024.10.16 |
| Recurrences (0) | 2024.10.08 |
