Recurrences

재귀함수는 하나 이상의 기본 사례에 의해 정의되고, 더 작은 인수를 사용하여 자기 자신으로 정의되는 함수이다.

재귀함수 예시

 

---

Methods for sloving recurrences: 재귀함수를 푸는 메서드

Repeated Substitution Method(반복 치환)

 

위 재귀함수식을 어디서 많이 봤을 텐데, merge sort에서 등장했었다.

반복 치환 메서드는 말 그대로 치환을 반복하면서 식을 유도해나가는 방식이다.

 

merge sort 알고리즘은 먼저 원소가 한개 남을 때까지 배열을 쪼갠다.

$T(n) = 2T(n/2) + n$의 식을 쪼개보면,

$T(n) = 2(2T(n/2^{2}) + n/2) + n = 2^{2} T(n/2^{2}) + 2n$이다.

한번 더 쪼개보자.

$T(n) = 2^{2}(2T(n/2^{3}) + n/2^{2}) + 2n = 2^{3}T(n/2^{3}) + 3n$

 

규칙이 보이는가?

...

$T(n) = 2^{k}T(n/2^{k}) + kn$

위의 식이 더 이상 쪼개질 수 없을 때, $n/2^{k} = 1$이 될 것이다.

$n/2^{k} = 1 \rightarrow n = 2^{k} \rightarrow k = log_2^n$ 으로 바꿀 수 있다.

 

...

$T(n) = 2^{lg n}T(1) + (lg・n)n = n + n lg n$

그러므로, $$T(n) = O(n \lg{n})$$

 

The Substitution method(치환)

그냥 치환 메서드라고 써져있지만, 반복 치환과의 차이점은 추측 후에 증명을 한다는 것이다.

 

반복 치환에 사용했던 식을 다시 예시로 들겠다.

반복 치환은 식을 쪼개는 것으로 시작됬지만, 이번엔 추측을 한다.

Guess: $T(n) = O(n \lg{n})$

 

앞선 내용에 우리는 알고리즘을 증명하는 방법에 대해 배웠다. 

Proof: Prove that $T(n) \leq cn\lg{n}, for c>0$

$T(n) \leq 2(c・n/2・\lg{n/2}) + n \leftarrow 2T(n/2) + n$ 식을 대입한 것.

$\leq cn・\lg{n/2} + n$

$= cn (\lg{n}-1) + n = cn\lg{n} -cn + n$

$= cn \lg{n} - (c-1)n$

$\leq cn\lg{n} , if c\geq1$

 

그러므로, $$T(n) = O(n\lg{n})$$

추측이 맞았다!

 

The recursion-tree method(재귀 트리)

각 코드는 재귀함수 호출 집합 내 어느 한 곳에서 단일 하위 문제의 비용을 나타낸다.

트리의 각 레벨에서 발생하는 비용을 합산해 레벨별 비용을 계산하고, 모든 레벨 비용을 합산해 총 비용을 결정한다.

이런 방법은 분할 정복 알고리즘의 실행 시간을 설명하는 점화식을 해결하는데 유용하다.

이 방법으로 추측을 하고, 대입법으로 이를 증명한다.

재귀 트리 구조를 그린 후에 비용을 합산하면 점화식에 대한 직접적인 증명으로 사용할 수도 있다.

 

이번에는 $T(n) = 3T(n/4) + cn^{2}$ 재귀함수의 실행시간을 계산해보자.

재귀 트리

 

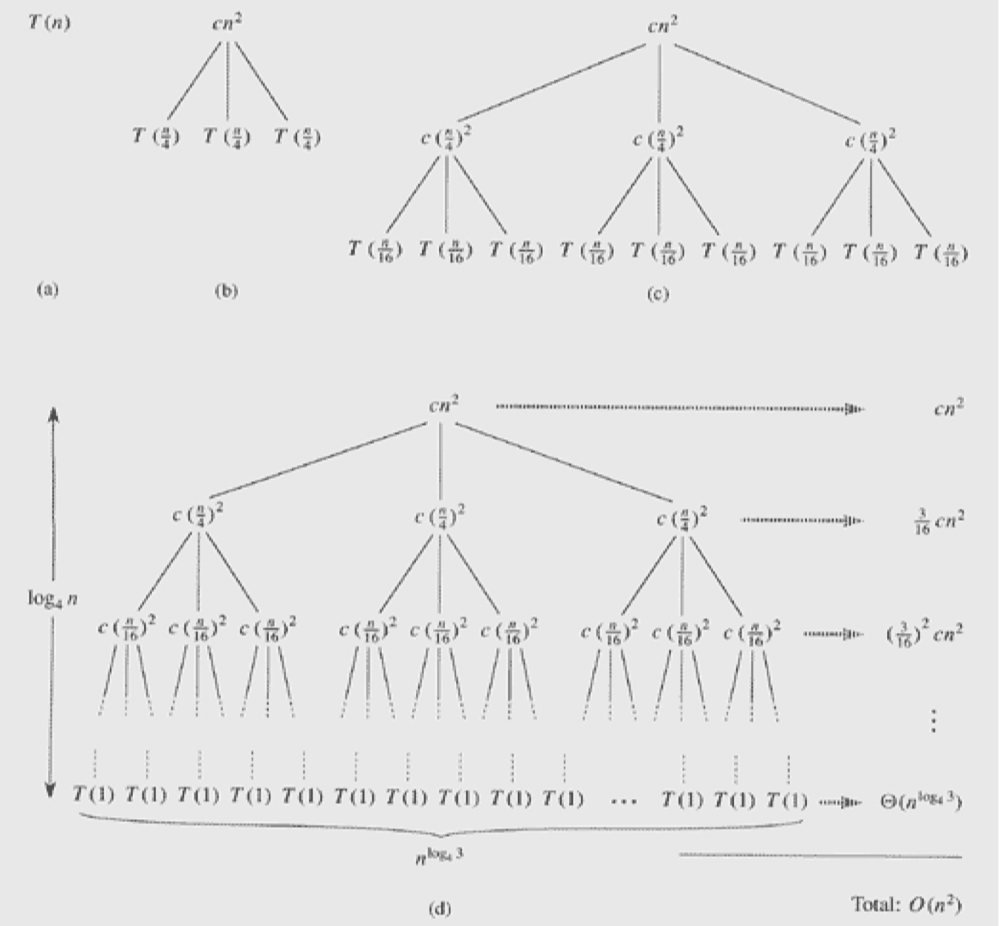
3T(n/4)라는 의미는 4조각으로 나눈 후 3조각을 병합한다는 의미이다. 나머지 1조각은 없애버린다.

트리 구조에서 높이를 구하려면, 문제가 몇개의 부분으로 나뉘는 것을 보면 된다.

위 문제는 4조각으로 나누니, 높이는 $\log_{4}{n}$이 된다.

 

다음으로 각 레벨을 살펴보니, 노드의 개수가 $3, 3^2, 3^3$... 순으로 늘어나는 것이 보인다.

k번째 레벨에서는 $3^k$개의 노드가 존재할 것이다.

 

문제의 크기가 1일 때의 노드의 개수는, 트리 구조의 높이와 연관되어 있다.

높이가 $\log_{4}{n}$이 였으니 가장 깊은 리프 노드의 개수는 $3^{\log_{4}{n}}$개가 된다.

이를 바꿔 말하면, $n^{\log_{4}{3}}$개의 노드가 된다.

문제의 크기가 1인 노드에서 발생하는 비용은 $c・1^2$, 즉 c니까 마지막 레벨의 총 비용은 $c・n^{\log_{4}{3}}$이다.

이는 $\Theta(n^{\log_{4}{3}})$ 수렴한다고 볼 수 있다.

 

이제 전체 재귀 트리의 실행 시간을 계산해보자.

레벨 k에서의 총 비용은 $3^{k} × \frac{cn^{2}}{16^{k}}$이다.

따라서 전체 실행 시간은 $T(n) = cn^2\sum_{k=0}^{\log_{4}{n}}(\frac{3}{16})^k$ 이다.

결국, $O(n^2)$이 되는 것이다.

---

 

 

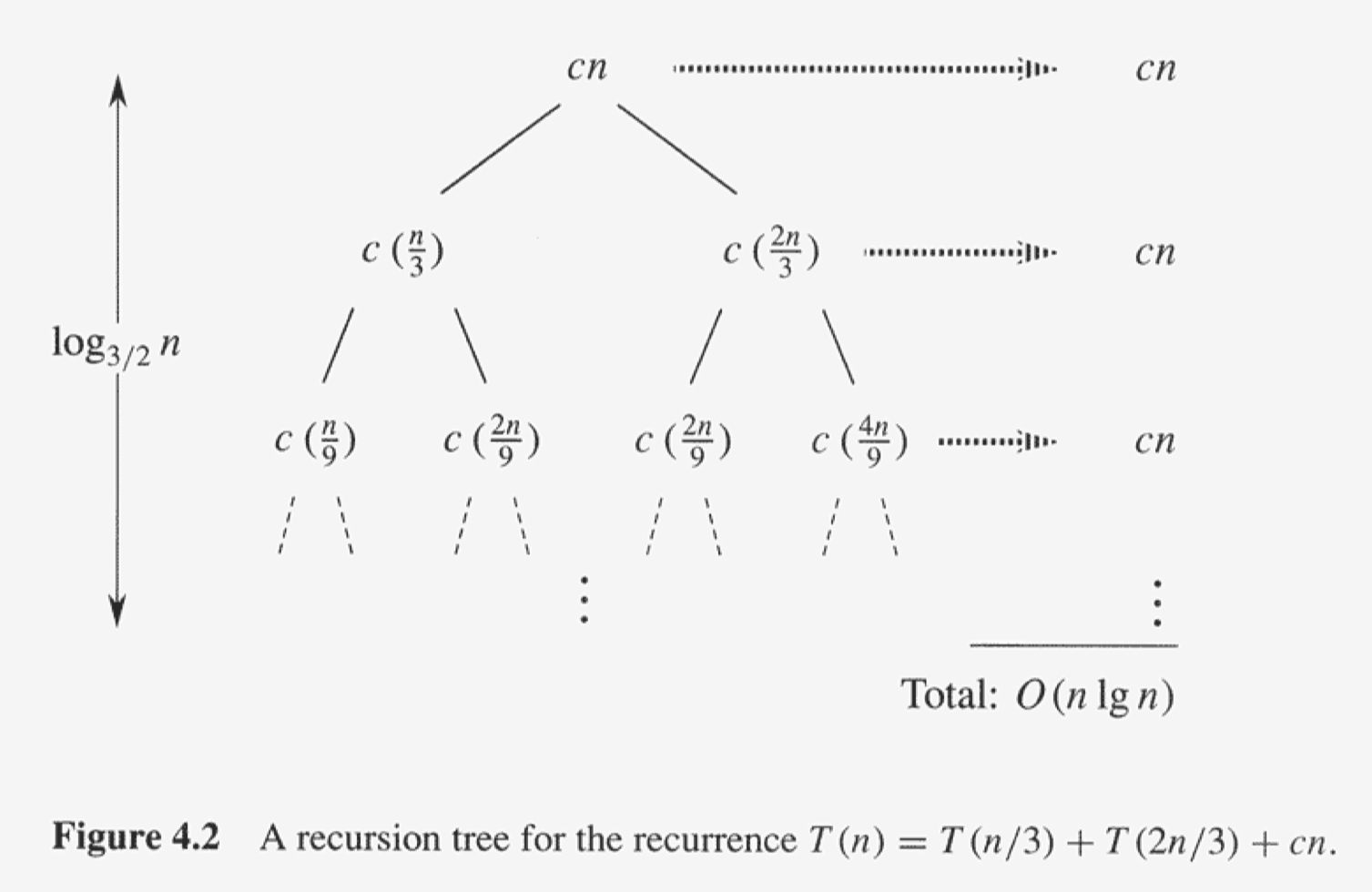
이번엔 다른 재귀 트리 구조이다. 트리의 높이는 제일 깊은 리프 노드를 기준으로 본다.

트리의 높이는 입력 크기가 1에 도달할 때까지, 즉 $(\frac{2}{3})^{k}n$ = 1 일때까지의 레벨 수 k이다.

$n = (\frac{3}{2})^k$ 이고,

높이는 $k = \log_{\frac{3}{2}}n$이 된다.

결국 트리의 높이는  $O(\log{n})$이 되고, 각 레벨에서는 $O(n)$의 비용이 발생하므로, 시간 복잡도는 $O(n\lg{n})$이 된다.

---

Master Theorem

마스터 정리는 특정한 형태의 재귀식을 빠르게 분석하여 알고리즘의 시간 복잡도를 구하는데 사용된다.

마스터 정리는 다음과 같은 형태의 재귀식을 다룬다. $$T(n) = aT(n/b) + f(n)$$

T(n)은 문제의 총 실행시간이고, a는 하위 문제의 개수이며, b는 하위 문제의 크기이다.  마지막으로 $f(n)$는 한 레벨에서 문제를 분할하고 결합하는데 드는 비용이다.

 

여기서 하위 문제를 해결하는데 드는 비용과 문제를 분할하고 결합하는데 드는 추가 비용을 비교하며 시간복잡도를 구한다.

하위 문제를 해결하는데 드는 비용은 $\log_{b}{a}$이고, 추가 비용은 $f(n)$이다.

 

case1. 하위 문제가 지배적일 때

조건: $f(n) = O(n^{\log_{b}{a-\epsilon}})$ for some $\epsilon > 0$

즉, f(n)이 하위문제를 해결하는데 드는 비용보다 작을 때를 의미한다.

하위 문제들을 재귀적으로 해결하는데 드는 비용이 더 크기 때문에, 하위 문제의 계산이 전체 시간복잡도를 지배한다.

$$T(n) = O(n^{\log_{b}{a}})$$

 

case2. 모든 레벨에서 동일한 비용일 때

조건: $f(n) = \Theta(n^{log_{b}{a}})$

이 경우에는 각 레벨에서 동일한 양의 작업이 발생하므로, 총 레벨의 수에 추가 비용 f(n)이 곱해져 시간 복잡도가 결정된다.

$$T(n) = O(n^{log_{b}{a}}\lg{n})$$

 

case3. 분할 및 병합이 지배적일 때

조건: $f(n) = \Omega(n^{\log_{b}{a+\epsilon}})$ for some $\epsilon > 0$

즉, 분할과 병합에 드는 시간이 하위문제를 해결하는데 드는 비용보다 클 때를 의미한다.

이 경우, 전체 시간 복잡도는 f(n)에 의해 지배된다.

$$T(n) = O(f(n))$$

---

** 대학교 수업을 듣고 이해한 부분을 최대한 풀어서 작성한 글입니다.

틀린 정보가 존재할 수 있으며, 언제나 피드백은 환영입니다. **