지도에서 두 지점 간의 가장 짧은 경로를 찾는 방법은 다음과 같다.
그래프에 방향과 가중치가 표현되어있다고 했을 때, 경로 p는 시작점에서 끝점으로 이어지는 정점의 순서가 된다.
w(p)는 경로 p에 포함된 간선들의 가중치 합이 된다. 이 w(p)가 최소일 때, 가장 짧은 경로라고 한다.
그래프에서 노드v에서 노드 u로 갈 수 없는 경우에는, 무한대로 표현한다.

최단 경로는 여러 개가 존재할 수 있으며, 한 노드에서 다른 모든 노드로 가는 최단 경로들은 트리 형태로 구성된다.
가중치는 경로를 따라 누적되며, 우리가 최소화해야하는 값으로 해석된다.
최단 경로 문제에는 몇가지 유형이 존재한다.
- Single-source (단일 출발점): 주어진 출발점 s에서 그래프의 모든 정점 v까지의 최단 경로를 찾는 문제
- Single-destination(단일 도착점): 모든 정점으로부터 주어진 도착점까지의 최단 경로를 찾는 문제
- Single-pair(단일 쌍): 두 정점 u와 v간의 최단 경로를 찾는 문제
- All-pairs(모든 쌍): 그래프의 모든 정점 u,v에 대해 최단 경로를 찾는 문제
위 그림을 보면 알 수 있지만, Negative-weight edge(음수 가중치 간선)도 존재한다.
음수 가중치 간선이 존재해도 괜찮지만, 음수 가중치 사이클이 출발점에서 접근 가능하지 않아야한다. 음수 가중치 사이클이 계속 반복되면 가중치가 $-\infty$로 줄어들기 때문이다. 이렇게 되면 그래프 전체에서 유효한 최단 경로를 정의할 수 없게 된다.
일부 알고리즘은 그래프에 음수 가중치 간선이 없어야만 동작하며, 음수 가중치 알고리즘을 다룰 수 있는 알고리즘이 따로 존재한다.
Optimal Substructure (최적 부분 구조)
Lemma. 최단 경로의 모든 부분 역시 최단 경로다.
Proof. 자르기와 붙이기(Cut-and-paste)로 증명 가능하다.
p가 u에서 v로 가는 최단 경로라고 가정할 때, 이 경로는 여러 부분 경로로 나눌 수 있다. $p = p_{ux}+p_{xy}+p_{yv}$
따라서, 최단 경로의 가중치는 다음과 같이 표현된다. $w(p) = w(p_{ux})+w(p_{xy})+w(p_{yv})$
만약 x에서 y로 가는 더 짧은 경로($p'_{xy}$)가 있다고 가정한다면, 새로운 경로 $p' = p_{ux}+p_{x'y}+p_{yv}$가 만들어진다.
이 새로운 경로의 가중치는 최단 경로 가중치보다 작아진다. $w(p') < w(p)$
이는 p가 최단 경로라는 가정가 모순되며, x에서 y로의 부분 경로 역시 최단 경로여야한다.
Cycles
최단 경로는 사이클을 포함하지 않는다.
음수 가중치 사이클은 위에서 설명했듯이 이미 배제되었다. 양수 가중치 사이클을 포함하면 경로 가중치가 증가하므로, 사이클을 생략하면 더 짧은 경로를 얻을 수 있기 때문에 배제된다. 0 가중치 사이클은 포함하더라도 경로 가중치에 영향을 주지 않으므로 사용할 이유가 없다.
Output of single-source shortest-path algorithm
각 정점 v에 대해, d[v]는 출발점 s에서 정점 v까지의 최단 경로 추정값이다.
초기값의 d[v]는 $\infity$로 초기화하며, 알고리즘이 진행됨에 따라 d[v]는 감소하고 항상 $d[v] \geq \delta(s,v)$를 만족한다. 여기서 $\delta(s,v)$는 실제 최단 경로 가중치다.
$\pi[v]$는 정점 v의 최단 경로 상에서의 직전 정점(predecessor)이다.
$\pi[v]$를 통해 최단 경로의 재구성이 가능하며, 초기값은 NIL(아직 경로가 없는 상태)로 초기화된다. $\pi[v]$는 최단 경로 트리를 유도한다.
Initialization
최단 경로 알고리즘의 모든 변형은 공통적으로 INIT-SINGLE-SOURCE라는 초기화 단계를 사용하여 시작한다.

Relaxing an edge (u, v)
간선 완화는, 정점 u에서 정점 v로 연결된 간선(u,v)를 통해, 정점 v까지의 최단 경로 추정값(d[v])을 개선할 수 있는지 확인한다.
만약 d[v]를 개선할 수 있다면, d[v]를 갱신하고 v로 가는 최단 경로 상의 이전 정점 ($\pi[v]$)도 업데이트한다.


모든 단일 출발점 최단 경로 알고리즘은 INIT-SINGLE-SOURCE 호출과, 간선 완화 호출의 단계를 따른다.
알고리즘들은 간선을 완화하는 순서와 간선을 완화하는 횟수에서 차이를 보인다.
Shortest-paths Properties: 최단 경로의 특성
- 기본 원칙: INIT-SINGLE-SOURCE를 한 번 호출한 후, RELAX를 0회 이상 호출하는 것에 기반한다.
- Triangle Inequality(삼각 부등식): 모든 간선 (u, v)에 대해 $\delta(s,v) \leq \delta(s, u) + w(u, v)$
- Upper-bound Property(상한 속성): 항상 $d[v]\leq\delta(s,v)$를 만족한다. 한번 $d[v] = \delta(s,v)$가 되면, 이후 값은 더 이상 변하지 않는다.
- No-path Proerty(경로 없음 속성): $\delta(s,v) = \infty$이면, $d[v]=\infty$를 항상 유지한다. s에서 v로 가는 경로가 없는 경우, d[v]는 무한대라는 것이다.
- Convergence Property(수렴 속성): 만약 u→v가 최단 경로의 일부이고, $d[u] = \delta(s, u)$라면, RELAX(u, v, w)를 호출한 후 $d[v] = \delta(s,v)$가 된다.
- Path Relaxation Property(경로 완화 속성): 최단 경로 p가 주어졌을 때, 간선을 순서대로 완화하면 $d[v_k] = \delta(s, v_k)$이다.
Triangle Inequality
Proof. 최단 경로의 가중치는 어떠한 경로의 가중치보다 작거나 같고, u→v로 가는 경로는 s→u→v 라는 경로를 포함한다.
만약 최단 경로를 사용하면, 그 가중치는 $\delta(s,u) + w(u,v)$가 된다. 따라서 삼각 부등식이 성립한다.
Upper-bound Property
Proof. 초기 상태에서는 이미 $d[v] = \infty \geq \delta(s, v)$로 성립한다.
$d[v] < \delta(s, v)$인 정점 v가 존재한다고 가정해보자. u를 d[v]값을 변경시킨 정점이라고 하면, d[v] = d[u] + w(u, v)가 된다.
그러므로, 삼각 부등식을 식에 넣어본다면, $d[v] < \delta(s, v) \leq \delta(s, u) + w(u, v)$가 된다.
이는 $d[v] < d[u]+w(u, v)$이고, $d[v] = d[u] + w(u,v)$에 모순된다.
$d[v] = \delta(s,v)$에 도달하면, 이 값은 절대 증가하지 않는다.
RELAX 연산은 최단 경로 추정값을 낮추는 작업만 수행하므로, d[v]는 더 이상 증가하지 않는 것이다.
No-path Property
Proof. 초기화 시 $d[v] \geq \delta(s, v)=\infty$ . 따라서 d[v] = $\infty$
Convergence Property
Proof. RELAX 후 $d[v] \leq d[u] +w(u, v)$가 된다. 이는 최적 부분 구조에 따라 $d[v] \leq \delta(s, u)+w(u,v) = \delta(s, v)$가 된다. 따라서 $d[v] \leq \delta(s,v)$가 되는데 $d[v] \geq \delta(s, v)$이므로, $d[v]=\delta(s, v)$가 된다.
Path Relaxation Property
Proof. 귀납법을 사용하여 $d[v_i] = \delta(s, v_i)$임을 보인다.
초기 상태에서 $d[v_0] = 0 = \delta(s, v_0) = \delta(s, s)$이므로 성립한다.
$d[v_{i-1}] = \delta(s, v_{i-1})$가 이미 성립한다고 가정하고, 간선 완화를 진행한다.
수렴 속성에 따라 $d[v_i] = d[v_{i-1}]+w(v_{i-1}, v_i)$가 되고, d[v_i] = \delta(s, v_{i-1})+w(v_{i-1}, v_i)가 된다.
최적 부분 구조에 의해 $\delta(s, v_i) = \delta(s, v_{i-1})+w(v_{i-1}, v_i)$ 가 된다.
이는 $d[v_i] = \delta(s, v_i)$가 성립한다.
The Bellman-Ford Algorithm
벨만 포드 알고리즘은 음수 가중치 간선을 허용한다.
s에서 접근 가능한 음수 가중치 사이클이 없는 경우, TRUE를 반환하고, 음수 가중치 사이클이 있는 경우에는 FALSE를 반환한다.

첫 번째 for 루프는 그래프의 모든 간선을 |V|-1번 완화한다.
시간 복잡도는 $\Theta(VE)$이다.
각 반복 단계에서 얻는 값은 간선 완화의 순서에 따라 달라진다. 하지만, 음수 가중치 사이클이 없다고 가정하면 |V|-1 번의 반복 후에 반드시 수렴한다.
Proof. v가 s에서 도달 가능한 정점이고, p가 최단 경로라고 가정한다. p는 사이클이 없는 경로이므로, 간선의 수는 $k \leq|V|-1$이다.
루프는 (v0, v1)을 완화하고, (v1, v2)를 완화, ... , 마지막 간선(v_{k-1}, v_k)를 완화하는 반복으로 동작한다.
경로 완화 속성으로 인해 $d[v_k] = \delta(s, v_k)$이고, 여기서 v_k = v이므로 $d[v] = \delta(s, v)$가 된다.
음수 가중치 사이클이 없는 경우, 알고리즘 종료시 모든 간선에 대해 $d[v] = \delta(s, v) \leq \delta(s, u) +w(u,v)$ = d[u] + w(u, v) 이므로, 최단 경로값과 실제 값이 동일해진다. 따라서, 벨만 포드 알고리즘은 TRUE를 반환한다.
음수 가중치 사이클(c)이 있는 경우, 벨만 포드 알고리즘이 TRUE를 반환한다고 가정해보자. 즉, 모든 간선에 대해 $d[v_i] \leq d[v_{i-1}] + w(v_{i-1} + v_i)$가 성립하는 것이다. 하지만 사이클 c를 따라가며 가중치를 합산해보면 음수가 나온다.
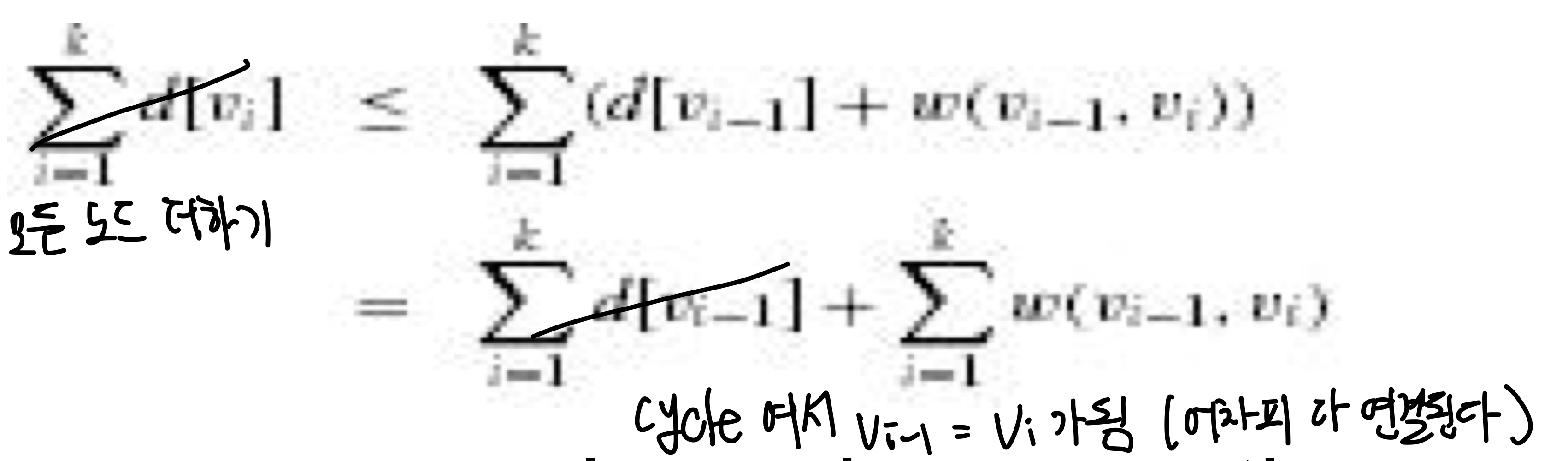
이는 벨만 포드 알고리즘이 수렴했다고 가정한 것과 모순이 되므로, FALSE를 반환한다.
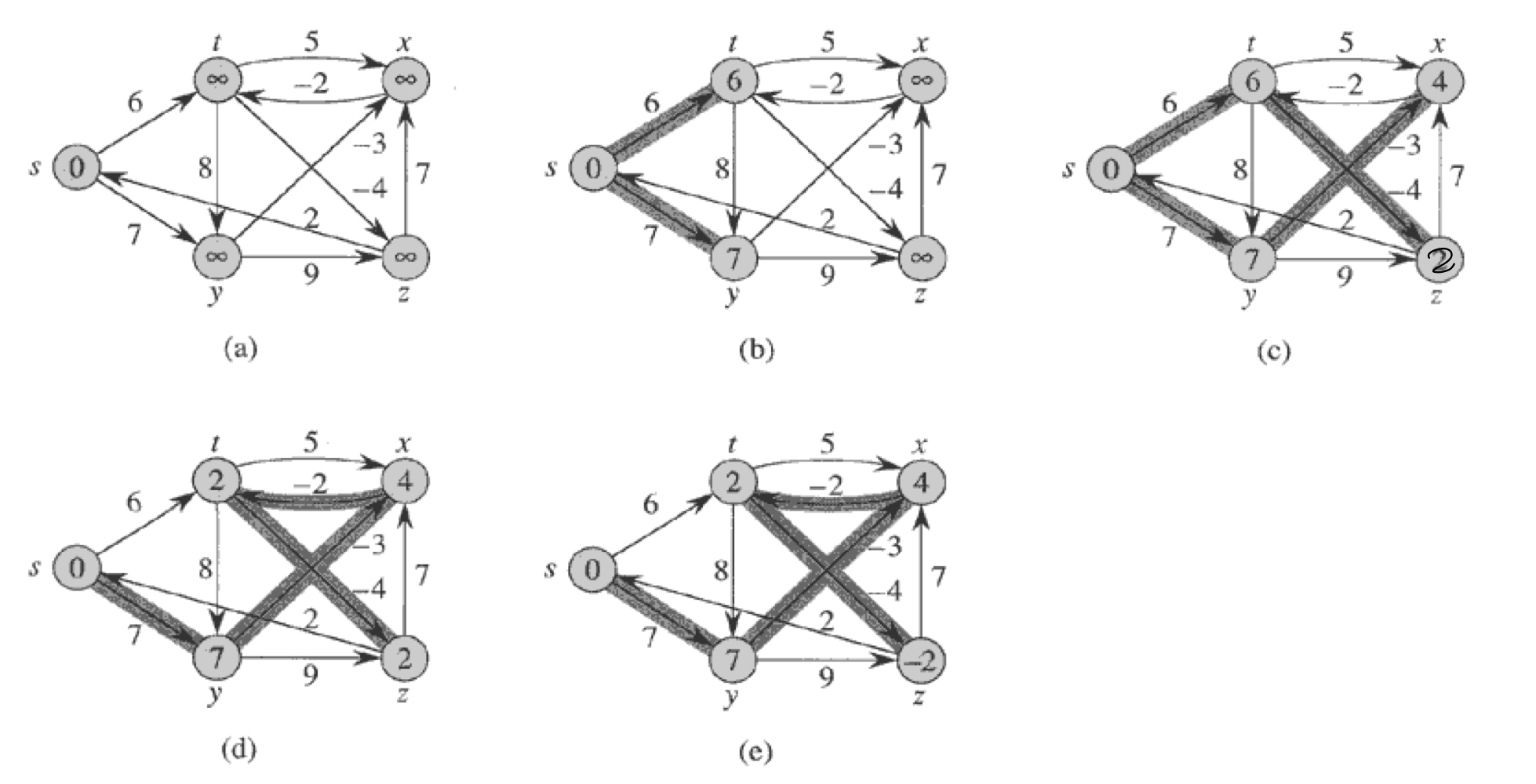
Single-source shortest paths in a directed acyclic path (DAG)
DAG이기 때문에, 음수 가중치 사이클이 존재하지 않음이 보장된다.

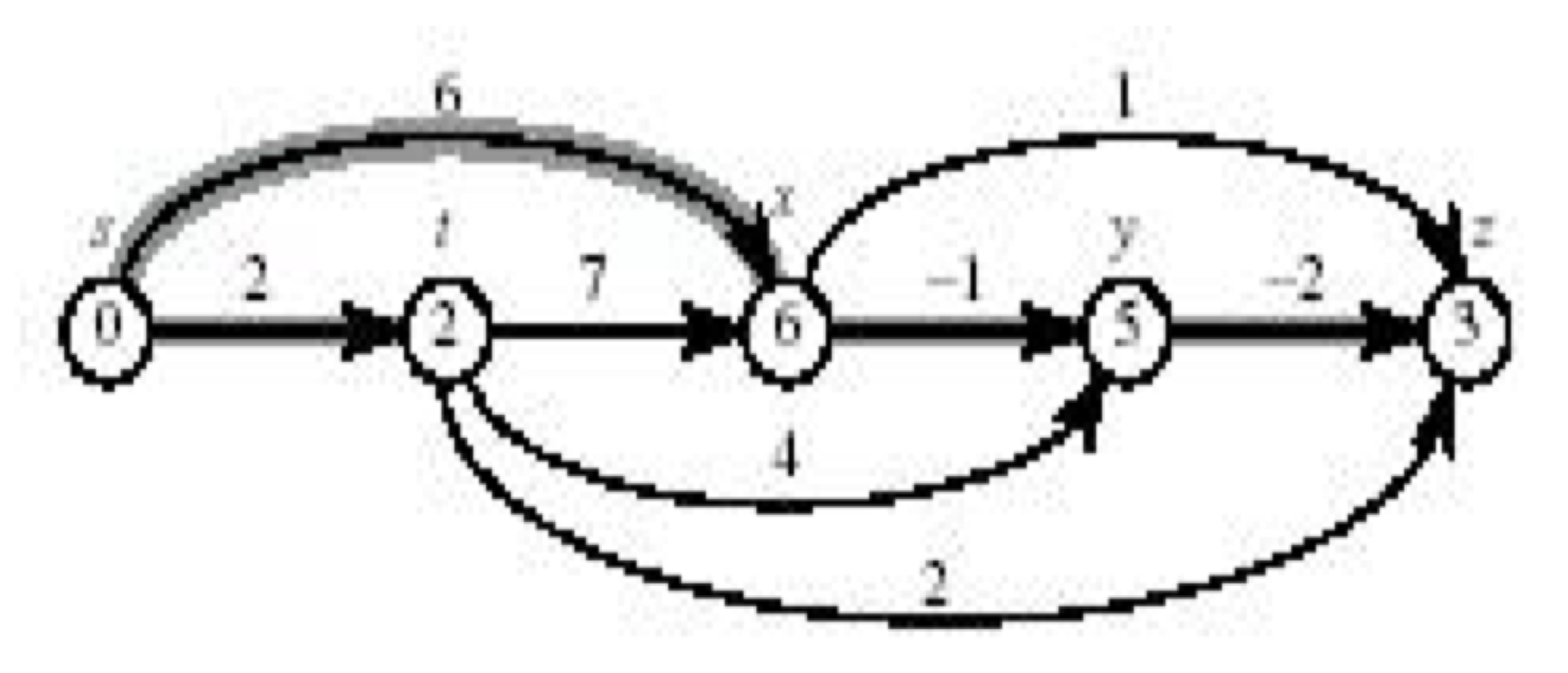
1번줄의 topologically sort을 수행하면, G의 노드가 정렬된다. 노드에 임의의 순서를 제공하면, 그래프의 처리가 가능하다.
시간 복잡도는 2번줄의 위상 정렬 시간과 4-5번 줄 for루프의 모든 간선을 한번씩 확인하며 relax 작업을 수행하는 시간을 더해, $\Theta(V + E)$가 된다.
위상 정렬 순서에 따라 노드를 처리하기 때문에, 경로 상의 간선들이 등장 순서대로 완화된다. 즉, 최단 경로 상의 모든 간선이 올바른 순서로 완화된다. 경로 완화 속성으로 인해, 최단 경로 계산히 정확히 이루어지게 된다.
DAG 그래프의 위상 정렬은 모든 노드의 선형적 정렬로, 그래프에 간선 (u, v)가 있다면 u가 v보다 순서상 앞에 위치하는 정렬이다. 그래프가 순환 그래프라면, 선형 정렬은 불가능이다.
위상 정렬은 그래프의 노드를 수평선 상에 정렬한 모습으로 볼 수 있으며, 이때 모든 유향 간선은 왼쪽에서 오른쪽으로 향하게 된다.
위상 정렬은 일반적인 정렬 방식과는 다르며, 그래프의 구조적 관계를 고려한 정렬이다.
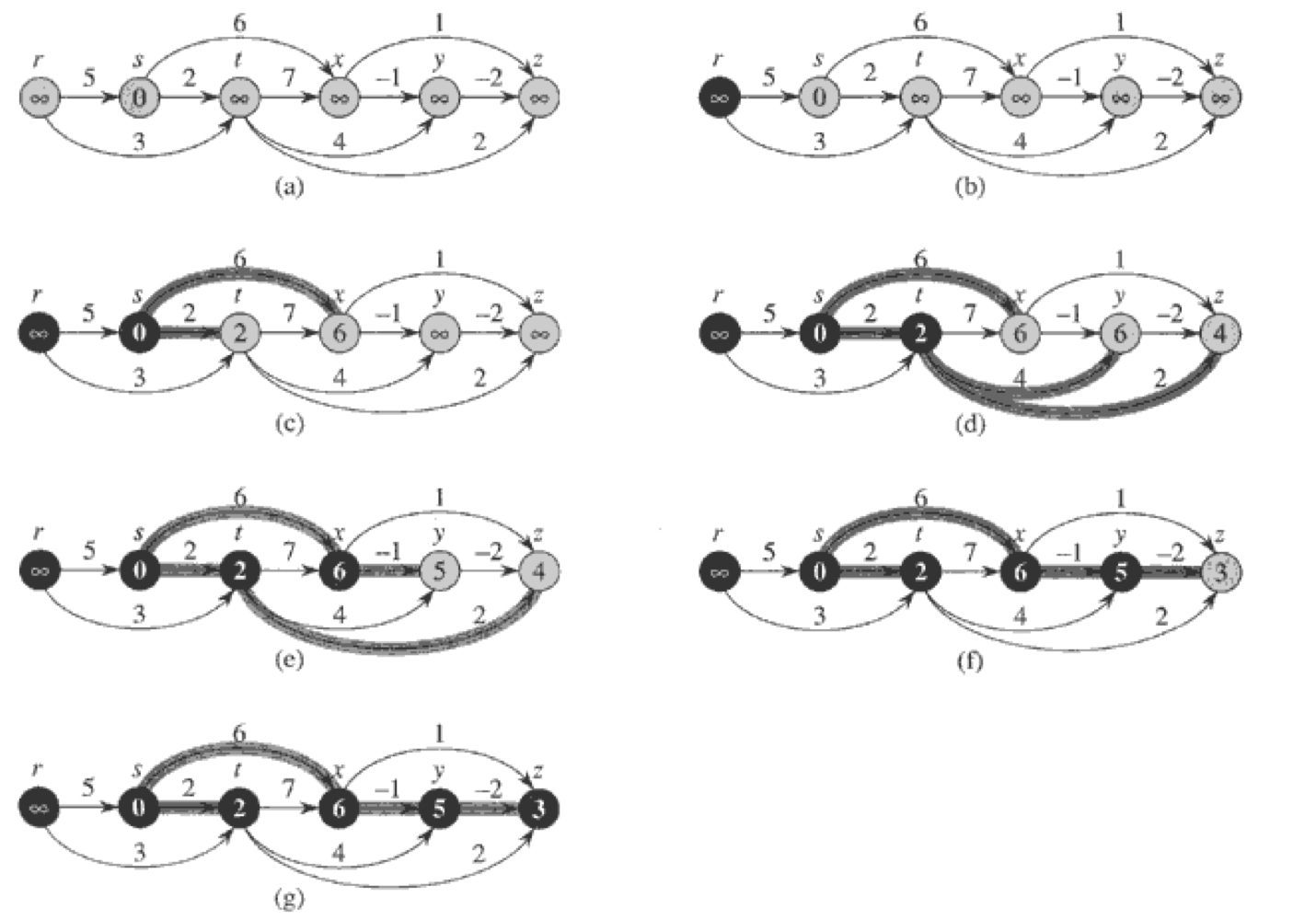
위 예시에서 노드들은 위상 정렬되어있다. 시작 노드는 s이고, d값들은 노드에 적혀져있으며, 그림자 진 간선들은 $\pi$값을 표현한다.
(a) 3-5번줄의 for 루프를 실행하기 전, 초기화된 그래프다.
(b)~(g) for루프를 실행한 이후의 그래프다. 각 반복에서 새롭게 생긴 검은색 노드는 그 반복에서 u로 사용된 노드이다. (g)에서 노드에 쓰여진 값들이 최종적인 값들이다.
Dijkstra's Algorith
다익스트라 알고리즘은 음수 가중치 간선이 없는 경우에만 사용 가능하며, 너비우선탐색(BFS)의 가중치 버전으로 볼 수 있다.
다만, FIFO 큐 대신 Priority 큐를 사용하며, 우선순위 큐의 키는 최단 경로 가중치 d[v]를 나타낸다.
알고리즘은 두 개의 정점 집합 S(최단 경로 가중치가 확정된 정점들), Q(= V-S, 아직 확정되지 않은 정점들로 구성된 우선순위 큐)을 유지한다.

다익스트라 알고리즘 역시 그래프의 초기화를 진행한 후에 시작된다. S는 공집합으로 시작하며, Q는 모든 정점으로 초기화된다.
while문은 Q가 비어있지 않을 때까지 반복되며, Q에서 가장 가벼운 정점을 선택하고 선택된 정점을 S에 추가한다.
그리고 u의 모든 인접 정점(v)에 대해 RELAX를 수행한다. RELAX를 수행하면 convergence proporty로 인해 $\delta(s, v)$가 된다.
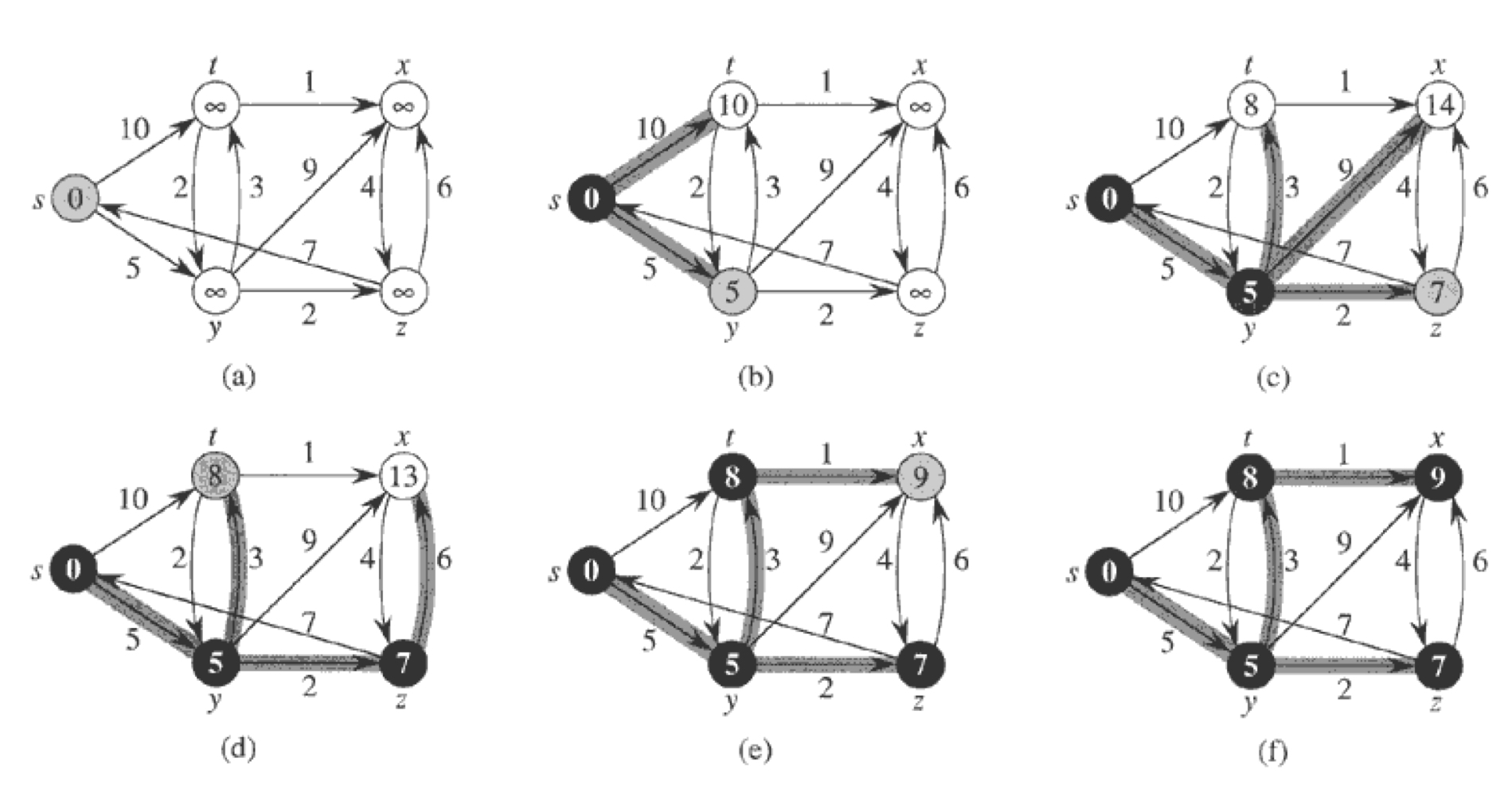
위 사진에서,
검은 노드들은 집합 S에 들어가있는 노드들이고, 흰색 노드들은 min-priority queue에 들어가 있는 노드들이다. 그림자 진 노드들은 가장 작은 d값을 가진 노드이기 때문에, 코드 5번줄에서 u로 선택된다.
while 루프를 반복 수행하면 최종적으로 (f) 그림처럼 최단 거리를 찾을 수 있게 된다.
MST의 가중치를 계산하는 Prim 알고리즘과 구조가 유사하지만, 다익스트라는 최단 경로 가중치 d[v]를 계산한다.
다익스트라 알고리즘은 Greedy 접근법으로 작동하는데, 항상 Q에서 가장 가벼운 정점을 선택하여 S에 추가한다. 이를 통해 최단 경로를 점진적으로 구축한다.
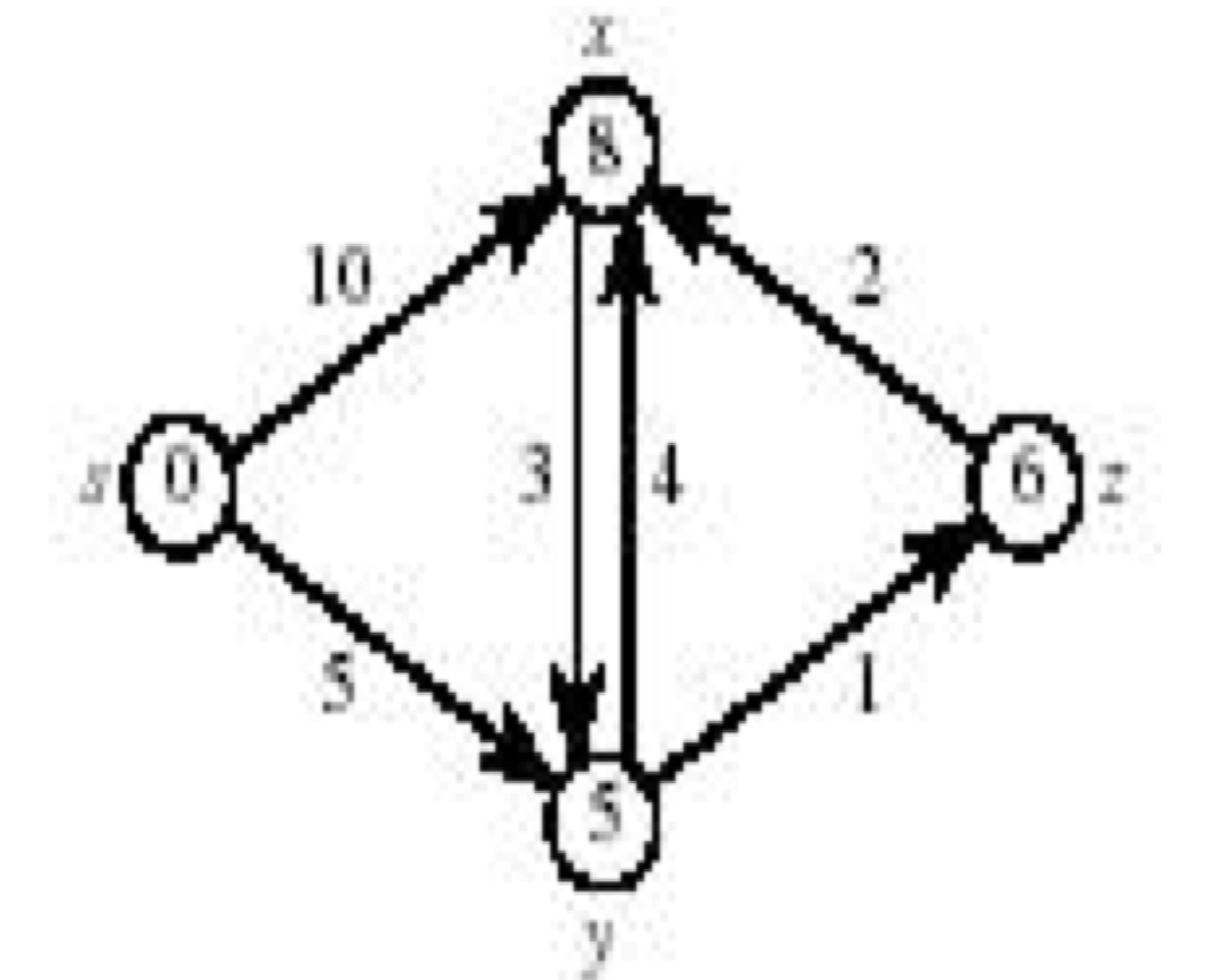
위 그림에서 S에 추가되는 순서는 s, y, z, x가 되어야한다. 정확성을 증명해보자.
루프 불변 조건을 따르면, while루프의 각 반복이 시작될 때, $d[v] = \delta(s, v)$는 $v\inS$에 대해 항상 성립한다.
- 초기화: S = 0 이므로, 당연히 조건이 성립한다.
- 종료: 루프 종료 시, Q =0이므로 S = V이다. 따라서 모든 정점 v에 대해 $d[v] = \delta(s, v)$가 성립한다.
- 유지: 각 반복에서, u가 S에 추가될 때 $d[u]=\delta(s,u)$임을 보여야한다. 반증법을 사용해보자. $d[u] \neq \delta(s,u)$인 처음으로 발생한 정점이 u라고 가정한다. $d[s]=\detla(s,s)$이기 때문에 u=s일 수가 없다. 그리고 s가 먼저 S에 추가되기 때문에 S는 비어있는 집합일 수 없다. 따라서 s→u의 경로는 존재해야한다. 만약 경로가 존재하지 않는다면, No-path property에 의해 $d[u]= \delta(s, u) =\infty$가 되어야하므로 모순이다. 즉, s→u로의 경로가 존재함은 s→u로의 최단 경로 역시 존재한다는 의미이다.
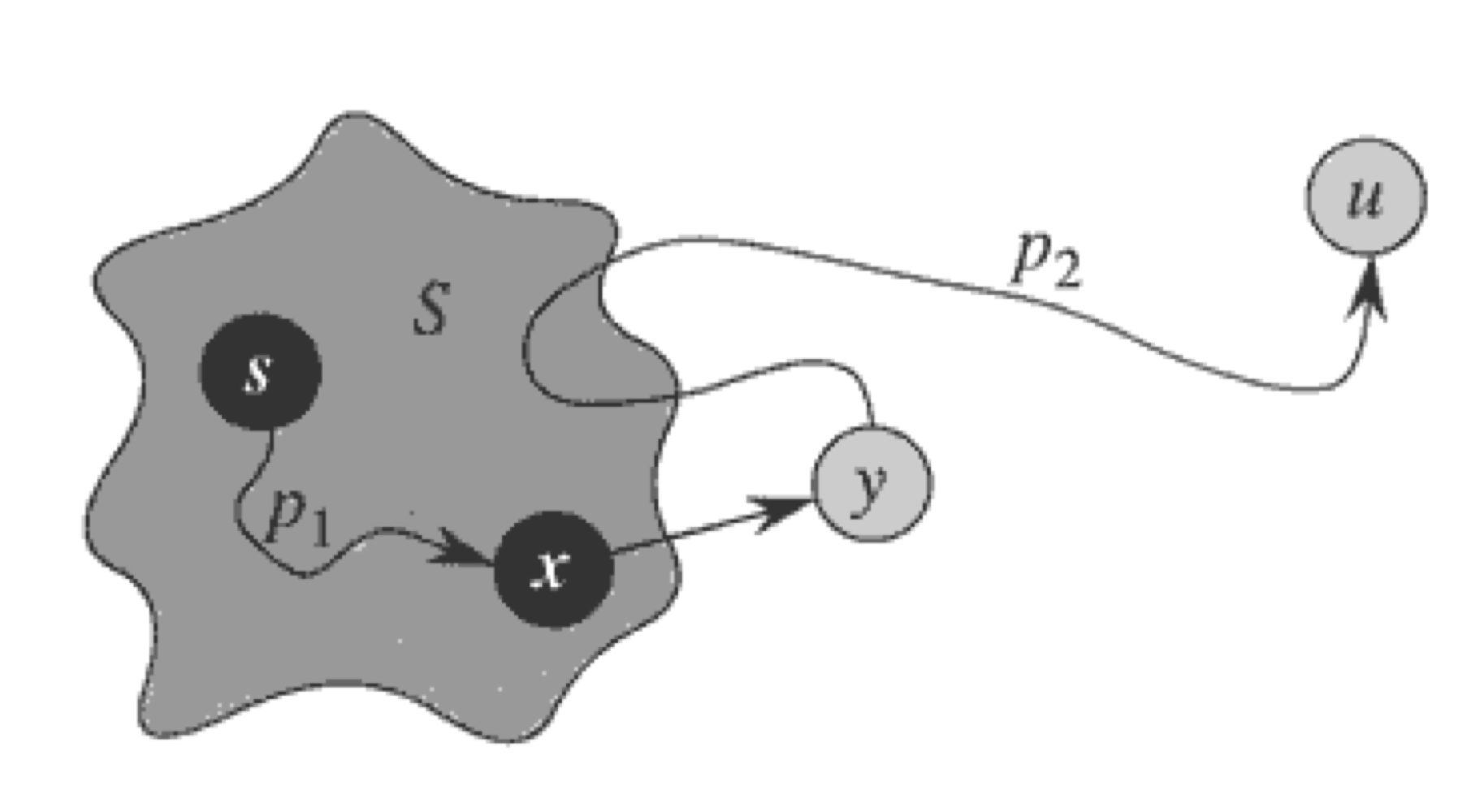
u가 S에 추가되기 직전, 경로 p는 S에 있는 정점에서 V - S에 있는 정점까지 연결되어 있다.
p에서 V - S에 속하는 첫 번째 정점을 y, 그리고 그 이전 정점을 $x \in S$라고 하자.
그러면 경로 p는 다음과 같이 나눌 수 있다.
- p1: s에서 x까지의 경로 (x=s인 경우, 간선이 없을 수 있음)
- p2: x에서 y까지의 경로 (y=u인 경우, 간선이 없을 수 있음)
Claim. u가 S에 추가될 때, $d[y] = \delta(s, y)$이다.
Proof. x가 S에 추가될 때, $d[x] = \delta(s, x)$임이 보장된다. 그 시점에서 (x, y)를 완화하므로, Convergence Property에 의해 $d[y] = \delta(s, y)$가 된다.
모순을 도출해보자. $d[u] \neq\delta(s, u)$ 이라고 가정한다.
y는 s에서 u로 가는 최단 경로에 있는 정점이다. 따라서, 모든 간선 가중치가 음수가 아니므로 $\delta(s,y)\leq\delta(s,u)$ → $d[y] = \delta(s,y) \leq \delta(s,u)$가 된다. 여기서 Upper-bound Property 에 의해 $\delta(s,u) \leq d[u]$이고, $d[y] \leq d[u]$가 된다.
y와 u는 모두 Q에 존재하고, u가 선택되었다는 건 $d[u] \leq d[u]$인 것이고, 두 조건을 모두 만족하려면 $d[y] = d[u]$일 수밖에 없다. 이는 위에서 가정한 사실과 모순된다.
다익스트라 알고리즘의 시간 복잡도는 우선순위 큐의 구현 방식에 따라 달라진다.
Binary heap을 사용하는 경우, 각 연산 (EXTRACT-MIN 및 decrease-key)은 $O(\lg V)$시간을 갖는다.
- 모든 정점에 대해 EXTRAXT-MIN 연산이 $O(V\log V)$의 시간을 갖는다.
- 모든 간선에 대해 dexrease-key 연산이 $O(E\log V)$의 시간을 갖는다.
- 따라서 총 시간 복잡도는 $O((V+E)\log V)$이 된다.
- 만약 모든 정점이 출발점에서 도달 가능하다면, $E \geq V -1$이므로 $O(E \log V)$가 된다.
** 대학교 수업을 듣고 이해한 부분을 최대한 풀어서 작성한 글입니다.
틀린 정보가 존재할 수 있으며, 언제나 피드백은 환영입니다. **
'DKU > 알고리즘 및 실습' 카테고리의 다른 글
| Greedy Algorithms (0) | 2024.12.04 |
|---|---|
| Hash Tables (0) | 2024.12.04 |
| Minimum Spanning Trees (0) | 2024.11.20 |
| Elementary Graph Algorithms2 (1) | 2024.11.13 |
| Elementary Graph Algorithms (0) | 2024.11.07 |
