최적의 값을 찾기 위해서는 실행시간이 오래걸린다.
하지만 실행시간을 줄이면, 최적의 값을 찾을 수 없게 된다. 대신 근사치(Approximation)를 찾는다.
근사치를 찾는 기법에는 Greedy Algorithm과 Dynamic Programming이 있다.
Greedy 알고리즘은 선택을 해야 할 때, 현재 순간에서 가장 좋아보이는 선택을 한다.
즉, 지역적으로 최적(locally optimal)인 선택을 하여 전역적으로 최적(globally optimal)인 해를 구하고자한다. (Greedy-choice property)
탐욕 알고리즘이 항상 최적의 해를 보장하는 것은 아니지만, 특정 문제에서는 최적 해를 최단 경로 알고리즘보다 더 빨리 구할 수 있다.
탐욕 알고리즘의 가장 대표적인 알고리즘이 MST이다.
MST의 각 safe edge는 locally optimal이고, 그 간선들은 모두 연결한 safe edge는 globally optimal이다.

매트로이드 $M = (S, I)$는 다음 조건을 만족하는 순서쌍이다.
1. S는 유한하고 비어 있지 않은 집합이다.
2. I는 S의 부분 집합들로 이루어진 비어 있지 않은 집합이며, 이를 S의 독립 집합 이라고 한다.
만약 $B \in I$이고, $A\subseteqB$라면, $A \in I$이다. 이러한 성질을 유전적 성질이라고 하며, 비어 있는 집합은 반드시 I의 원소에 포함된다.
3. $A \in I, B\in I$이고 |A| < |B|라면, $x \in B-A$인 원소가 존재하여 $A\cup x in I$가 성립한다.


Matroid 구조를 가지는 문제들은 Greedy Algorithm으로 optimal solution을 구할 수 있다.
Matroid란, MST에서 safe edge를 더해 가듯이, 가중치 또는 선정된 함수 값에 의해 구해지는 safe element를 단계별로 더해갈 때 optimal solution에 도달하는 구조를 가진 집합이다. 이를 family 라고도 하며, 부분집합의 집합이다.
Greedy for knapsack problem
배낭 문제는 탐욕 알고리즘 적용의 차이를 보여주는 좋은 예이다.
- 0-1 knapsack problem: 탐욕 알고리즘으로 해결할 수 없다. n개의 물건이 있고, 물건 i의 가치는 $v_i$d이며 무게는 $w_i$이다. 총 무게가 W 이하가 되도록 하면서 가장 높은 가치를 가지는 물건의 부분 집합을 찾는 문제다. 여기서 물건을 전제로 취하거나(1), 취하지 않거나(0) 해야하며, 부분적으로 나눌 수 없다.
- Fractional knapsack problem: 탐욕 알고리즘으로 해결 가능하다. 0-1배낭 문제와 비슷하지만, 물건을 부분적으로 나눠서 취할 수 있다. 두 문제 모두 최적 부분 구조를 가지지만, 분할 가능 배낭 문제는 Greedy-choice Property를 가진다. 물건을 $v_i / w_i$에 따라 정렬하고, 높은 가치/무게 비율을 가지는 물건부터 배낭에 채워넣는다.


(b)는 0-1 배낭 문제다. 배낭의 크기는 50이며, 물건을 부분적으로 나눌 수 없기 때문에 배낭에 빈공간이 존재한다.
(c)는 분할 가능 배낭 문제다. 가치/무게 비율을 따지면 아이템 1 > 2 > 3 순으로 높으므로 일단 아이템 1을 배낭에 넣는다. 그 후에 2를 넣고, 남은 배낭에 3을 넣는다.
Vertex Cover 문제
정점 커버 문제는 모든 간선을 커버할 수 있는 노드들의 집합을 찾는 문제다.
문제를 해결하기 위해서는, 일단 임의의 간선을 선택해야한다.
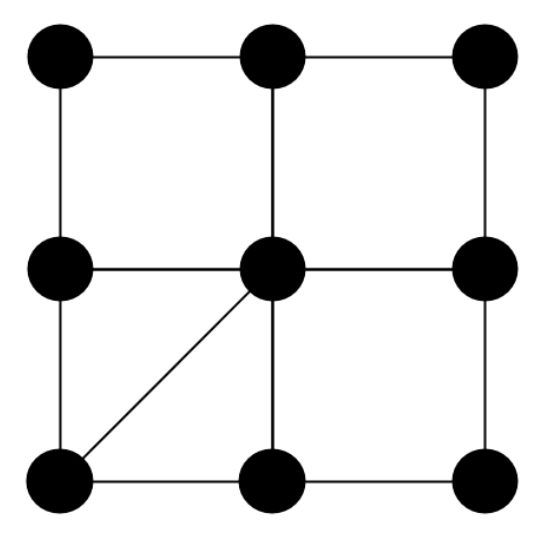
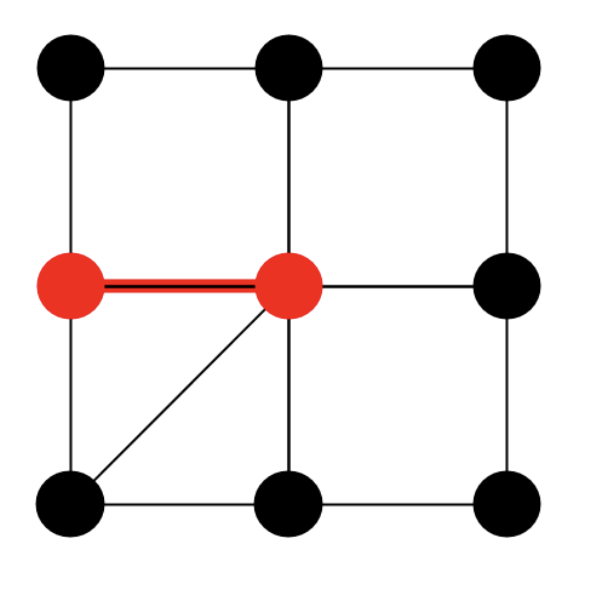
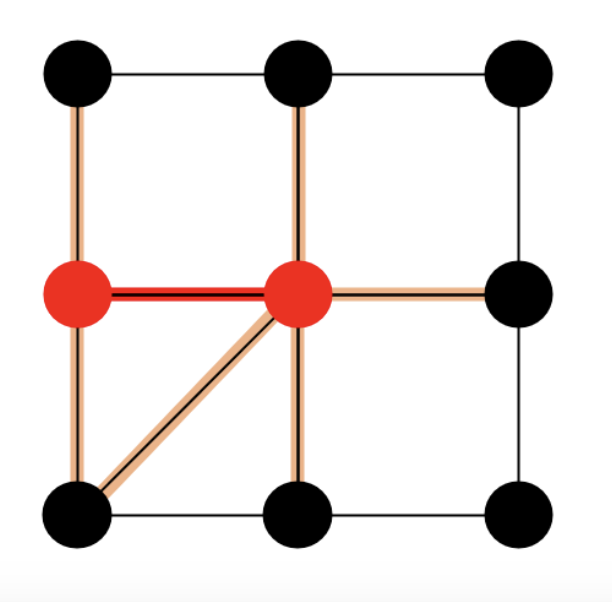
임의의 간선을 선택하면, 두 노드가 선택될 것이다. 그러면 그 두 노드에 연결된 모든 간선은 커버된 것이다. 이 과정을 모든 간선이 커버될 때까지 반복한다.
이렇게 선택된 간선의 집합을 극대매칭(maximal matching)이라고 한다.
이 문제에도 최적의 해가 존재한다. 그리고 근사해(극대 매칭의 노드 수)는 최적해(최적 노드 수)의 2배를 넘지 않는다.
근사 비율이 2인 것이다.
하지만 정점 커버 문제에 Greedy 알고리즘을 사용하면 근사 비율이 2가 넘는 경우가 존재한다.
정점 커버 문제에서는 Greedy 알고리즘을 사용하면 안된다.
** 대학교 수업을 듣고 이해한 부분을 최대한 풀어서 작성한 글입니다.
틀린 정보가 존재할 수 있으며, 언제나 피드백은 환영입니다. **
'DKU > 알고리즘 및 실습' 카테고리의 다른 글
| Binary Search Trees (0) | 2024.12.05 |
|---|---|
| Dynamic Programming (0) | 2024.12.05 |
| Hash Tables (0) | 2024.12.04 |
| Single-Source Shortest Paths (0) | 2024.12.03 |
| Minimum Spanning Trees (0) | 2024.11.20 |
