Manufacturing Problem
공장에서 생산 공정을 최적화하기 위한 문제다.
공장의 생산 라인 사이에서 가장 빠른 경로를 찾아, 제품이 공정을 완료하는데 걸리는 시간을 최소화시키는 것이다.

사진에는 두 개의 부품 조립 라인이 있고, n개의 스테이션을 가지고 있다.
라인 i에 있는 j번째 스테이션은 $S_{i, j}$로 표기되고, 이 스테이션에서의 조립 시간을 $a_{i, j}$로 표기한다.
이제 하나의 부품이 공장에 들어와 라인 i에 도착하며, $e_i$의 시간을 갖는다.
부품이 j번째 스테이션을 통과하고, 다른 라인의 j+1 번째 스테이션으로 향한다. 같은 라인에서의 스테이션을 이동할 때는 비용이 따로 들지 않지만, 다른 라인으로 향할 때는 $t_{i, j}$만큼의 시간이 든다.
n번째 스테이션에서 나온 후, 완성된 부품이 공장을 나가기까지 $x_i$만큼의 시간이 든다.
공장을 최적화하기 위해서는 라인 1과 라인2에서 최소한의 시간이 드는 스테이션만을 선택해야 한다.

이제 각각의 시간이 표시된 그림이다. 진하게 색칠된 경로가 최적화된 공장 루트이다.
그림 (b)처럼 테이블을 작성하여 문제를 해결할 수 있다.
$f_1[j]$은 라인 1을, $f_2[j]$는 라인2를 나타내며, j는 스테이션을 나타낸다.
먼저 $f_1[1]$을 작성해보자. 라인 1로 입장할 때는 2의 시간이 걸리며, 스테이션 $S_{1,1}$에서는 7의 시간이 걸리므로 총 9의 시간이 걸린다.
$f_2[1]$도 계산해보면, 라인 2로 입장할 때는 4의 시간이, 스테이션 $S_{2, 1}$에서는 8의 시간이 걸리므로 총 12의 시간이 걸린다.
$f_1[2]$는 $S_{1,1}$에서 받았을 때와, $S_{2,1}$에서 받았을 때를 비교하여 더 작은 값을 적는다. $S_{1,1}$에서 받는 시간(9 + 9)이 더 작으므로 18을 기입하는데, 이때 $l_1[2]$에도 1을 작성한다. 1라인에서 부품을 받았다는 뜻이다.
$f_2[2]$도 $S_{1,1}$에서 받았을 때와, $S_{2,1}$에서 받았을 때를 비교하여 더 작은 값을 적는다. $S_{1,1}$에서 받는 시간(9 + 2+ 5)이 더 작으므로 16을 기입하는데, 이때 $l_2[2]$에도 1을 작성한다. 1라인에서 부품을 받았다는 뜻이다.
이러한 과정을 반복하면 f테이블과 l테이블의 작성이 완료된다. l 테이블이 완성되면 역추적이 가능해지는데, l*(마지막으로 사용한 라인) = 1이므로 $l_1[6]$을 확인한다. 2가 적혀져 있으므로, $S_2[5]$를 사용했다는 뜻이다. $l_2[5]$를 확인하면 2가 적혀져 있으므로, $S_2[4]$를 사용했다는 뜻이다. 이처럼 역추적을 진행하여 최적의 공정을 찾을 수 있게 된다.


Matrix Multiplication: 행렬 곱셈

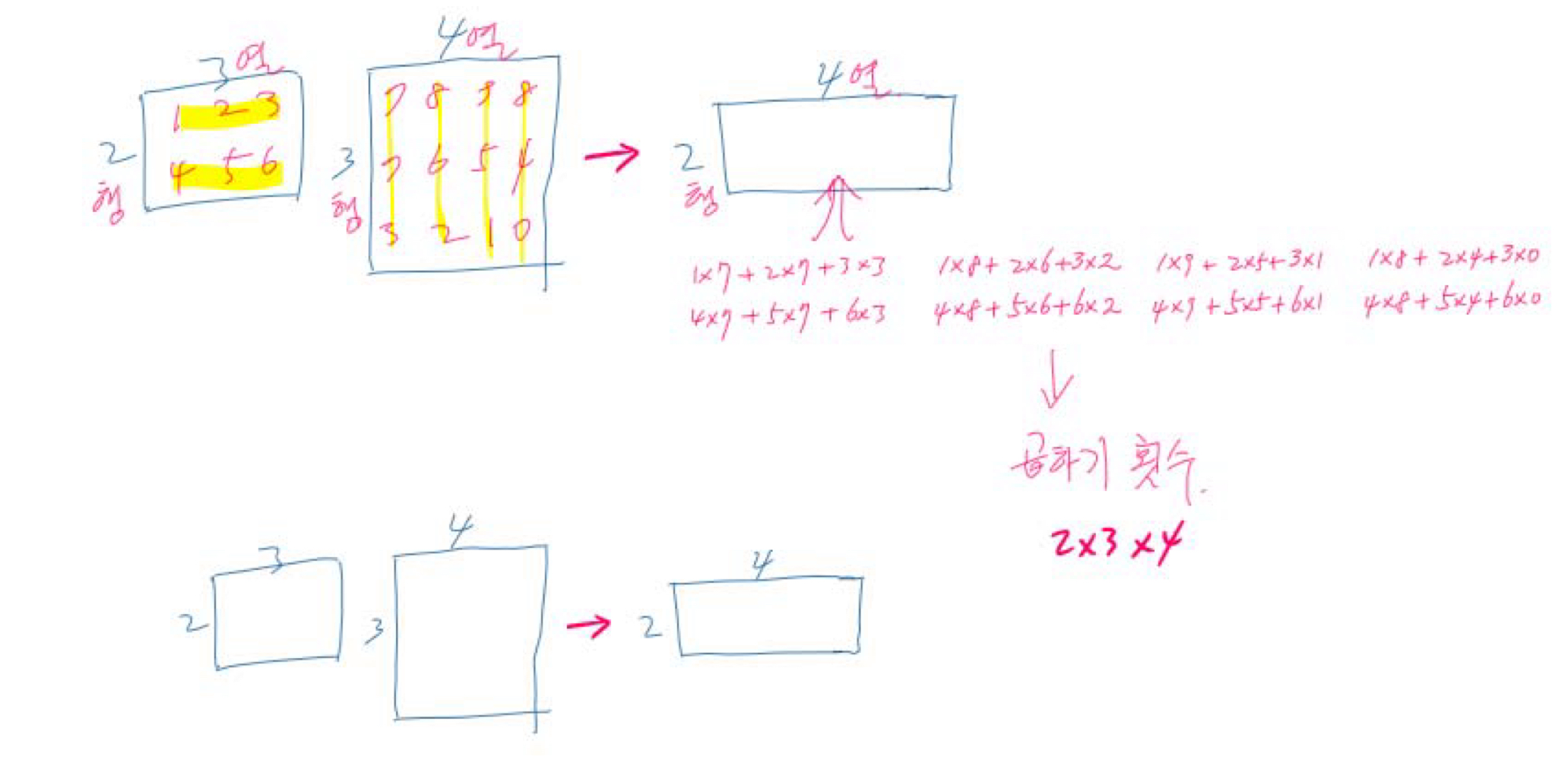
행렬의 곱셈은 어떻게 이루어지는 지 알 것이다.
2행 3열의 행렬 A와, 3행 4열의 행렬 B를 곱하면, 2행 4열의 행렬이 결과로 나오며, 2 × 3 × 4 횟수만큼의 곱하기가 실행된다.
matrix-chain multiplication problem: 행렬 곱셈 체인 문제
행렬 체인 <$A_1, A_2, ..., A_n$>이 주어지고, 각 행렬 $A_i$는 $p_{i-1}×p_i $를 가진다. (i = 1, ... , n)
목표는 행렬 곱셈 $A_1A_2 ... A_n$을 괄호로 묶어(완전 괄호화, full parenthesize) 스칼라 곱셈의 횟수를 최소화하는 것이다.
행렬 곱셈 $A_{i...k}A_{k+1...j}$를 곱할 때 필요한 스칼라 곱셈 횟수는 $p_{i-1}p_kp_j$가 된다.
- $p_{i-1}$: 왼쪽 행렬의 행 개수
- $p_k$: 두 행렬 간의 공유 차원(왼쪽 행렬의 열 개수와 오른쪽 행렬의 행 개수)
- $p_j$: 오른쪽 행렬의 열 개수

각 분할의 곱셈 횟수를 계산해보면, 다음과 같다.
$$m[i, j] = m[i, k] + m[k+1, j] + p_{i-1}p_kp_j$$
- m[i, j]: $A_i$에서 $A_j$까지의 최적 괄호화 비용
- m[i, k]: $A_i$에서 $A_k$까지의 최적 괄호화 비용
- m[k+1, j]: $A_{k+1}$에서 $A_j$까지의 최적 괄호화 비용
- $p_{i-1}p_kp_j$: 이루어지는 총 곱하기 횟수(비용)
위 사진을 설명해보자면, m[1, k] + m[k+1, 6] + $p_0p_kp_6$이 나온다.
$A_4A_5A_6$ = m[4, 6]을 계산해자면, $(A_4A_5)A_6$ 또는 $A_4(A_5A_6)$으로 계산할 수 있다.
$(A_4A_5)A_6$: m[4, 5] + m[6, 6] + $p_3p_5p_6$
$A_4(A_5A_6)$: m[4, 4] + m[5, 6] + $p_3p_4p_6$
이 중 더 작은 값을 선택하면 되는 것이다.

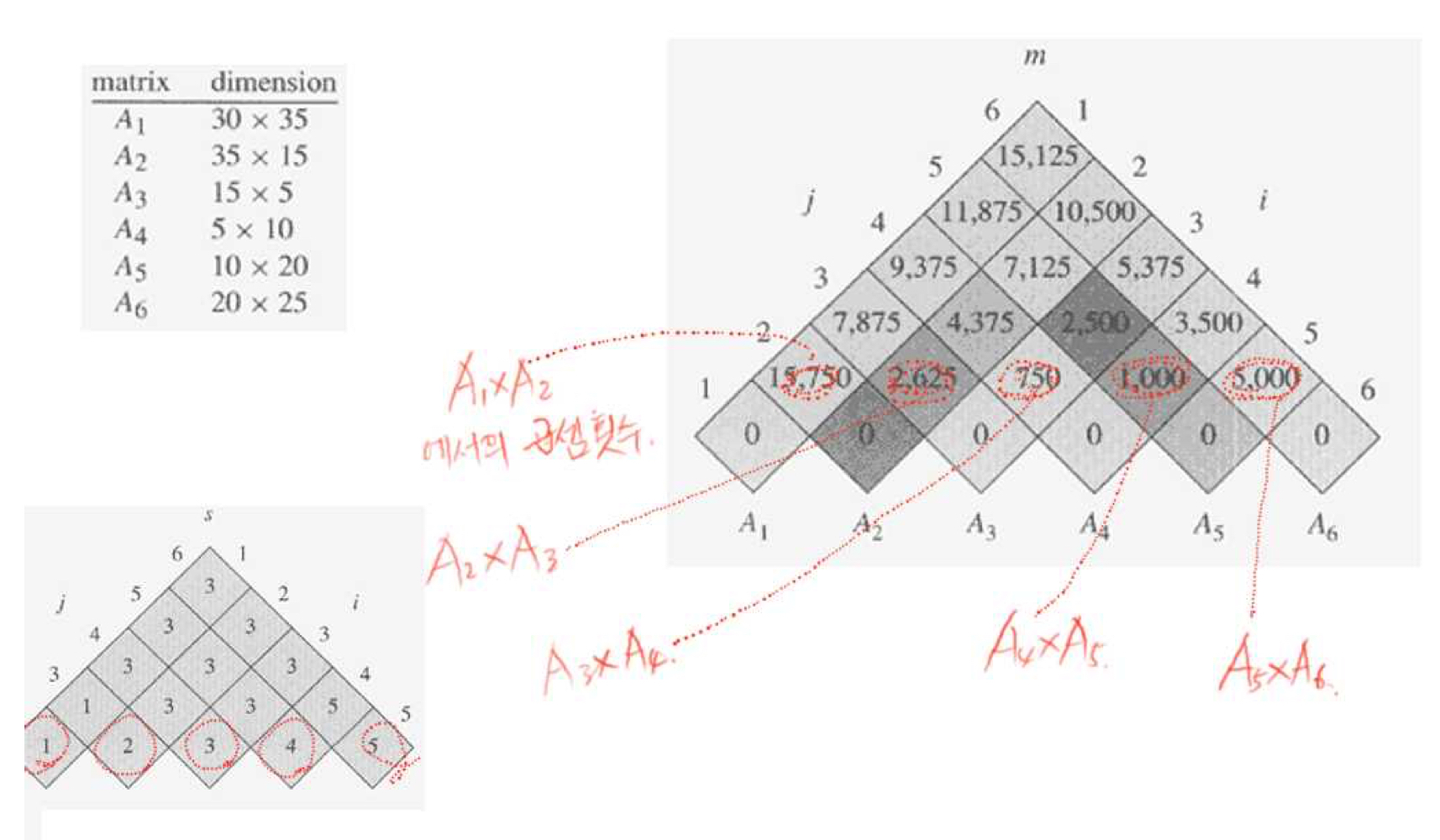
예시를 보자.
m[i, i] = 0이므로 맨 밑에 줄은 모두 0이 된다.
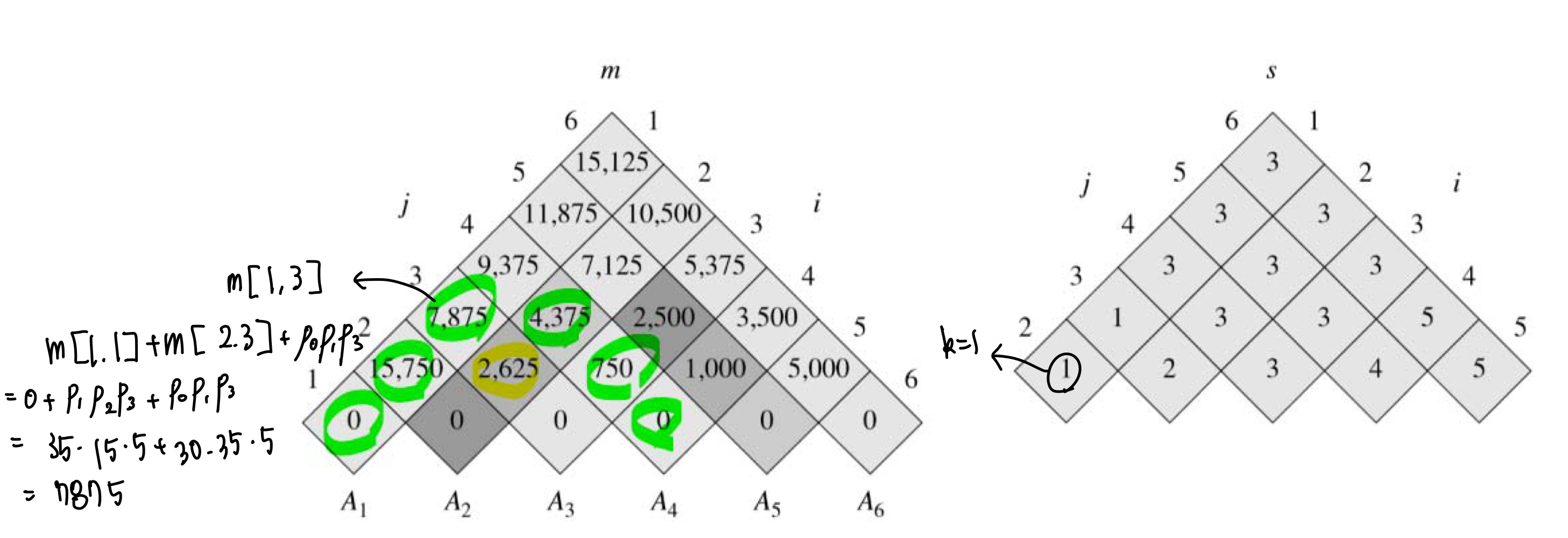
m[1, 3]의 최소 값은 Matrix-Chain-Order를 통해 s[1, 3] = 1로 구하면 된다고 알아냈다.
그러면 $A_1(A_2A_3)$이 최소값이고, 계산하면 7,875가 나오는 것이다.
** 대학교 수업을 듣고 이해한 부분을 최대한 풀어서 작성한 글입니다.
틀린 정보가 존재할 수 있으며, 언제나 피드백은 환영입니다. **
'DKU > 알고리즘 및 실습' 카테고리의 다른 글
| Red-Black Trees (3) | 2024.12.06 |
|---|---|
| Binary Search Trees (0) | 2024.12.05 |
| Greedy Algorithms (0) | 2024.12.04 |
| Hash Tables (0) | 2024.12.04 |
| Single-Source Shortest Paths (0) | 2024.12.03 |
