레드-블랙 트리는 이진 탐색 트리에 1비트 속성을 추가한 구조로, 각 노드는 빨강 또는 검정색으로 색칠된다.
모든 리프 노드는 NIL이며, 검정색으로 칠해져 있다.
이를 레드-블랙 트리 T의 모든 리프에 대해 single sentinel 노드 nil[T] 라고 한다.
color[nil[T]]는 항상 검은색이며, 루트 노드의 부모도 nil[T]다.
레드-블랙 트리는 이진 탐색 트리의 모든 속성을 상속받고, nil[T]에 저장된 키 값은 중요하지 않으므로 무시한다.
Properties of red-black trees
레드-블랙 트리는 트리의 균형을 유지하기 위해 다음 다섯 가지 속성을 만족한다.
- 모든 노드는 빨강 또는 검정이다.
- 트리의 루트 노드는 항상 검정색이다.
- 모든 리프 노드(센티널 nil[T])는 항상 검정색이다.
- 빨강 노드의 자식은 항상 검정색이여야한다. 즉, 루트에서 리프까지의 단순 경로에는 빨강 노드가 연속으로 두 번 나타날 수 없다.
- 모든 노드에 대해, 해당 노드에서 하위 리프 노드로 가는 모든 경로에는 같은 개수의 검정 노드가 포함된다. 이 값을 black height 라고 부른다.

Height of red-black trees
노드의 높이는 노드에서 리프까지의 가장 긴 경로에 포함된 간선의 개수를 의미한다.
노드 x의 Black-height은 (bh(x))로 표현되며, x에서 리프까지의 경로에 포함된 검정 노드의 수를 의미한다. 여기서 x 자신은 포함하지 않는다. 속성 5에 의해 검정 높이는 잘 정의된다.
Claim. 임의의 높이 h를 가진 노드의 검정 높이는 $b \geq h/2$를 가진다.
Proof. 속성 4에 따르면, 리프까지의 경로에 포함된 빨강 노드의 수는 최대 h/2 이다. 따라서 검정 노드는 최소 h/2 이상이 된다.
Claim. 임의의 노드 x를 루트로 하는 서브트리는 최소 $2^{bh(x)}-1$개의 내부 노드를 포함한다.
Proof. x의 높이에 대한 수학적 귀납법을 사용한다.
- Basis: x의 높이가 0일 때, x는 리프 노드이며 bx(h) = 0 이다. 이 경우, x를 루트로 하는 서브트리는 내부 노드가 없으므로 $2^0 - 1 =0$을 만족한다.
- Inductive step: 귀납을 위해, x의 높이가 h이고, bh(x) = b라고 가정한다. x의 자식 노드 각각의 높이는 h-1이며, 해당 자식 노드의 검정 높이는 다음 중 하나다. 자식이 빨강 노드인 경우 b이며, 자식이 검정 노드인 경우 b-1이다. 귀납 가정에 의해, 각 자식은 $2^{bh(x)-1}-1$개의 내부 노드를 포함한다.
- x를 루트로 하는 서브트리는 $2×(2^{bh(x)-1}-1)+1 = 2^{bh(x)}-1$을 만족한다. 여기서 +1은 x 자체를 포함한 것이다.
Lemma. 내부 노드 n개가 있는 레드-블랙 트리의 높이는 $2\lg (n+1)$ 이하다.
Proof. 위의 두 가지 주장, $b \geq h/2$와 서브트리 내부 노드 수 $\geq 2^b -1$ 를 사용한다.
내부 노드 수가 n이니, $n \ geq 2^b -1$
양변에 1을 더하면, $n+1 \geq 2^b$
로그를 취하면, $\lg (n+1) \ geq b$
$b \geq h/2$ 이므로, $h \leq 2b$이다. 따라서, $h \leq 2\lg (n+1)$가 된다.

레드-블랙 트리의 모든 노드는 검정색 아니면 빨강색인 것을 볼 수 있으며, 빨강 노드의 자식들은 모두 검정이다.
또한 각 노드에서 하위 리프 노드로 가는 모든 경로에는 같은 수의 검정 노드가 포함된다.
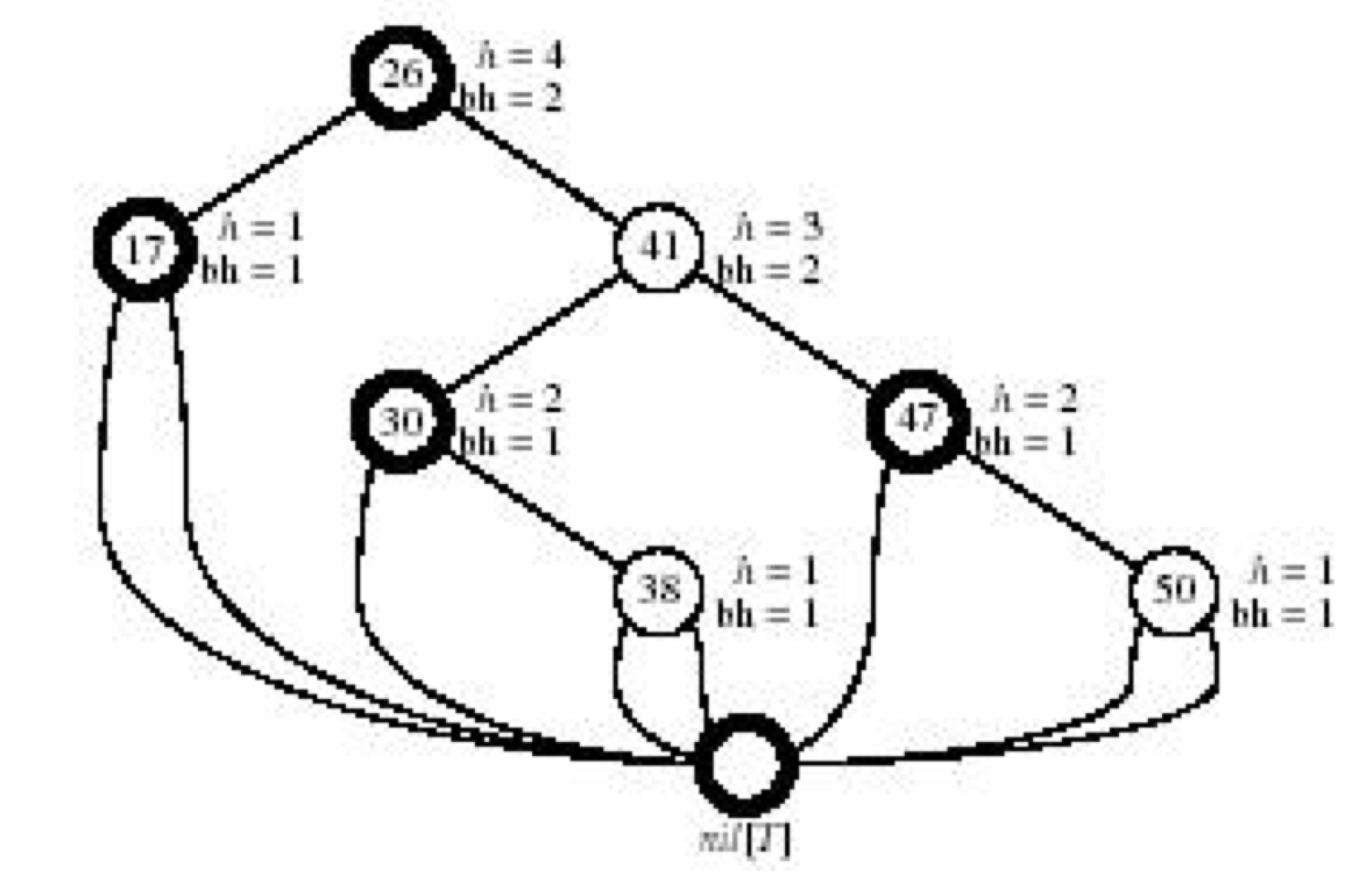
(a) nil로 보이는 모든 리프노드는 검정색이다. nil이 아닌 모든 노드는 각각 black-height이 표시되어 있다.
(b) 같은 레드-블랙 트리지만, 각 NIL이 하나의 센티널 nil[T]로 대체 되었다. 센티널 노드는 항상 검정색이며, black-height은 생략되었다. 루트 노드의 부모 역시 센티널 노드이다.
(c) 같은 레드-블랙 트리지만, 각 리프노드와 루트 노드의 부모 노드까지 생략되었다. 주로 이렇게 생략된 그림을 사용한다.
Operations on red-black trees
Minimum, Maximum, Successor, Predecessor, Search 모두 이진 탐색 트리(BST)와 마찬가지로 O(height)시간에 수행된다.
따라서 레드-블랙 트리에서는 높이가 $O(\log n)$으로 제한되므로, 해당 연산의 시간 복잡도는 $O(\log n)$이다.
하지만 삽입과 삭제는 단순하지 않다. (이번 수업에서 삭제는 다루지 않는다.
각 연산이 레드-블랙 트리의 속성을 유지하도록 추가적인 처리가 필요하다.
삽입 시에는, 새로 삽입된 노드의 색상을 결정해야한다.
빨강으로 설정한다면, 속성 4를 위반할 수 있고, 검정으로 설정한다면, 속성 5를 위반할 수도 있다.
삭제 시에는, 삭제된 노드의 색상에 따라 문제가 달라진다.
빨강 노드를 삭제하는 경우에는 문제가 발생하지 않는다. 검정 높이에는 변화가 없으며, 두 개의 빨강 노드가 연속으로 등장하지 않게되기 때문이다. 속성 2도 위반되지 않는다. 삭제된 노드가 빨강이라면 루트 노드일 수가 없기 때문이다.
문제는 검정 노드를 삭제하는 경우다. 두 개의 빨강 노드가 연속적으로 나타날 수 있으며, 검정 높이에 변화가 생길 수 있다. 또한 삭제된 노드가 루트였다면, 새 루트가 빨강색이 될 가능성도 있다.
Rotations
기본 트리 구조를 재조정하는 연산이다. 레드-블랙 트리를 균형 잡힌 이진 탐색 트리로 유지하기 위해 필요하다.
로컬 포인터 구조를 변경하여 트리를 재조정하며, 이때 이진 탐색 트리의 속성은 유지된다. 연산은 포인터 변경만 포함하므로 시간 복잡도는 O(1)이다.
왼쪽 회전과 오른쪽 회전이 있으며, 두 회전은 서로 역(inverse)관계에 있다.
레드-블랙 트리와 트리 내의 특정 노드에서 적용되며, 회전을 통해 트리의 지역적 불균형을 조정하여 레드-블랙 트리 속성을 복원한다.

Left-Rotate(T, x)는 상수개의 포인터를 바꿈으로써 두 노드를 왼쪽에서 오른쪽처럼 만든다.
$\alpha, \beta, \gamma$는 임의의 서브트리를 나타낸 것이다. 여기서 이진 탐색 트리의 속성은 보존된다.
Left-Rotate의 동작은 특정 노드 x를 기준으로 오른쪽 자식 y를 루트로 올리고, x를 y의 왼쪽 자식으로 재배치한다.
수도 코드는 다음 가정을 기반으로 작성된다.
- right[x] = y 는 nil[T] 노드가 아니여야한다.
- 루트의 부모는 항상 nil[T]이다.
Right-Rotate는 Left-Rotate의 대칭 연산이다. left와 right를 모든 곳에서 교환하면 Right-Rotate의 수도코드가 생성된다.

로테이션 전:
x의 왼쪽 서브트리(9) $\leq$ x의 key값(11) $\leq$ y의 왼쪽 서브트리(14) $\leq$ y의 key값(18) $\leq$ y의 오른쪽 서브트리(19)
로테이션은 y의 왼쪽 서브트리를 x의 오른쪽 서브트리로 바꾼다.
로테이션 후:
x의 왼쪽 서브트리(9) $\leq$ x의 key값(11) $\leq$ x의 오른쪽 서브트리(14) $\leq$ y의 key값(18) $\leq$ y의 오른쪽 서브트리(19)
Insertion
RB-Insert 연산은 일반적인 BST의 삽입과 동일하게 시작하지만, 삽입 후 레드-블랙 트리의 속성을 복원하기 위해 추가 작업을 수행한다.
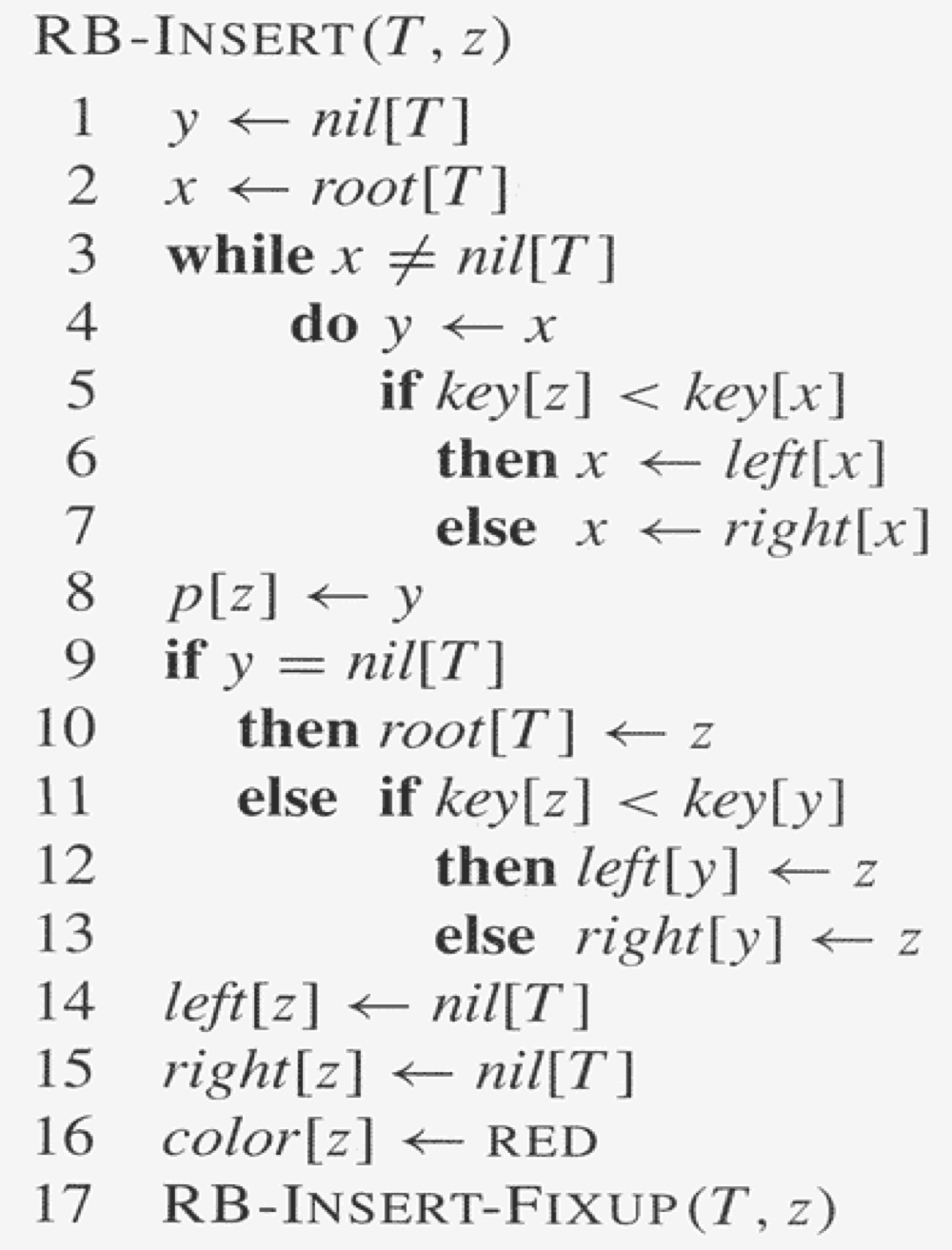
새로운 노드 z를 트리에 삽입하고, 삽입된 노드 z는 기본적으로 빨강으로 색칠된다.
삽입으로 인해 레드-블랙 트리의 특정 속성이 위반될 수 있다. 어떤 속성이 위반될 가능성이 있는지 점검한다.
- 속성 1: 위반될 가능성 없음
- 속성 2: 만약 z가 루트라면, 위반된다.
- 속성 3: 위반될 가능성 없음
- 속성 4: z의 부모 p[z]가 빨강이라면, 위반된다.
- 속성 5: 삽입 자체로는 위반되지 않는다.
위반된 속성을 제거하기 위해서 RB-Insert-Fixup이 호출된다.
주로 속성 2와 4를 복구하며, 트리 구조를 수정하고 색상을 조정하여 레드-블랙 트리의 균형을 복원한다.

Loop Invariant:
while 루프의 각 반복 시작 시점에 다음 조건이 유지된다.
- 노드 z는 빨강이다.
- 최대 하나의 레드-블랙 속성이 위반된다.
Initializaiton: 삽입 후, z는 빨강이며 부모 p[z]와의 관계로 인해 위반이 있을 수 있다. 따라서 루프가 시작될 때 불변식이 성립한다.
Termination: 루프는 p[z]가 검정일 때 종료한다. 이 경우, 속성4는 더 이상 위반되지 않는다. 속성 2가 위반될 가능성이 있지만, 루프의 마지막 줄에서 이를 수정한다. (루트를 검정으로 변경)
Maintenance: z가 루트라면 루프에서 빠져나온다. 이때 p[z]는 센티널 nil[T]이고, 이는 항상 검정이다. 루프가 진행될 때 유일하게 속성 4가 위반된다.
z의 상태와 p[z], y(p[z]의 형제)를 기반으로 트리의 균형과 색상을 수정한다.
총 6가지 케이스가 있는데, 3가지는 p[z]가 왼쪽 자식일 때고, 나머지 3가지는 대칭적 상황으로 p[z]가 오른쪽 자식일 때다.
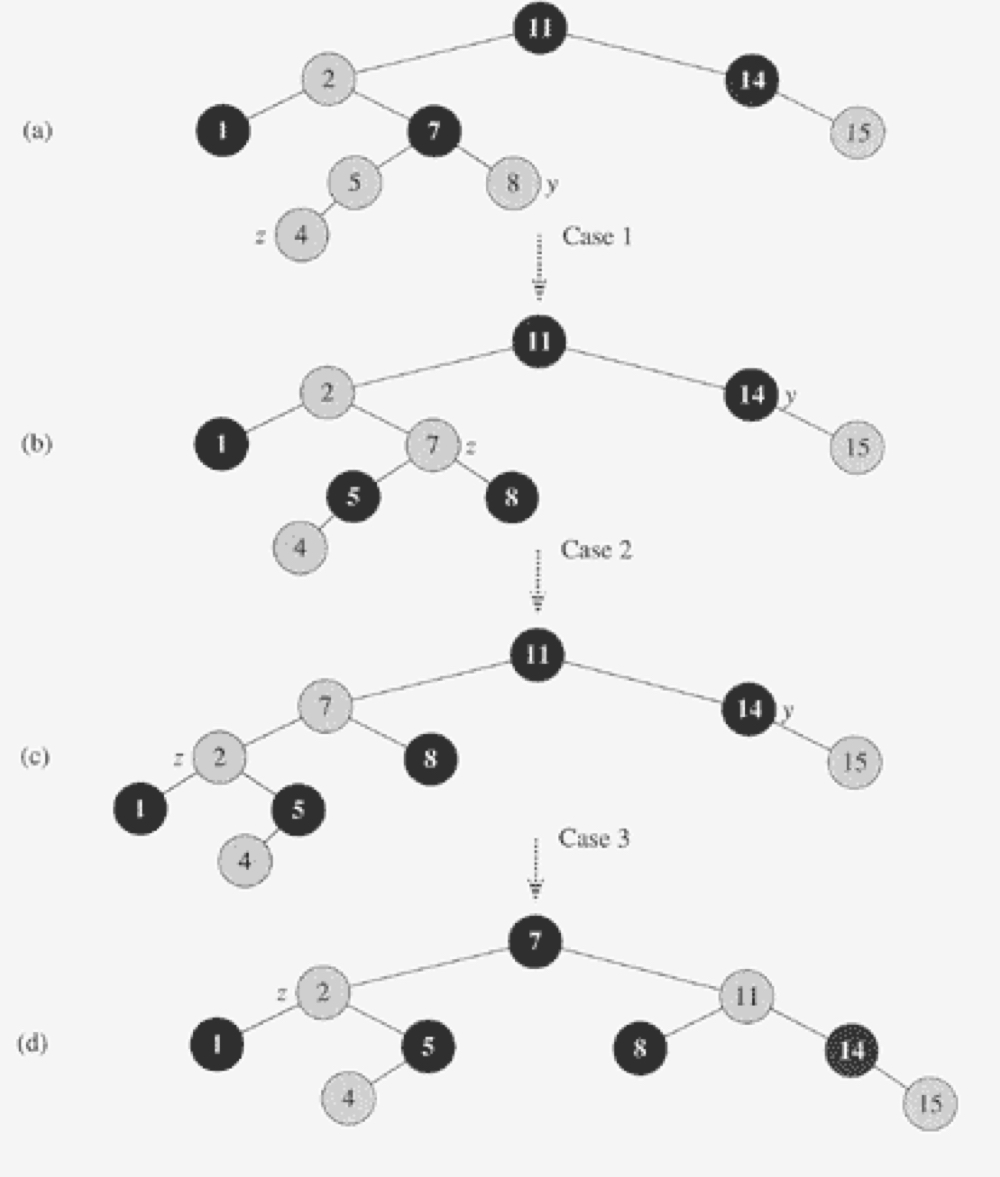
Case 1: y가 빨강인 경우
p[p[z]](z의 조부모)는 검정이여야 한다. z와 p[z]가 모두 빨강이고, 속성 4 외의 다른 위반은 존재하지 않기 때문이다.
- p[z]와 y를 검정으로 만든다: 이로 인해 이제 z와 p[z]가 둘 다 빨강인 상태는 해소된다. 하지만 속성 5가 위반될 가능성이 있다.
- p[p[z]]를 빨강으로 만든다: 이를 통해 속성 5를 복원한다.
- 다음 반복에서는 p[p[z]]를 새로운 z로 설정한다.
Case2: y가 검정이고, z가 오른쪽 자식인 경우
- p[z]를 기준으로 왼쪽으로 회전한다: 이제 z는 왼쪽 자식이 되며, z와 p[z] 모두 빨강이 된다.
바로 Case3으로 전환된다.
Case3: y가 검정이고, z가 왼쪽 자식인 경우
- p[z]를 검정으로 만들고, p[z[z]]를 빨강으로 만든다.
- 그런 다음 p[z[z]]를 기준으로 오른쪽으로 회전한다: 이제 연속된 빨강 노드가 없어진다.
- p[z]는 검정이 된다: 이로 인해 반복이 더 이상 필요하지 않다.
RB-Insert에서 RB-Insert-Fixup 호출까지는 $O(\log n)$시간이 소요된다.
RB-Insert-Fixup 내에서, 각 반복은 O(1)시간 안에 수행된다. 각 반복은 마지막 반복이거나, z를 트리에서 2레벨 위로 이동시킨다.
트리의 높이가 $O(\log n)$이므로, 최대 $O(\log n)$번 반복된다. 또한, 전체 과정에서 최대 2번의 회전만 발생한다.
결국, 레드-블랙 트리의 삽입 연산은 $O(\log n)$ 시간이 소요된다.
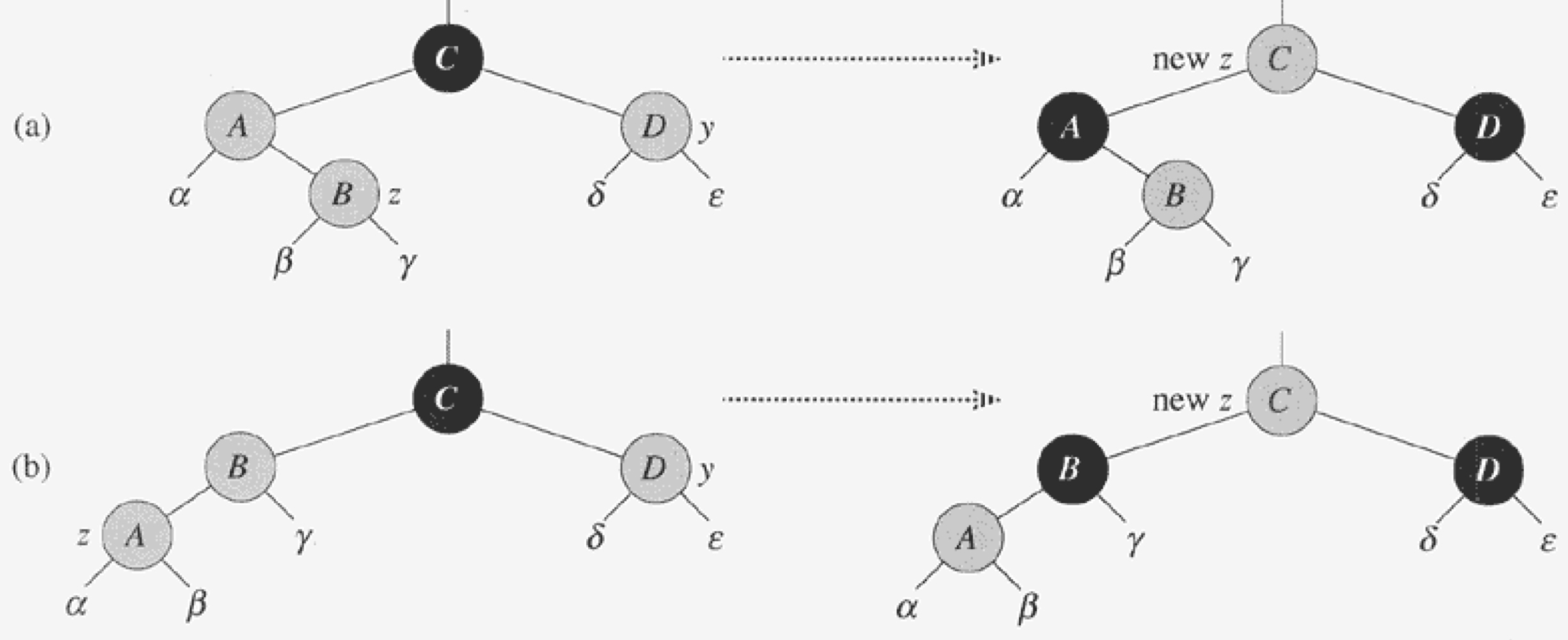
z와 p[z] 둘 다 빨강이므로, 속성 4가 위반되었다.
(a) z가 오른쪽 자식일 때와 (b) z가 왼쪽 자식일 때의 두 경우 모두 같은 과정을 따른다.
각 $\alpha, \beta, \gamma, \delta, \epslion$ 모두 블랙 루트를 가지며, 같은 black-height을 가지고 있다.
case 1을 위한 코드는 몇 개의 노드 색깔을 바꾸면서 속성 5를 보존한다.
while 루프는 p[z[z]]를 새로운 z로 선정하면서 루프를 반복한다.
이제 속성 4에 대한 위반은 새로운 z에 대해서만 발생할 수 있다. (새로운 z가 빨강이고, 그 부모 역시 빨강이라면)
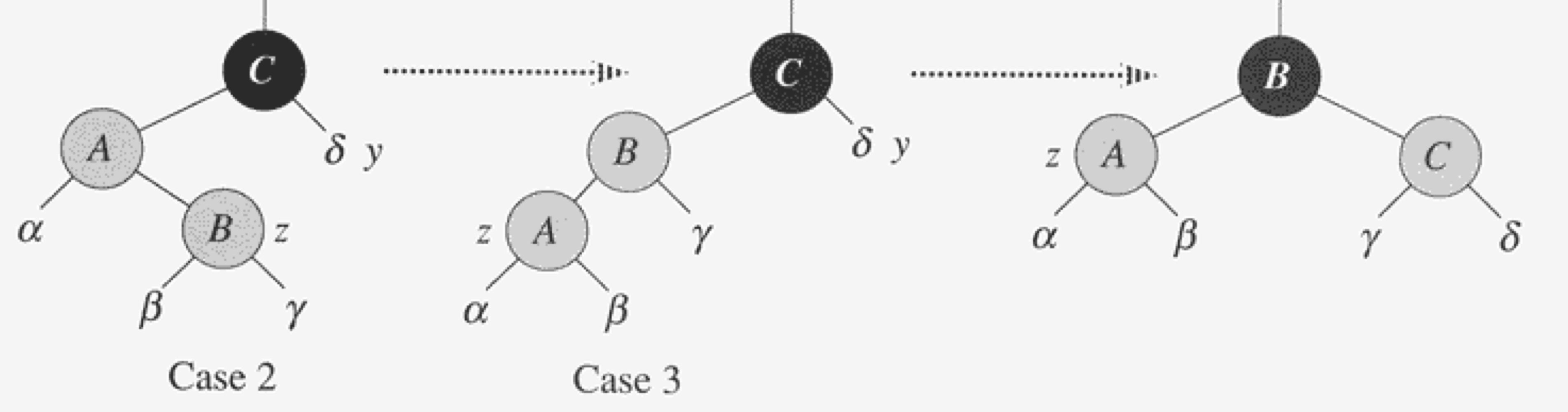
Case 2와 Case 3 어느 경우에던 간에, 속성 4는 항상 위반된다. z와 p[z]가 모두 빨강이기 때문이다.
Case 2는 왼쪽 로테이션으로 인해 Case 3로 전환되고, Case 3는 노드 색상 바꾸기와 오른쪽 로테이션을 발생시킨다.
이후에 while루프는 속성 4가 복원되었기 때문에 종료된다.
Approximation Algorithm: 근접 알고리즘
근접 알고리즘은 NP-hard 문제를 대상으로 최적해가 아닌 근접해를 구하는 알고리즘이다.
주로 기존 알고리즘들을 종합적으로 활용하며, 최적해에 대한 근접 비율(approximation ratio)을 제시한다.
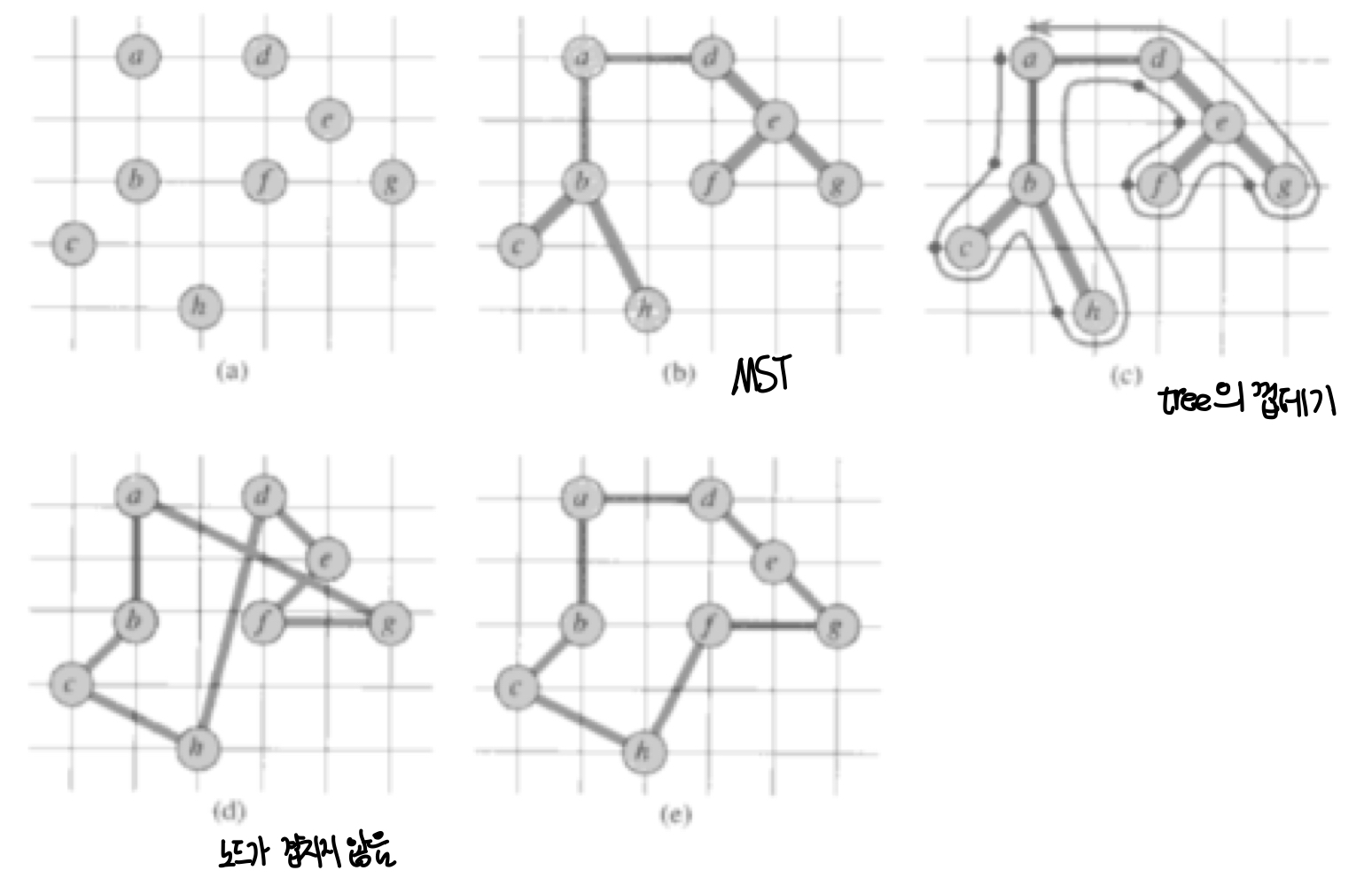
대표적인 예시로 TSP가 있다.
그래프가 주어지면, 하나의 노드에서 출발하여 모든 노드를 거쳐 출발 노드로 돌아오는 경로를 찾는 문제다.
** 대학교 수업을 듣고 이해한 부분을 최대한 풀어서 작성한 글입니다.
틀린 정보가 존재할 수 있으며, 언제나 피드백은 환영입니다. **
'DKU > 알고리즘 및 실습' 카테고리의 다른 글
| Amortized Analysis (0) | 2024.12.06 |
|---|---|
| Binary Search Trees (0) | 2024.12.05 |
| Dynamic Programming (0) | 2024.12.05 |
| Greedy Algorithms (0) | 2024.12.04 |
| Hash Tables (0) | 2024.12.04 |