탐색 트리란, 동적 집합 연산을 지원하는 자료구조이다. 딕셔너리와 우선순위 큐로 사용 가능하다.
기본 연산은 트리의 높이에 비례하는 시간이 소요된다.
- 노드가 n개인 완전 이진 트리인 경우: $O(\log n)$
- 노드가 n개인 선형 체인의 경우: $O(n)$
탐색 트리의 유형에는 이진 탐색 트리, 레드-블랙 트리, B-트리 등이 있다
Binary Search Trees
트리 높이를 h라 할 때, 많은 동적 집합 연산을 $O(h)$시간 안에 수행할 수 있다.
이진 트리는 각 노드가 객체로 구성된 linked list 자료 구조로 표현된다.
root[T]는 트리 T의 루트를 가리키며, 각 노드는 다음과 같은 필드를 포함한다.
- key
- left: 왼쪽 자식
- right: 오른쪽 자식
- p: 부모, p[root[T]] = NIL
저장된 key는 이진 탐색 트리 속성을 만족해야한다.
- y가 x의 왼쪽 서브트리에 있으면, $key[y]\leq key[x]$.
- y가 x의 오른쪽 서브트리에 있으면, $key[y] \geq key[x]$

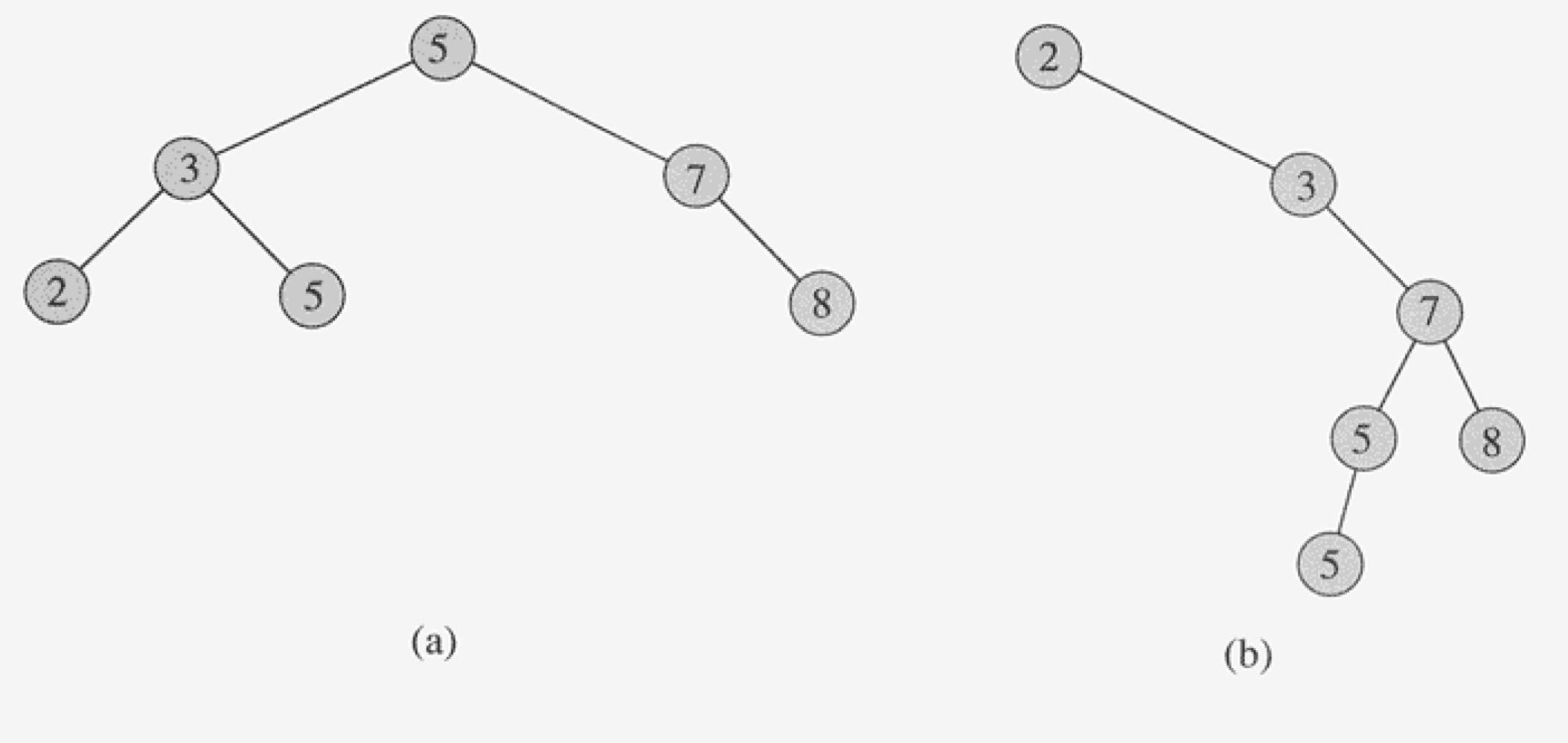
다른 이진 탐색 트리인 경우라도, 같은 집합의 값을 표현할 수 있다.
탐색 트리의 연산은 트리의 높이에 비례하게 되는데, 따라서 같은 집합을 표현한 (a), (b)여도 높이가 낮은 (a)가 실행시간이 더 짧다.
이진 탐색 트리의 속성을 이용하면 Inorder-Tree-Walk 알고리즘을 사용하여 트리에 있는 키들을 순서대로 출력할 수 있다.
트리의 요소들은 오름차순으로 출력된다.

직관적으로 중위 순회는 n개의 노드를 가진 트리에서 $O(n)$ 시간이 소요된다. 각 노드를 한번씩 방문하고 출력하기 때문이다.

Querying a binary search tree

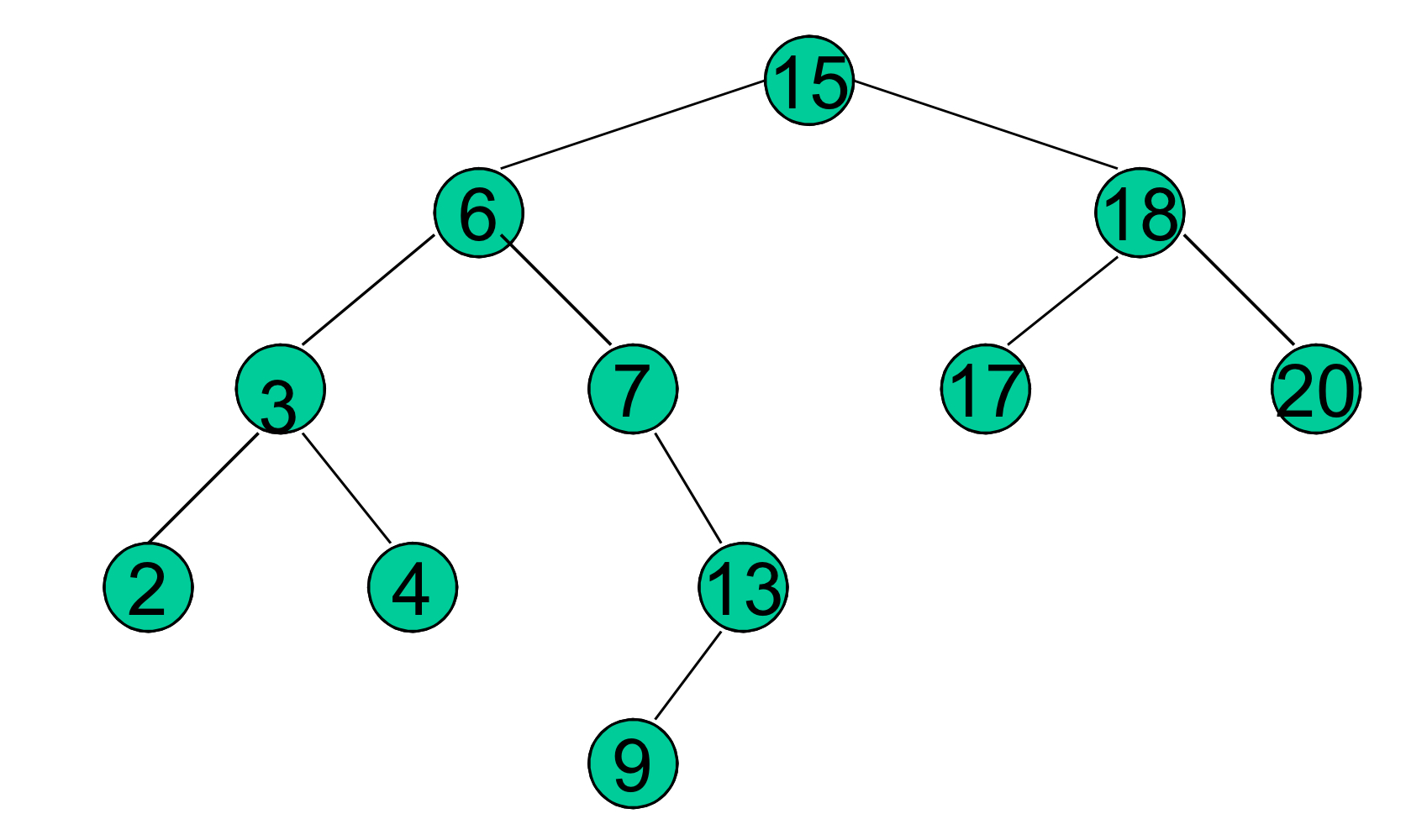
트리에서 key 13을 탐색하기 위해서는, 루트에서부터 경로 15 → 6 → 7 → 13 로 따라와야한다.
트리에서 가장 작은 key는 2며, 루트에서부터 왼쪽 포인터들만 따라오면 찾을 수 있다.
트리에서 가장 큰 key는 20이며, 루트에서부터 오른쪽 포인터들만 따라오면 찾을 수 있다.
key 15의 후임(successor)은 key 17이고, 이 17은 15의 오른쪽 서브트리 중 가장 작은 key 값을 가지고 있다.
key 13을 가진 노드는 오른쪽 서브트리를 가지고 있지 않으며, 13의 후임은 왼쪽 자식 9가 된다. 9는 가장 낮은 조상인데, 이때 9의 후임은 15가 된다.


초기 호출은 TREE-SEARCH(root[T], k) 이다. k 값을 가진 노드를 찾기 위해, 이 알고리즘은 루트에서 시작하여 아래 방향으로 경로를 따라가며 노드를 방문한다.
따라서 실행시간은 트리의 높이가 h일 때, $O(h)$가 된다.
Minimum and maximum
이진 탐색 트리의 속성에 따르면, 최소 key는 가장 왼쪽 노드에 위치하며, 최대 key는 가장 오른쪽 노드에 위치한다.
적절한 방향(왼쪽 또는 오른쪽)의 포인터를 따라가면서 NIL에 도착할 때까지 탐색하면 된다.

두 알고리즘 모두 트리의 높이 h에 비례하는 $O(h)$ 시간 복잡도를 가진다.
루트에서 시작하여 리프 노드까지 이어지는 하향 경로를 따라 노드를 방문하기 때문이다.
Successor and Predecessor
모든 노드의 key 값은 서로 다르다고 가정하자.
노드 x의 후속 노드 y는 key[y] > key[x]를 만족하는 노드 중에서 가장 작은 키를 가진 노드다. 후속 노드는 트리 구조만으로도 찾을 수 있으며, 키 값을 비교할 필요는 없다. 만약 x가 이진 탐색 트리에서 가장 큰 키를 가진 노드라면, x의 후속 노드는 NIL이다.
후속 노드를 찾는 두 가지 경우가 있다.
- x가 비어 있지 않은 오른쪽 서브트리를 가진 경우: x의 후속노드는 x의 오른쪽 서브트리에서 최솟값이다.
- x가 빈 오른쪽 서브트리를 가진 경우: 트리의 위로 이동한다. 오른쪽 자식을 따라 위로 이동하는 동안에는 항상 더 작은 키를 방문하게 된다. x의 후속 노드 y는 x가 y의 왼쪽 서브트리에서 최댓값일 때의 y이다. 즉, x가 y의 직전 노드(predecessor)일 때, y가 x의 후속 노드가 된다.

실행 시간은 트리의 높이가 h일 때, $O(h)$가 된다.
두 절차 모두 트리의 아래 방향 또는 위 방향의 노드들을 방문하기 때문이다. 따라서, 최악의 경우 트리의 높이에 비례하는 시간이 소요된다.
15의 키 값을 가진 노드의 후속 노드를 찾아보자.
오른쪽 서브트리가 비어있지 않으니, 오른쪽 서브트리에서의 최솟값을 찾는다. 그럼 17 값을 가진 노드가 탐색된다.
6의 키 값을 가진 노드의 후속 노드를 찾아보자.
오른쪽 서브트리가 비어있지 않으니, 오른족 서브트리에서 최솟값을 찾는다.그럼 7값을 가진 노드가 탐색된다.
4의 키 값을 가진 노드의 후속 노드를 찾아보자.
오른쪽 서브트리가 비어있으니, 트리의 위로 이동하여 y = 3이 된다.
y의 오른쪽 자식이 4라면, p[y]를 찾는다. 그럼 6값을 가진 노드가 탐색된다.
6의 키 값을 가진 노드의 직전 노드를 찾아보자.
왼쪽 서브트리가 비어 있지 않으니, 왼쪽 서브트리에서의 최댓값을 찾는다. 그럼 4 값을 가진 노트가 탐색된다.
Insertion and deletion
삽입과 삭제는 이진 탐색 트리로 표현된 동적 집합의 구성을 변경할 수 있도록 한다. 물론 변경 이후에도 이진 탐색 트리 속성이 유지되어야한다. 즉, 왼쪽 서브트리의 모든 키는 루트 키보다 작고, 오른쪽 서브트리의 모든 키는 루트 기보다 커야한다.
삽입은 상대적으로 삭제보다 더 단순한 연산이다. 삽입은 트리의 적절한 위치를 찾아 새 노드를 추가하는 과정이고, 삭제는 노드의 위치와 연결 구조를 변경해야 할 수 있기 때문에 더 복잡하다.

이진 탐색 트리에 값 v를 삽입하려면, 다음 과정을 따라야한다.
- 초기화: 노드 z를 생성하고, key[z] = v, left[z] = NIL, right[z] = NIL로 설정한다.
- 트리 탐색: 트리의 루트에서 시작하여 아래로 내려가면서 적절한 위치를 찾는다. x는 아래 방향으로 탐색하는 현재 노드를 가리키며, y는 x의 부모를 추적하는 포인터를 가리킨다.
- 값 비교 및 이동: 현재 노드 x의 값과 v를 비교한다. v가 x의 키보다 작으면 왼쪽 자식으로 이동하고, 크면 오른쪽 자식으로 이동한다. x가 NIL에 도달하면, z를 삽입할 올바른 위치에 도달한 것이다.
- 삽입: z의 값을 y의 값과 비교한다. v가 y의 키보다 작으면 z를 y의 왼쪽 자식으로 삽입하고, 크면 오른쪽 자식으로 삽입한다.
삽입 알고리즘은 트리의 높이가 h일 때, $O(h)$ 시간이 소요된다.

이진 탐색 트리에서 노드를 삭제하는 절차는 다음 세 가지 경우로 나뉜다.
- z가 자식 노드가 없는 경우: z를 삭제하기 위해 z의 부모 노드가 z대신 NIL을 가리키도록 만든다.
- z가 하나의 자식 노드만 가지는 경우: z를 삭제하기 위해 z의 부모 노드가 대신 z의 자식을 가리키도록 만든다.
- z가 두 개의 자식 노드를 가지는 경우: z의 후속 노드 y를 찾는다. y는 z의 오른쪽 서브트리에서 최솟값을 가지는 노드며, y는 왼쪽 자식을 가지지 않으므로 y는 1번 경우 아니면 2번 경우에 해당한다. y를 트리에서 삭제하고, z의 데이터를 y의 데이터로 교체한다.
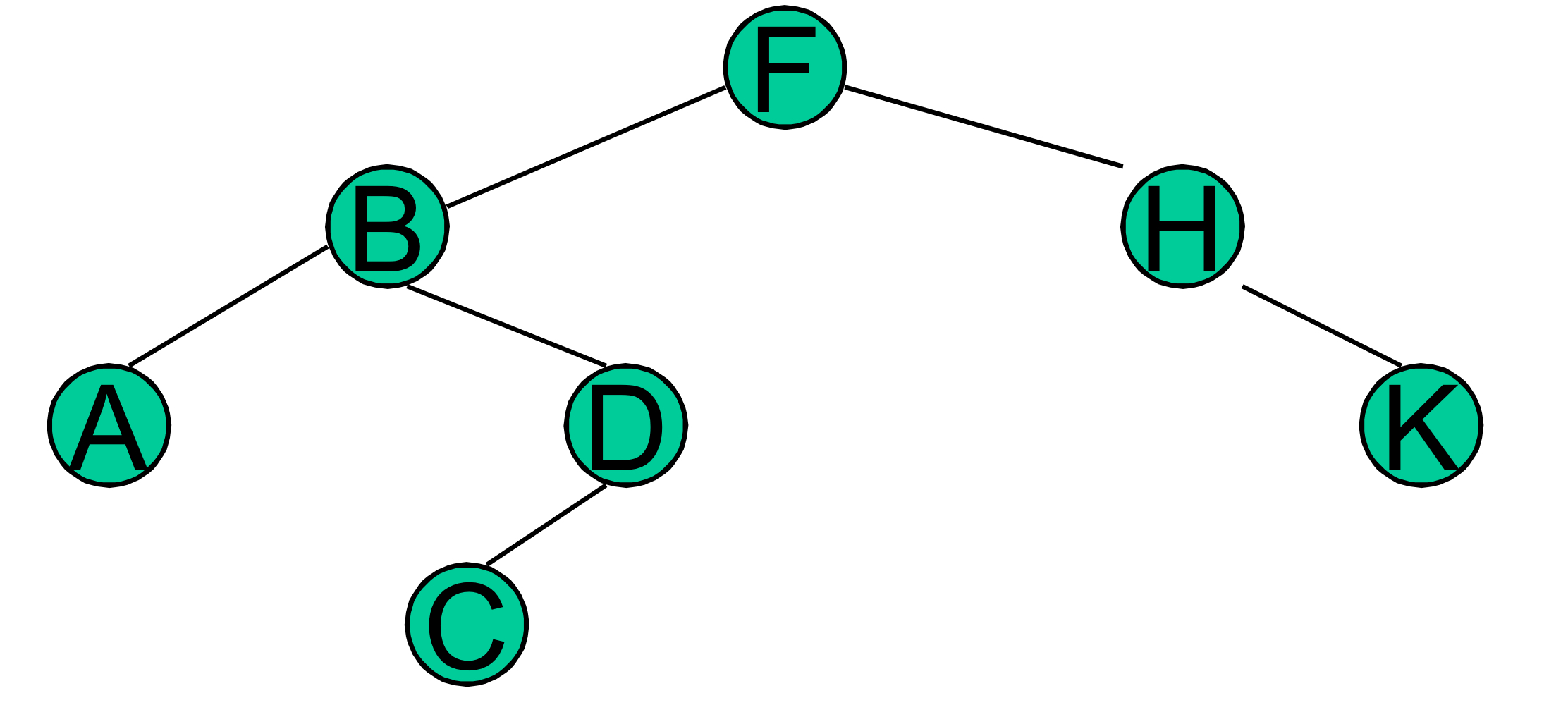
키 K를 삭제한다고 하면, K는 자식이 없으므로 H가 NIL을 가리키도록 한다.
키 H를 삭제한다고 하면, H는 하나의 자식이 있으므로 F가 K를 가리키도록 한다.
키 B를 삭제한다고 하면, 후속 노드 C를 찾은 후에 C를 삭제하고 B를 C로 대체한다.
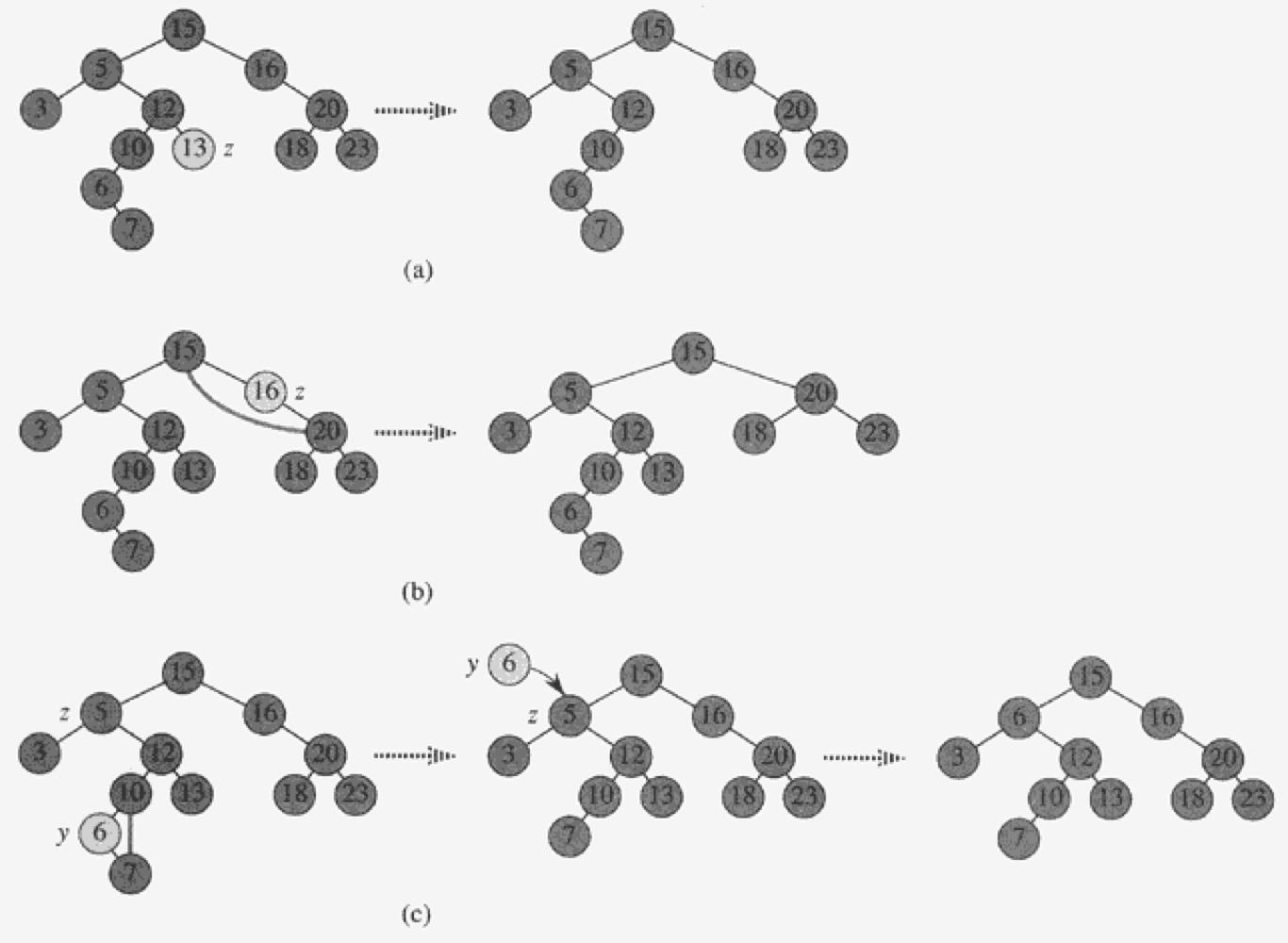
(a)에서는 z의 자식이 없으므로 12가 NIL을 가리키도록 한다.
(b)에서는 z의 자식이 하나이므로, 15가 20을 가리키도록 한다.
(c)에서는 z의 자식이 두 개이므로 일단 오른쪽 서브트리에서 최솟값을 찾는다. y를 삭제하고 z자리에 y=6을 넣어준다.
Minimizing running time
기존 분석 방식으로는, 실행 시간을 트리의 높이 h를 기준으로 분석했다.
하지만 최악의 경우, 이진 탐색 트리의 높이는 $O(n)$이 될 수 있다.
여기서 트리의 높이를 $O(\log n)$으로 보장하여 최악의 경우를 방지한다. 이를 통해 트리 연산(탐색, 삽입, 삭제)의 실행 시간을 크게 개선할 수 있다.
나중에는 이진 탐색 트리의 속성을 다양하게 변경함으로써 실행 시간을 노드 수 n을 기준으로 분석할 수 있다.
즉, 트리의 구조를 재구성 할 수 있는 것이다. 쿼리 작업은 특별한 조정 없이 수행할 수 있지만, 삽입 또는 삭제 시에는 트리 구조를 변경하는 추가 작업이 필요할 수 있다.
레드-블랙 트리는 최악의 경우 $O(n)$의 실행 시간을 가지는 일반 이진 탐색 트리의 문제를 피하기 위해 설계된 특별한 형태의 이진 트리이다. 트리의 균형을 보장하여 트리의 높이를 $O(\log n)$로 유지한다.
** 대학교 수업을 듣고 이해한 부분을 최대한 풀어서 작성한 글입니다.
틀린 정보가 존재할 수 있으며, 언제나 피드백은 환영입니다. **
'DKU > 알고리즘 및 실습' 카테고리의 다른 글
| Amortized Analysis (0) | 2024.12.06 |
|---|---|
| Red-Black Trees (3) | 2024.12.06 |
| Dynamic Programming (0) | 2024.12.05 |
| Greedy Algorithms (0) | 2024.12.04 |
| Hash Tables (0) | 2024.12.04 |