수신자가 받은 패킷이 송신자가 보낸 패킷과 다를 때, 해당 패킷에서 오류가 발생했다고 얘기한다.
이러한 오류는 잡음과 간섭에 의해 발생할 수 있다.
오류의 주요 원인들로는,
- 전자들의 무작위 운동
- 자연 현상: 번개, 태양 흑점 등
- 인간 활동: 전기 점화 시스템, 모터 및 스위칭 시스템 등
- 기호 간 간섭(Inter-symbol interference): 인접한 신호가 서로 영향을 미치는 현상
- 혼선(Crosstalk): 신호 간의 전자기적 결합에 의해 발생하는 현상
- 에코: 부적절하게 끝난 회로에서 먼 쪽으로부터 전자기 에너지가 반사되는 현상
등이 존재한다.
오류를 제어하는 방식은 두 가지로 분류된다.
- closed-loop error control scheme(폐쇄 루프 오류 제어 방식): automatic repeat request(ARQ)가 대표적인데, 수신자가 오류가 발생한 데이터를 감지한 경우 송신자에게 재전송을 요청하는 방식이다.
- open-loop error control scehme(개방 루프 오류 제어 방식): forward error correction(FEC)가 대표적인데, 송신자가 미리 오류를 보정할 수 있는 정보를 포함하여 전송하므로, 수신자가 스스로 오류를 수정할 수 있는 방식이다.
ARQ는 송신자가 수신자에게 패킷을 전송할 때, 수신자가 패킷을 수신하면 오류가 있는지 검사한다. 이 때 오류가 감지되면 수신자는 송신자에게 패킷 재전송 요청 메시지를 보낸다. 송신자가 요청 메시지를 오류 없이 수신하면 해당 패킷을 재전송해준다.
FEC는 수신자가 패킷을 수신하고 오류가 있는지 검사하는 것 까지는 ARQ와 똑같다. 다만, 오류가 감지되면 수신자는 패킷의 오류를 수정하려고 시도한다. 이 때 수신자가 오류를 수정할 수 있도록 패킷에 오류 수정에 필요한 정보가 포함되어 있어야한다.
ARQ의 종류
- Stop and Wait ARQ: 송신자는 하나의 패킷을 전송한 후, 수신자로부터 ACK을 받을 때까지 대기한다. 응답이 오지 않거나 오류가 발생하면 패킷을 재전송한다.
- Go-back-N ARQ: 송신자는 여러 패킷을 연속적으로 전송할 수 있으며, 수신자가 오류가 발생한 패킷을 감지하면 해당 패킷 이후의 모든 패킷을 재전송한다.
- Selective Repeat ARQ: 수신자는 오류가 발생한 특정 패킷만 재전송을 요청한다. 송신자는 요청된 패킷만 재전송하며, 나머지 패킷은 그래도 유지된다.
Stop and Wait ARQ
이 ARQ에서 송신자는 큐의 가장 앞에 있는 패킷을 전송한다. 송신이 준비되었고 전송할 패킷이 있는 경우 전송을 시작한다.
패킷을 전송한 후에는 ACK timer가 시작된다.
송신자는 타이머가 만료되기 전에 ACK를 수신했는지 확인한다. 만약 수신했다면, 큐의 가장 앞에 있는 패킷을 제거하고, 다음 패킷의 전송을 준비한다. 만약 아니라면, 패킷을 재전송한다.

위 예시에서 송신자는 패킷 P1을 3번, P2를 1번 전송했다.
수신자는 길이가 S(1)인 구간 동안 P1을 오류 없이 수신하고, 길이가 S(2)인 구간 동안 P2를 오류 없이 수신했다.
$T_P$는 패킷 전송 시간으로, N(bits/packet)/R(bits/second)로 계산할 수 있다.
$T_{PRO}$는 송신자와 수신자 간의 전파 지연 시간으로, d(거리)/v(속도)로 계산할 수 있다.
Time-out Period
타임 아웃 기간은 송신자가 패킷 전송을 마친 후에 시작되는 시간 간격이다. 이 기간 동안 송신자는 수신자로부터 오류 없는 패킷 수신에 대한 긍정적 확인 응답(ACK)을 기다린다.
타임 아웃 기간이 너무 긴 경우, 수신자가 오류가 있는 패킷을 수신 했을 때, 불필요한 시간 낭비를 하게 된다.
타임 아웃 기간이 너무 짧은 경우, 수신자가 오류 없는 패킷을 수신했음에도 송신자는 불필요하게 패킷은 재전송하게 된다.
따라서 최적의 타임 아웃 시간은, $T^{*}_{TO} = 2T_{PRO} + T_{ACK}$ 이다.



Performance
먼저 Stop and Wait ARQ의 성능을 분석하기 위해 사용되는 매개변수에 대해서 알아보자.
- $R$: 데이터 전송 속도
- $N_{PL}$: 페이로드의 길이, 페이로드란 전송되는 데이터의 유용한 부분이다.
- $N_H$: 헤더의 길이, 헤더란 데이터와 함께 전송되는 제어 정보이다.
- $N_{ACK}$: ACK 메시지의 길이
- $v$: 전파 속도
- $d$: 송신자와 수신자 간의 물리적 거리
- $p_{B}$: 전송 중에 비트의 오류가 발생할 확률, 이는 채널의 품질을 나타내며 0에서 1사이의 값을 가진다.
다음은 성능 분석에서 사용되는 유도된 파라미터이다.
- $N_P$: 패킷의 길이다. $N_H + N_{PL}$
- $T_P$: 패킷 전송 시간이다. $(N_H + N_{PL})/R$
- $T_{ACK}$: 긍정적 ACK의 전송 시간이다. $N_{ACK}/R$
- $T_{PRO}$: 전파 지연이다. $d/v$
- $p_P$: 패킷 오류 발생 확률이다. $1 - (1 - p_B)^{N_H + N_{PL}}$
다음은 성능 분석을 위한 환경 조건이다.
- 송신자 포화 상태: 송신자가 항상 전송할 패킷을 보유하고 있다. 즉, 송신자는 전송할 패킷이 없어서 대기 상태가 되는 일이 없다.
- 패킷 오류 발생 확률($p_P$): 송신자가 전송한 각 패킷에서 독립적으로 오류가 발생할 확률은 $p_P$이다. 각 패킷의 오류는 서로 독립적이며 동일한 확률로 발생한다는것이다.
- 수신자의 패킷 오류 검출: 수신자는 수신한 패킷에 오류가 있는 경우 이를 완벽하게 감지할 수 있다.
- ACK 오류 없음: 모든 ACK에서는 오류가 발생하지 않고 송신자에게 정확히 도달한다.
다음은 송신자에 대한 큐잉 모델(Queueing model for Transmitter)이다.
- 무한 버퍼: 송신자는 임시로 패킷을 저장할 수 있는 무한 버퍼를 소유한다. 전송 대기 중인 패킷이 많아도 저장 공간에는 제한이 없다.
- 패킷 도착 시 처리: 패킷이 송신자에 도착하면, 송신자는 버퍼의 가장 아래에 패킷을 저장한다.
- 패킷 전송 규칙: 송신자는 버퍼의 맨 위에 있는 패킷을 전송한다(FCFS).
- ACK 수신 시 처리: 송신자가 ACK을 수신하면, 버퍼의 맨 위에 있는 패킷을 제거한다. 즉, 전송이 성공적으로 이루어진 것으로 간주한다.
위의 송신자 큐잉 모델을 분석해보자.
먼저, 패킷의 재전송 횟수에 대한 분석이다.
$N^{(k)}_{RT}$는 송신자가 k번째 패킷을 수신자가 오류 없이 수신할 때까지 재전송하는 횟수를 나타낸다.
이 값은 기하 분포를 따르며, 매개 변수는 $p_P$이고, 다음의 확률 분포식을 가진다.
$$P(N^{(k)}_{RT} = k) = (1 - p_P)p^k_P$$
k = 0일 경우, 첫 번째 시도에서 성공적으로 수신되었음을 의미한다.
여기서 $N^{(1)}_{RT}, N^{(2)}_{RT}$ ... 는 상호 독립적이며, 동일한 분포를 따른다.
여기서부터는 재전송하는 횟수를 $N_T$로 줄여서 표현해보겠다.
$N_T$의 예상되는 값은 어떻게 계산되냐면...
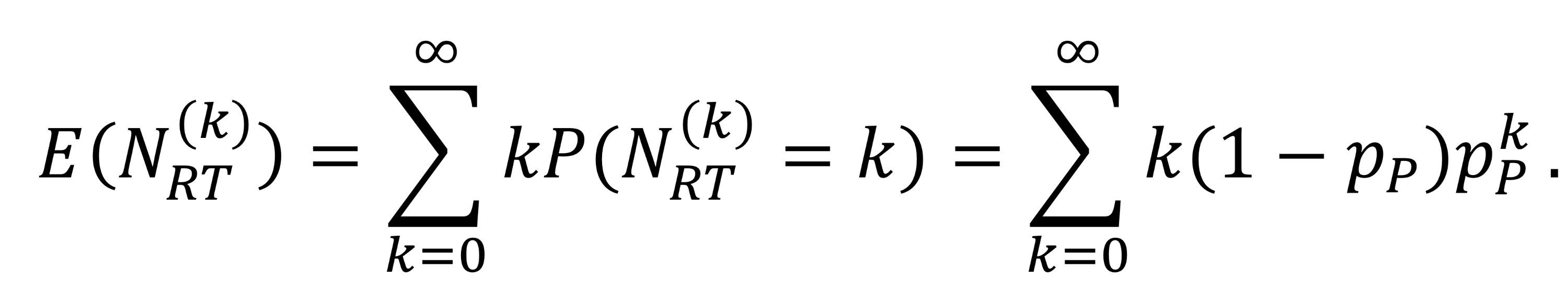
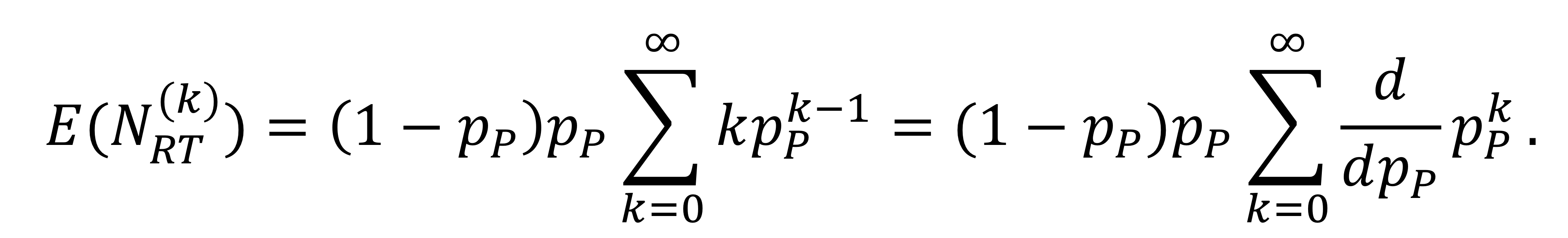
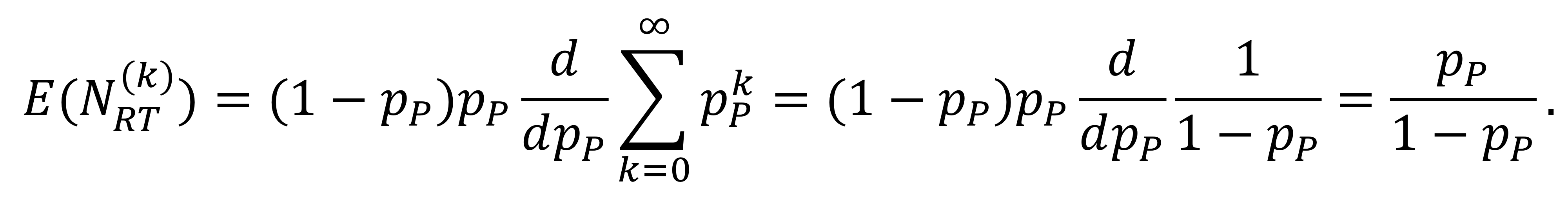
이런 식들을 통해 $E(N_T) = \frac{p_P}{1 - p_P}$가 된다.
다음은 큐의 맨 위에서의 체류 시간(Sojourn Time at the Top of th Buffer)에 대한 분석이다.
패킷이 큐의 맨 위에 도달한 순간부터 해당 패킷이 제거될 때까지의 시간을 체류시간이라고 한다.
$S^{(k)}$는 k번째 패킷의 체류 시간을 나타내고, 이는 다음과 같이 표현된다.
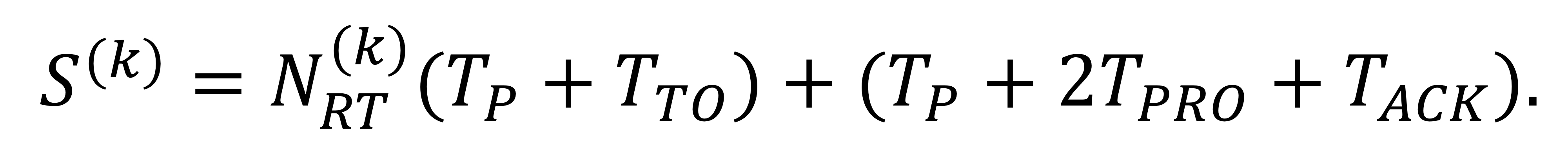
최적의 타임아웃 기간을 사용한다고 가정하면, 다음과 같이 표현된다.
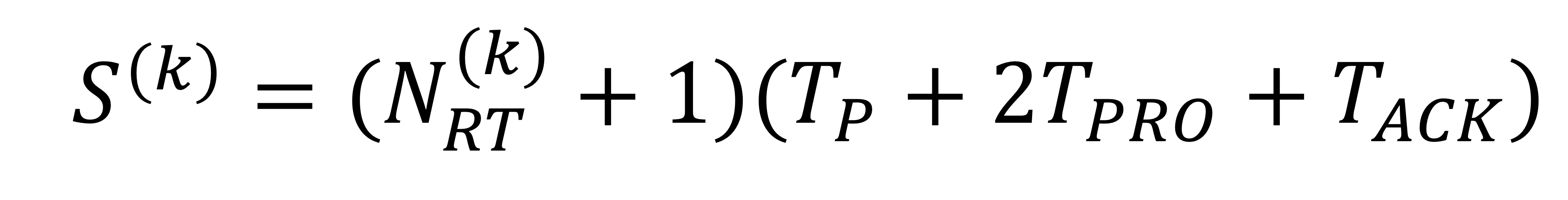
$S^{(1)}, S^{(2)}$... 는 역시나 상호 독립적이며 동일한 분포를 따른다.
$E(S^{(k)})$의 값은 다음과 같은 식으로 계산할 수 있다.
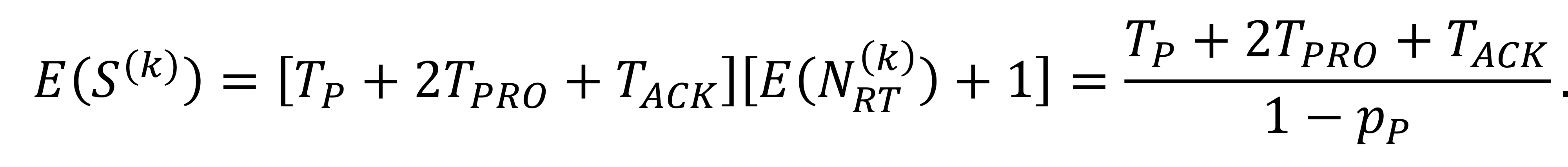
자, 이제 처리량을 분석해보자.
결론부터 말하자면, $\frac{1}{E(S^{(k)})}$가 처리량이다. 왜 이렇게 되는지 알아보자.
$N_t$는 시간 구간 (0, t] 동안 수신자가 수신한 오류 없는 패킷의 수를 나타낸다. 따라서 처리량($\eta$)는 다음과 같이 표현된다.
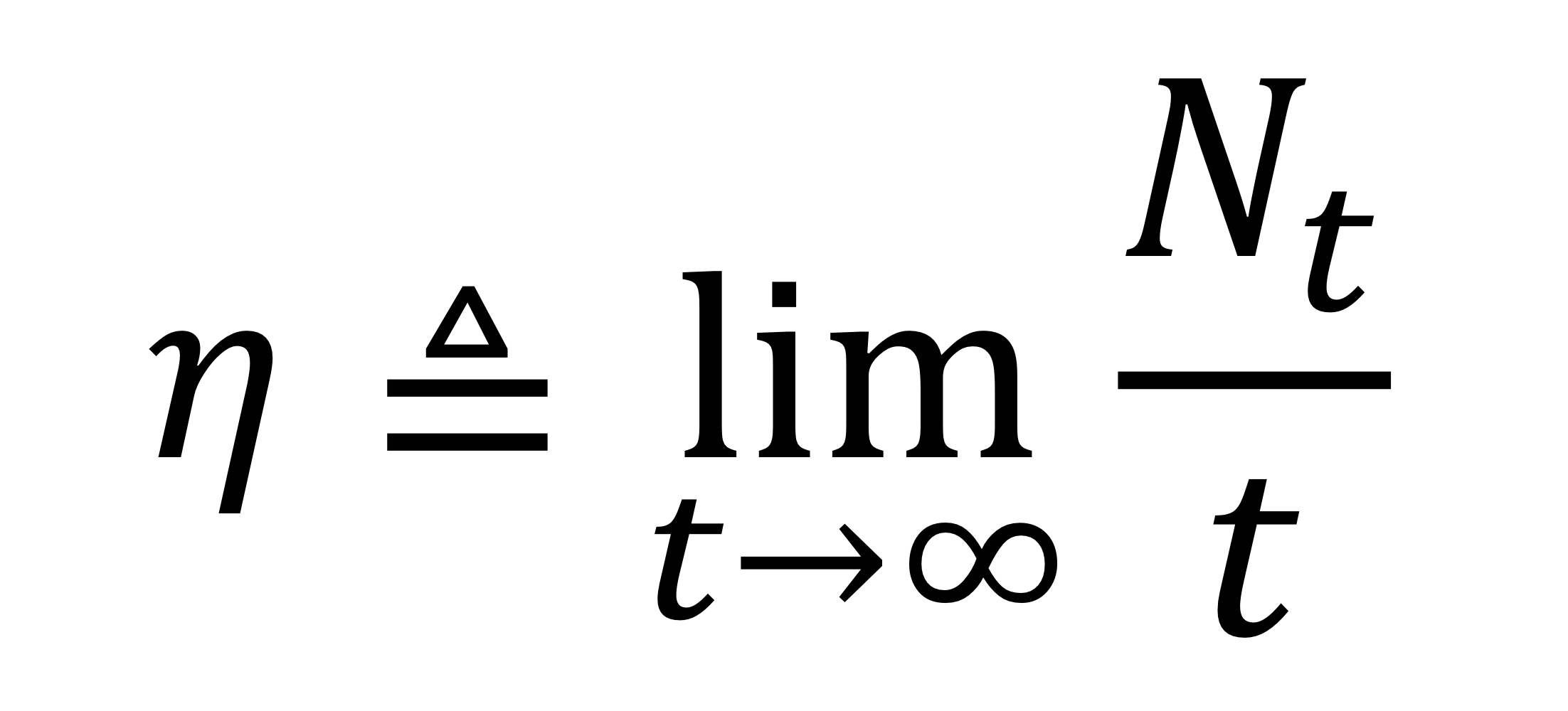
이는 단위 시간 당 오류가 없는 패킷이 수를 의미한다.
송신자가 포화 상태인 경우, 수신자는 각 체류시간 동안 하나의 오류 없는 패킷만 수신한다.
이 경우, 포화 처리량은 다음과 같이 표현할 수 있다.
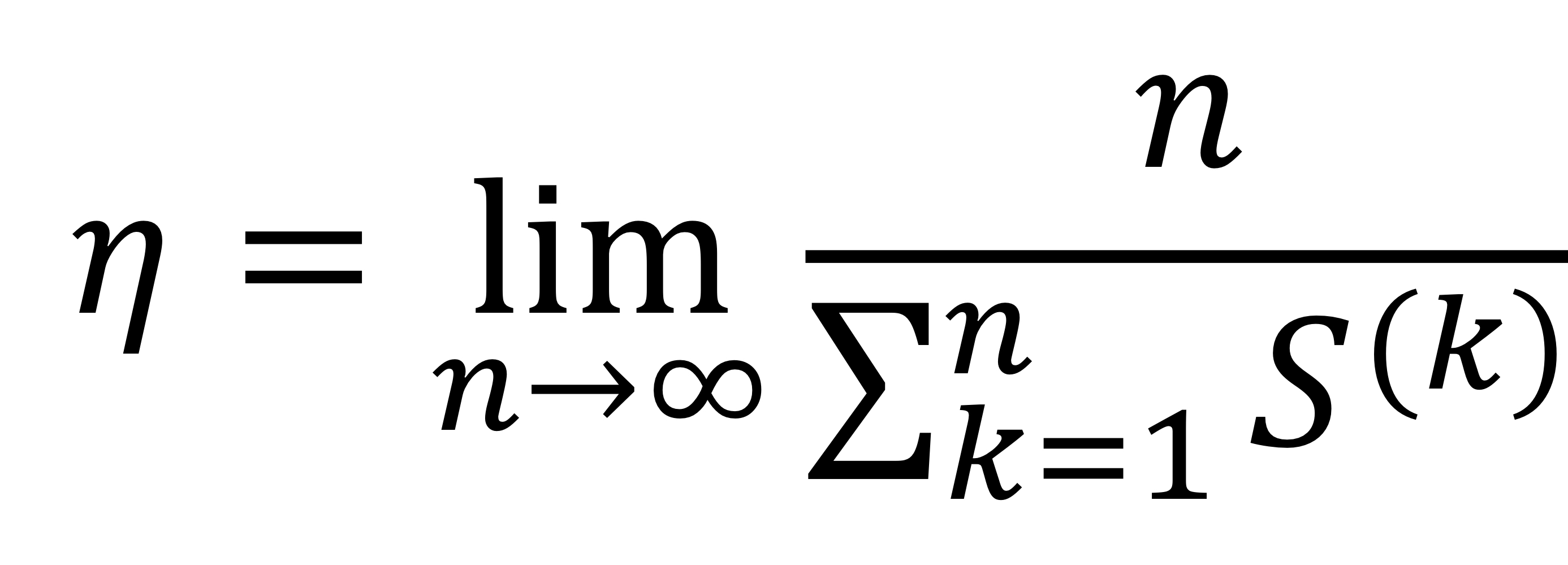
위 식은, $\eta = \frac{1}{E(S^{(k)})}$로 표현할 수 있다.
여기서 송신자가 최적의 타임아웃 기간을 사용한다면, 포화 상태 처리량은 다음과 같이 표현된다. (packets/unit time)
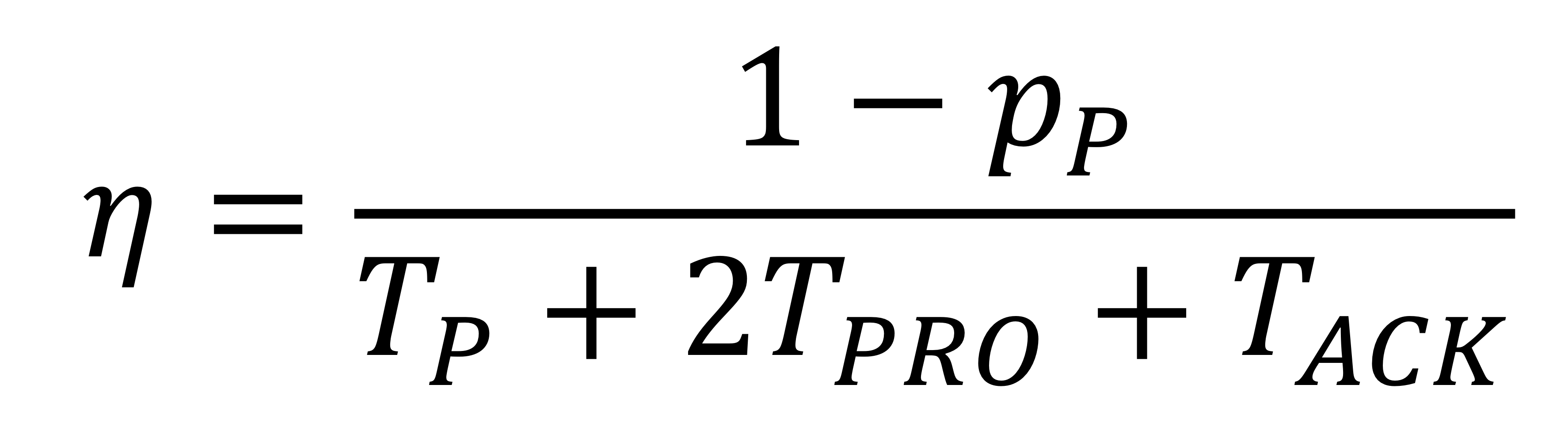
자, 이제 위 포화 상태의 처리량 식을 기본 매개 변수를 사용하여 다음과 같이 재작성할 수 있다. (bits/sec)
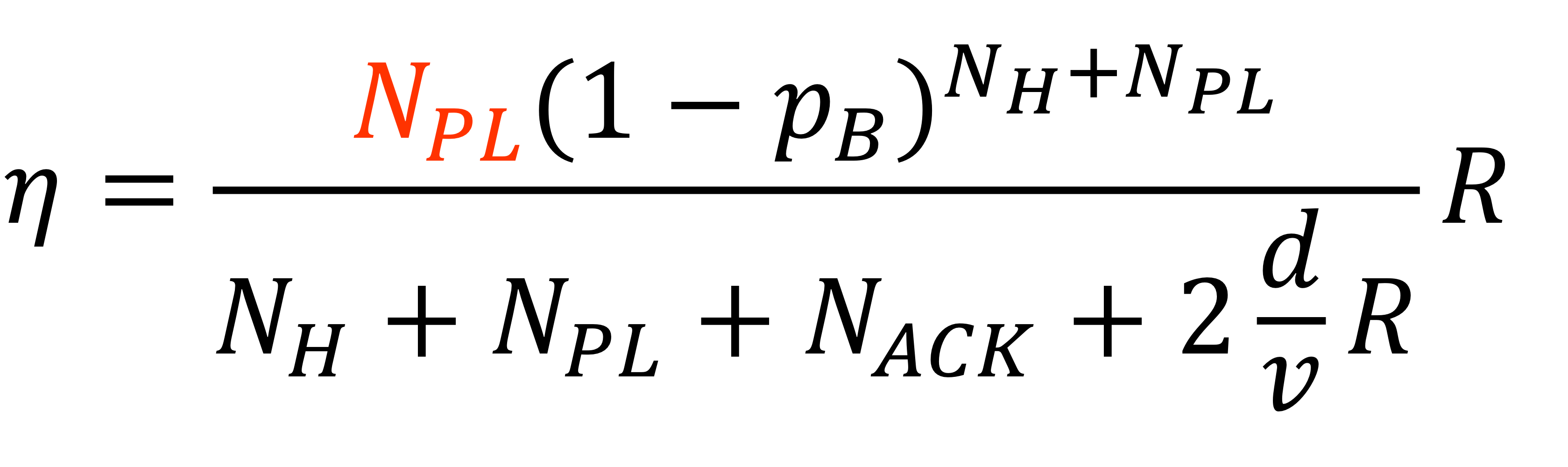
여기서 $p_B$는 비트에서 오류가 발생할 확률이다.
이 식에서 우리는 normalized saturated throughput, 정규화된 포화 상태의 처리량(~$\eta$) 식을 구할 것이다. (bits/bit transmission time)
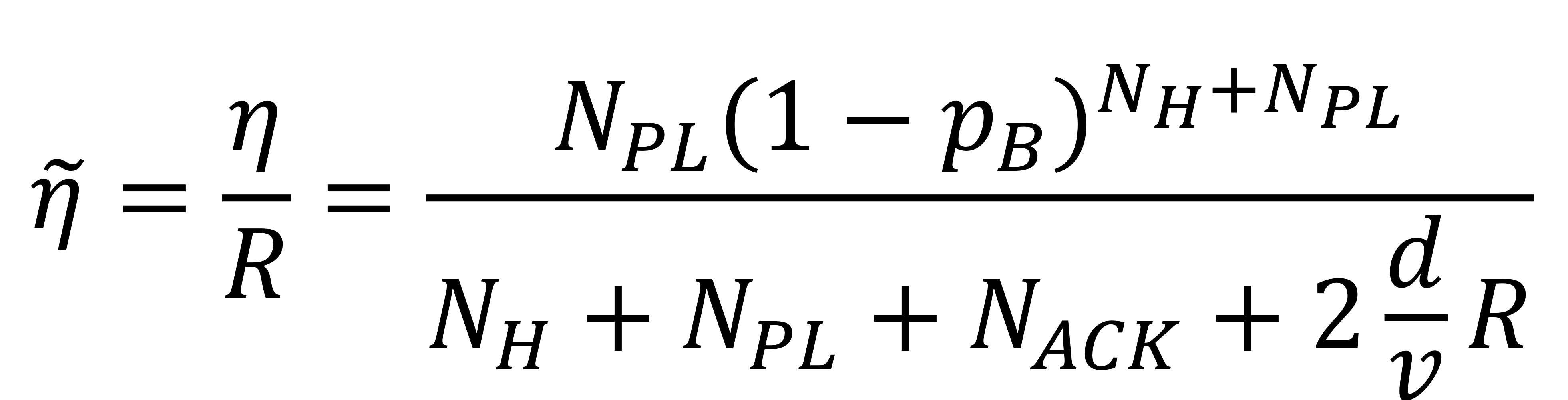
Numerical example: 수치 예시
- 정규화된 포화 상태의 처리량 vs 비트 오류 발생 확률
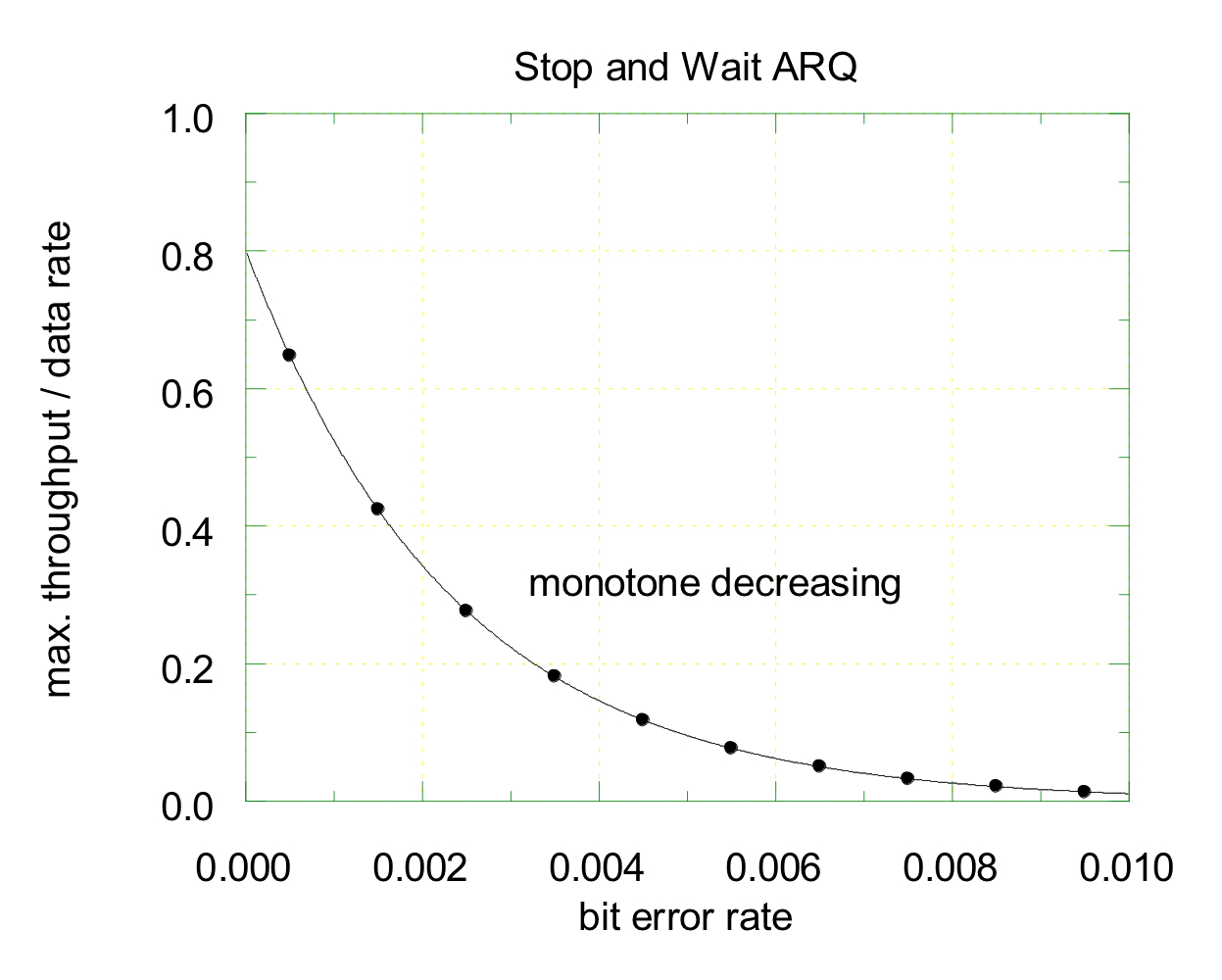
정규화된 포화 상태의 처리량은 비트 오류율이 증가함에 따라 감소한다.
비트 오류율이 증가하면, 패킷 오류율 또한 증가하게 된다. 그러면 비트 오류율이 증가할수록 패킷을 재전송할 확률이 높아진다. 즉, 비트 오류율이 높아질수록 평균적으로 재전송 횟수가 증가한다는 것이다. 이로 인해 전송 성능이 저하되고, 전체 시스템의 처리량이 감소하게 된다.
- 정규화된 포화 상태의 처리량 vs 거리
정규화된 포화 상태의 처리량은 거리가 증가함에 따라 감소한다.
거리가 증가할 수록, 송신자와 수신자 사이의 전파 지연 시간이 길어진다. 이는 패킷이 목적지에 도달하거나 응답이 돌아오는데 걸리는 시간이 증가함을 의미한다. 따라서 거리 증가는, 최적 타임아웃 기간을 늘리게 된다. 최적 타임아웃 기간이 늘어날수록 패킷이 송신자 큐에서 평균적으로 체류하는 시간이 증가하며, 이는 전송 및 재전송 과정에서의 지연으로 연결되고, 결국 처리량을 저하시킬 수 있다.
- 정규화된 포화 상태의 처리량 vs 데이터 전송 속도
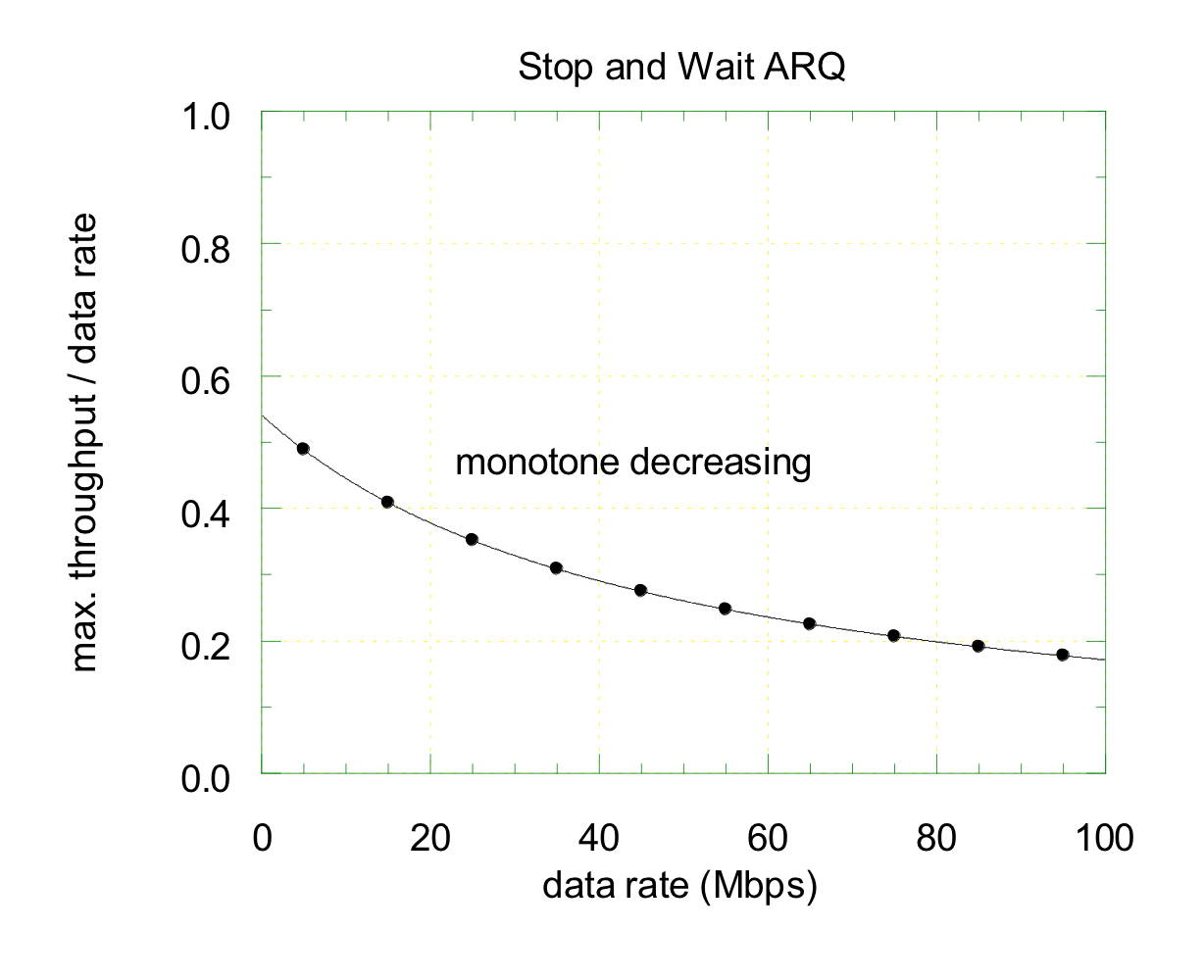
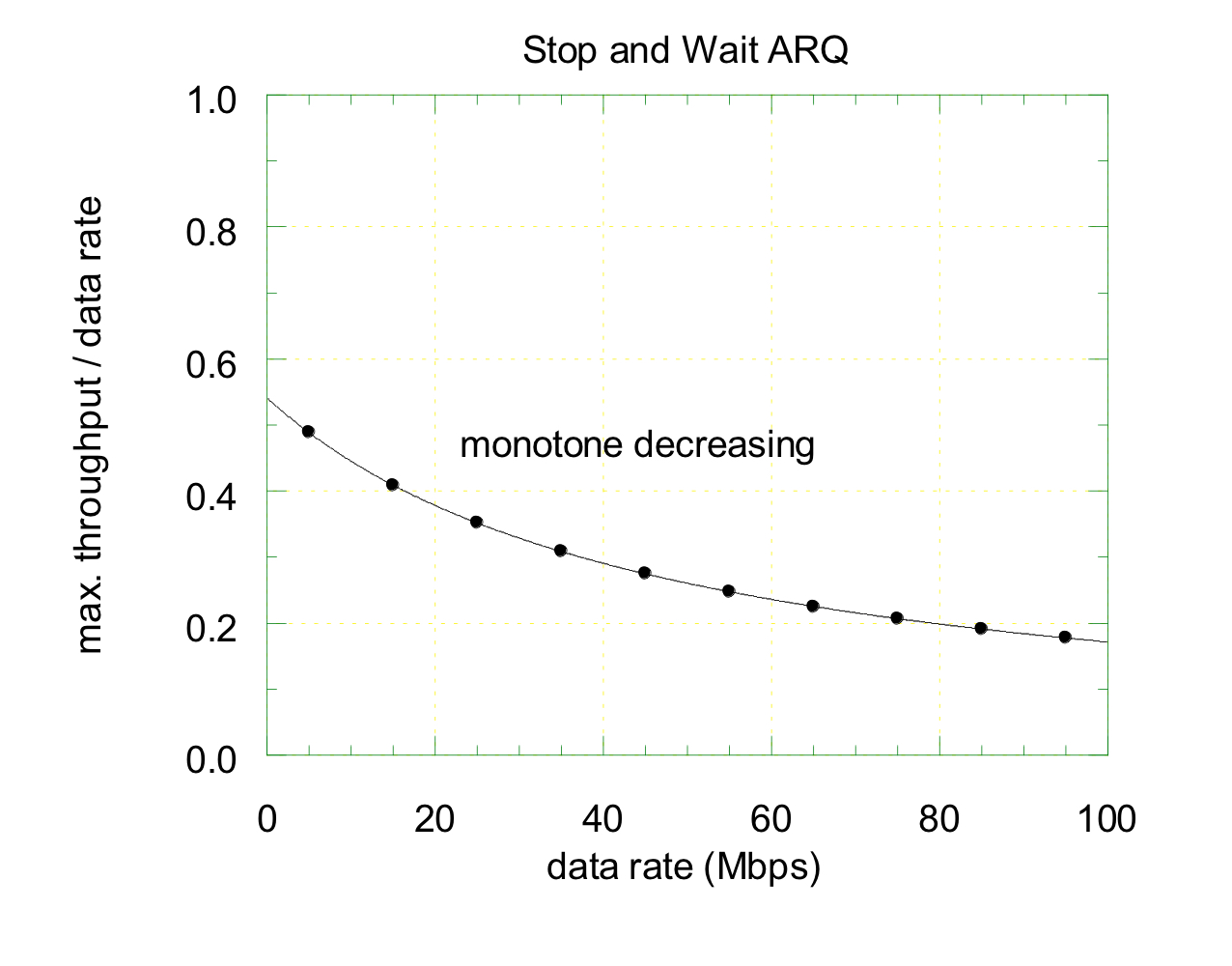
정규화된 포화 상태의 처리량은 데이터 전송 속도가 증가할수록 감소한다.
그러나 데이터 전송 속도가 일정 수준 이상으로 증가하면, 처리량이 수렴하는 값에 가까워진다. 이러한 결과는 Stop and Wait ARQ 방식이 고속 네트워크에서는 비효율적임을 나타낸다.
데이터 전송 속도가 증가하면, 패킷 전송이 빠르게 이루어지지만, Stop and Wait ARQ방식은 각 패킷 전송 후 ACK을 기다려야하기 때문에 상대적으로 대기 시간이 증가한다. 여기서 데이터의 전송 속도가 매우 높아지면, 전파 시간만을 고려할 수 있게 되어 처리량이 특정 수치에 수렴한다.
- 정규화된 포화 상태의 처리량 vs 페이로드의 길이
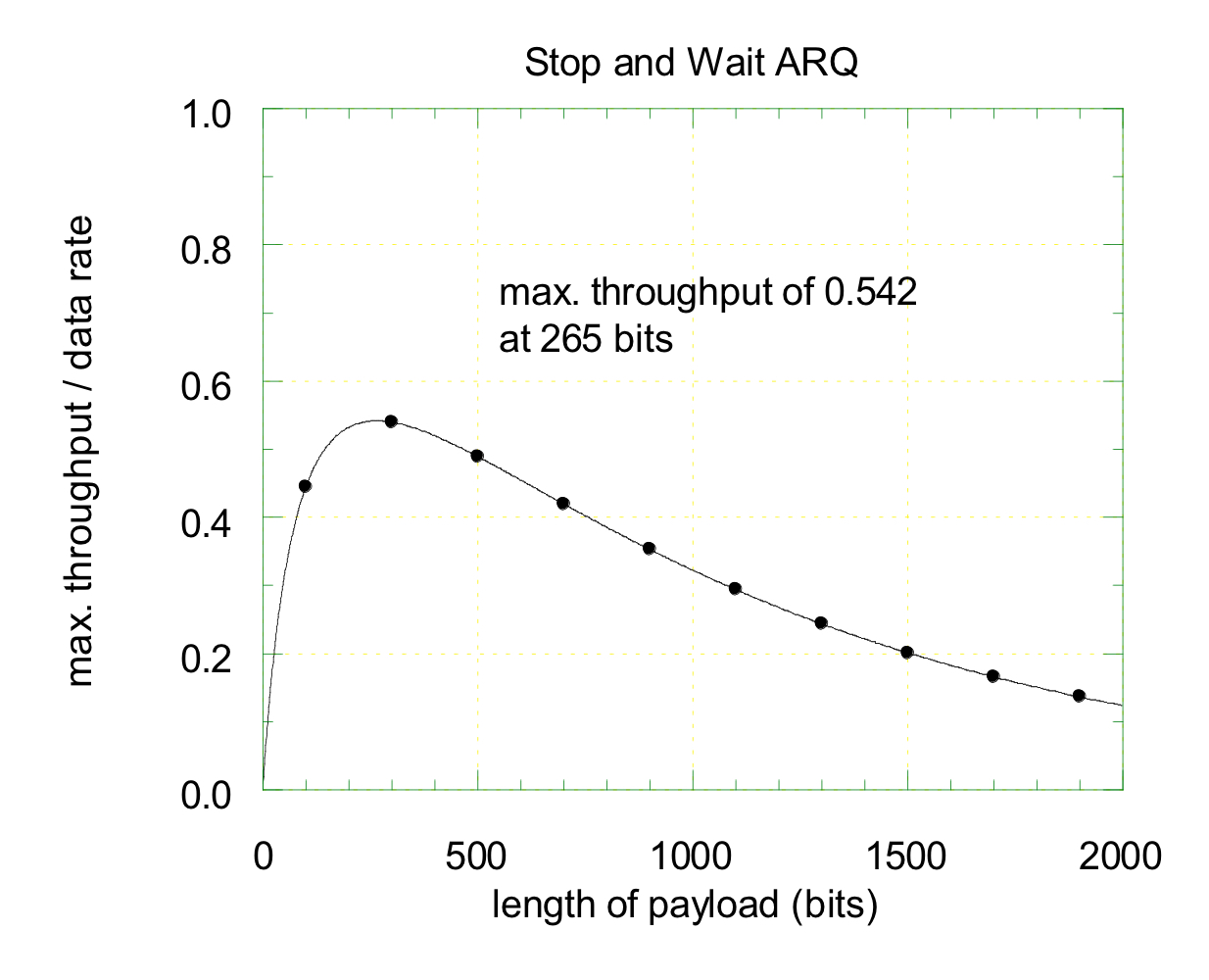
특정 페이로드 길이에서 처리량 효율이 최대화된다.
페이로드의 길이가 증가할수록 전체 패킷의 길이도 증가하므로 패킷 오류율이 증가한다. 또한 페이로드의 길이가 길어지면 헤더 및 기타 오버헤드에 비해 전송 데이터의 비율이 커지므로, 오버헤드 비효율성이 감소한다. 이는 처리량 개선에 기여할 수 있지만, 오류 발생 위험이 커진다. 따라서 페이로드 길이의 변화는 패킷 오류율과 오버헤드 비효율성 간의 트레이드 오프를 발생시킨다.
아.. 중간고사가 끝나고 모든 과목들의 난이도가 급격하게 올라가기 시작했다.
나는 .. 여기까지인가.
** 대학교 수업을 듣고 이해한 부분을 최대한 풀어서 작성한 글입니다.
틀린 정보가 존재할 수 있으며, 언제나 피드백은 환영입니다. **
'DKU > 데이터 통신' 카테고리의 다른 글
| Error Control 3 (0) | 2024.11.14 |
|---|---|
| Error Control 2 (7) | 2024.11.13 |
| Multiple Access 2 (0) | 2024.10.22 |
| Multiple Access (0) | 2024.10.16 |
| Multiplexing 2 (0) | 2024.10.01 |
