Random access (No Schedule)
ALOHA
알로하는 하와이 대학교에 있는 Norman의 팀이 4개의 섬에 있는 7개의 컴퓨터의 통신을 어떻게 간단하게 수행할 수 있을까에 대해 찾다가 만들었다.
7개의 스테이션이 서로 패킷을 교환하는데, 패팃의 구조는 헤더(32비트), 패리티 검사(16비트), 데이터(80바이트), 패리티 검사(16비트)로 이루어져있다. 중앙 스테이션인 Menehune은 다른 모든 스테이션으로 패킷을 보내기 위해 전방 채널(Forward channel)을 사용한다. 이 채널은 413.475 MHz를 중심으로 하고, 100kHz의 대역폭을 가진다. 다른 스테이션들은 407.350MHz를 중심으로 하고, 100kHz 대역폭을 가지는 역방향 채널(Reverse channel)을 공유하여 Menehune에 패킷을 전송한다.

위 사진을 보면 패킷을 전달하고 Time-out period를 기다린다.
이 Time-out period는 외부 스테이션이 패킷을 전송한 직후 시작되는 시간 간격을 의미한다.
외부 스테이션이 중앙 스테이션에 패킷 전송을 완료했다고 가정하면, 타임아웃 기간이 시작된다. 이 타임 아웃 기간동안, 외부 스테이션은 중앙 스테이션으로부터 해당 패킷의 수신을 확인하는 Acknowledgement(승인)을 기다린다.

- 패킷 전송 시간: $T_p$
- ACK 전송 시간: $T_{ACK}$
- 전달 지연: $T_{PRO}$
- 타임아웃 기간의 길이: $T_{TO}$
- 타임아웃 기간의 최적 시간: $T^{*}_{TO}$
위의 표기법을 사용한다고 하면, 타임아웃 기간의 최적 시간을 구하는 공식이 나온다.
$$T^{*}_{TO} = 2T_{PRO} + T_{ACK}$$
중앙 스테이션으로부터 ACK을 받지 못하고, 외부 스테이션이 이전 패킷 전송에 실패했다고 판단한 순간부터 Back off-time이 시작된다. 백오프 시간은 해당 스테이션이 패킷 재전송을 시작하기까지의 경과 시간이 된다.
외부 스테이션은 백오프 시간 동안 잠시 대기해야하며, 이는 패킷 충돌이 반복되는 가능성을 줄이기 위함이다.
백오프 시간은 반드시 임의(random)로 설정되어야 하며, 두 가지 방식이 존재한다.
- Truncated binary exponential back-off scheme(잘린 이진 지수 백오프 방식): 재전송을 시도할 때마다 백오프 시간이 지수적으로 증가하다가 특정 지점에서 제한되는 방식
- p-persistence back-off scheme(p-지속성 백오프 방식): 재전송을 시도할 때마다 일정 확률 p에 따라 재전송을 결정하는 방식

잘린 이진 지수 백오프 방식은, 외부 스테이션이 패킷 전송에 연속해서 n번 실패했다고 판단한 상황을 가정한다.
외부 스테이션이 n번째 전송 시도에 실패했다고 판단한 순간부터, n번째 패킷 재전송을 시작하기 전에 백오프 시간을 기다린다.
백오프 시간은 다음과 같이 설정된다.
$$T^{(n)}_BO = T_P ・ K_n$$
여기서 $T_P$는 일정한 시간 간격이며, $K_n$은 {0, 1, ... $2^{n-1}$} 사이에서 균일하게 분포된 랜덤 변수이다.
외부 스테이션이 패킷 전송에 연속해서 $\gamma$번 실패했다고 판단하면, 패킷 전송을 포기한다.
이 방식은 백오프 시간이 랜덤하게 설정되기 때문에, 충돌을 줄이면서 재전송을 시도를 조정하는 효과가 있다. 또한, n번째 재전송을 할 때마다 백오프 시간이 지수적으로 증가하며, 재전송 시도가 일정 횟수를 넘으면 패킷 전송을 포기하는 메커니즘을 가지고 있다.
p-지속성 백오프 방식 역시 외부 스테이션이 패킷 전송에 연속해서 n번 실패했다고 판단한 상황을 가정한다.
이 역시 n번째 전송 시도에 실패했다고 판단한 순간부터, n번째 패킷 재전송을 시작하기 전에 백오프 시간을 기다린다.
백오프 시간은 다음과 같이 설정된다.
$$T^{(n)}_BO = T_P ・ K$$
여기서의 $T_P$도 일정한 시간 간격이며, $K$는 매개변수 1-p를 갖는 기하 분포를 따르는 랜덤 변수이다.
즉, 이 방식에서 백오프 시간은 기하 분포에 따라 랜덤하게 설정되며, 매개변수 p는 재전송을 제어하는 확률을 나타낸다. 기하 분포는 이벤트가 발생할 때까지 실패 횟수를 모델링하므로, p가 높을수록 재전송은 더 빠르게 일어난다.
ALOHA의 처리량 성능
중앙 스테이션이 시간 $t_0$에 패킷 P1을 수신하기 시작했다고 가정한다.
다른 패킷 P2가 시간 간격 $V = (t_0 - T_P, t_0 + T_P)$동안 중앙 스테이션에 도착하기 시작했다.
그러면 패킷 P1과 P2는 Collision(충돌)하게 된다.

이 시간간격 V를 vulnerable periods, 취약 기간이라고 부른다. 이 시간 동안에는 충돌이 발생할 확률이 매우 높다.
강도(intensity) $\lambda$를 가지는 Possion point process는 {$A_n: n = 0, 1, ...$}로 표시되는 일련의 시간들로 정의된다.
$A_0$ = 0는 거의 확실하게 성립한다. 즉, $A_0$는 항상 0이라고 볼 수 있다.
$A_1 - A_0, A_2 - A_1$ ... 는 서로 독립적이므로, 각 간격 사이의 시간이 서로 연관이 없다.
모든 n에 대해, $A_n - A_{n-1}$은 매개변수 $\lambda$를 가지는 지수 분포를 따른다. 즉, 확률 $P(A_n - A_{n-1}) \leq x)$는 다음과 같이 정의된다.
$$P(A_n - A_{n-1}) \leq x) = 1 - e^{-\lambda・x}$$
즉, possion point process는 사건이 시간이 지남에 따라 발생하는 확률적 모델로, 각 사건 사이의 시간이 지수 분포를 따르며 강도 $\lambda$는 사건이 발생하는 빈도를 나타낸다.
강도 $\lambda$를 가지는 Possion counting process는 ${N_t : t \geq 0}$으로 표시되며, 연속적으로 발생하는 사건을 세는 확률적 과정이다.
$N_0$ = 0는 거의 확실하게 성립된다. 즉, t = 0일 때 사건이 발생하지 않음을 의미한다.
$N_t : t \geq 0$은 정상이며, 독립적인 증가분을 가진다. 즉, 시간 간격 내의 사건 수는 서로 독립적이고 일정한 속도로 발생한다.
모든 t에 대해, $N_t$는 매개변수 $\lambda・t$를 가지는 possion 분포를 따른다. 즉, $P(N_t = n)$은 다음과 같이 정의된다.
$$P(N_t = n) = \frac{e^{-\lambda・t}(\lambda・t)^n}{n!}$$
이는 시간 t 동안 n개의 사건이 발생할 확률을 나타낸다.
$0<a<b<\infty$ 인 구간 (a, b]동안 발생한 사건의 개수는 다음과 같은 확률 질량 함수를 가진다.
$$P(N_b - N_a = n) = \frac{e^{-\lambda(b-a)}[\lambda(b-a)]^n}{n!}$$
Possion counting process는 시간이 지남에 따라 사건이 발생하는 빈도를 설명하는 확률 과정이며, $N_t$는 특정시간 t까지 발생한 사건의 수를 나타낸다.
중앙 스테이션의 패킷 도착은 비율 g(packets/sec)인 Possion 과정을 따른다고 한다.
$p_{COL}$은 패킷이 다른 패킷들과 충돌할 확률을 나타낸다.
충돌 확률 $p_{COL}$은 취약기간 동안 적어도 하나의 패킷이 도착하는 확률로 정의된다. 그리고 이는 패킷이 취약 기간 V 동안 전혀 도착하지 않는 확률을 빼서 계산할 수 있다.
$p_{COL}$ = P(At least on packet arrives in V) = 1-P(No packet arrives in V)
취약 기간 V의 길이는 2$T_p$이므로, 패킷이 도착하지 않는 확률은 Possion 과정에 의해 $e^{-2gT_{p}}$로 표현된다.
따라서 충돌 확률 $p_{COL}$은 다음과 같이 정의된다.
$$p_{COL} = 1 - e^{-2gT_{p}}$$
패킷이 중앙 스테이션 비율 g(pacekts/sec)로 도착한다고 한다.
각 패킷은 다른 패킷들과 독립적으로 충돌할 확률 $p_{COL}$을 가지며, 충돌하지 않을 확률은 $1 - p_{COL}$이다.
따라서, 네트워크 전체 처리량 $\eta$(packets/sec)은 충돌하지 않고 성공적으로 전송되는 패킷의 비율로 나타낼 수 있으며, 다음과 같이 표현된다.
$$\eta = g(1 - p_{COL}) = ge^{-2gT_{p}}$$
중앙 스테이션은 한 번의 패킷 전송 시간 동안 하나 이상의 패킷을 수신할 수 없다.
정규화된 네트워크 처리량 $\eta *$은 패킷 전송 시간 당 패킷(패킷/패킷전송시간)으로 나타낼 수 있다. 이는 다음과 같이 표현된다.
$$\eta * = ge^{-2gT_{p}}・T_p = Ge^{-2G}$$
여기서 $G = gT_p$는 패킷 도착률과 패킷 전송 시간의 곱이다.
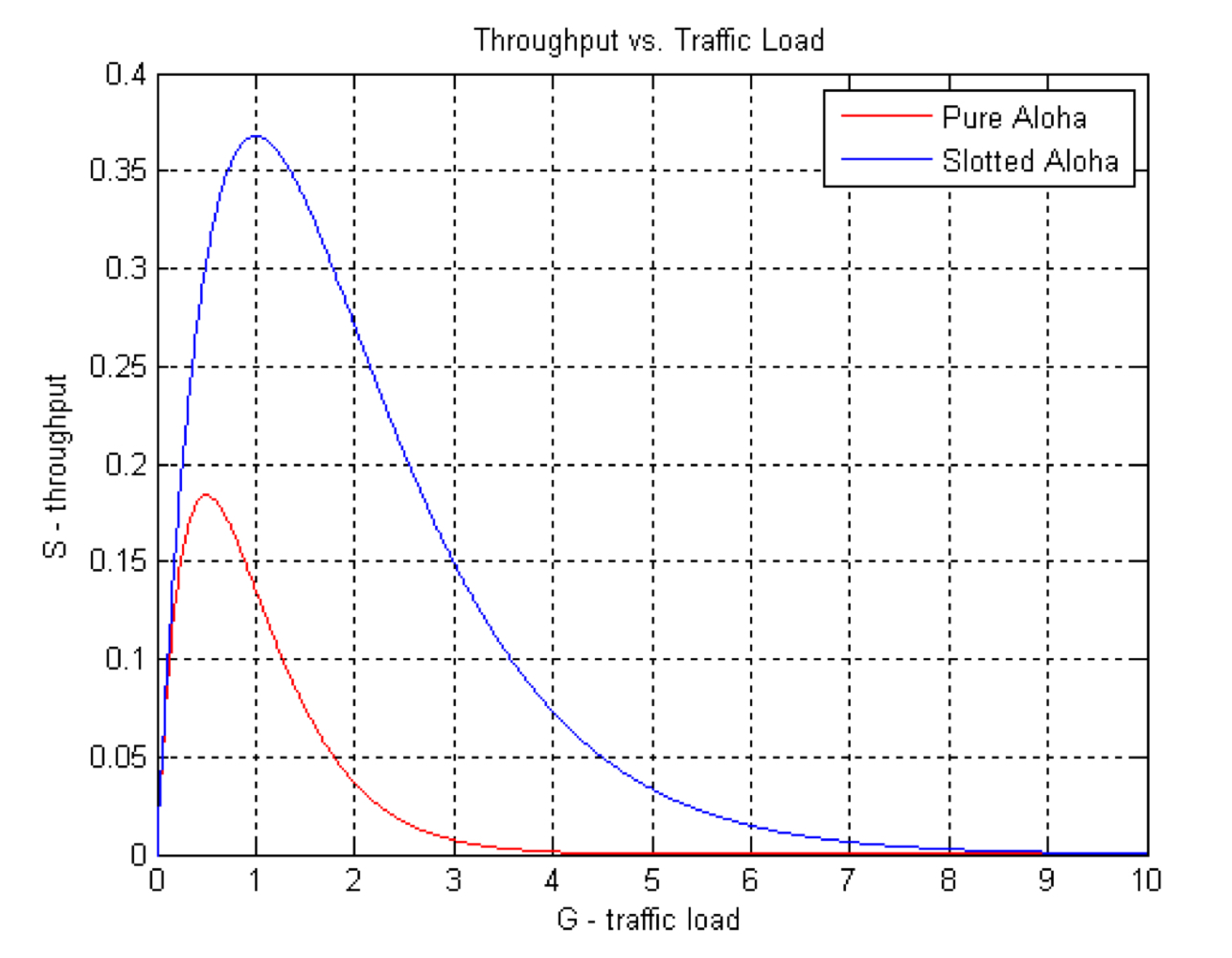
정규화된 네트워크 처리량 식을 미분을 하고, 기울기가 0이 되는 부분을 찾으면 G = 1/2 일 때가 나온다.
이는 정규화된 네트워크 처리량이 G=1/2일 때 최대가 된다는 의미이다.
따라서 G에 1/2를 대입해보면, 어림잡아 0.184라는 값이 나온다.
교수님께서 시험 전날까지 진도를 나가시려는 무시무시한 생각을 하고 계신다. 당근을 흔들자.
** 대학교 수업을 듣고 이해한 부분을 최대한 풀어서 작성한 글입니다.
틀린 정보가 존재할 수 있으며, 언제나 피드백은 환영입니다. **
'DKU > 데이터 통신' 카테고리의 다른 글
| Error Control 2 (7) | 2024.11.13 |
|---|---|
| Error Control (2) | 2024.11.12 |
| Multiple Access (0) | 2024.10.16 |
| Multiplexing 2 (0) | 2024.10.01 |
| Multiplexing (4) | 2024.09.30 |
