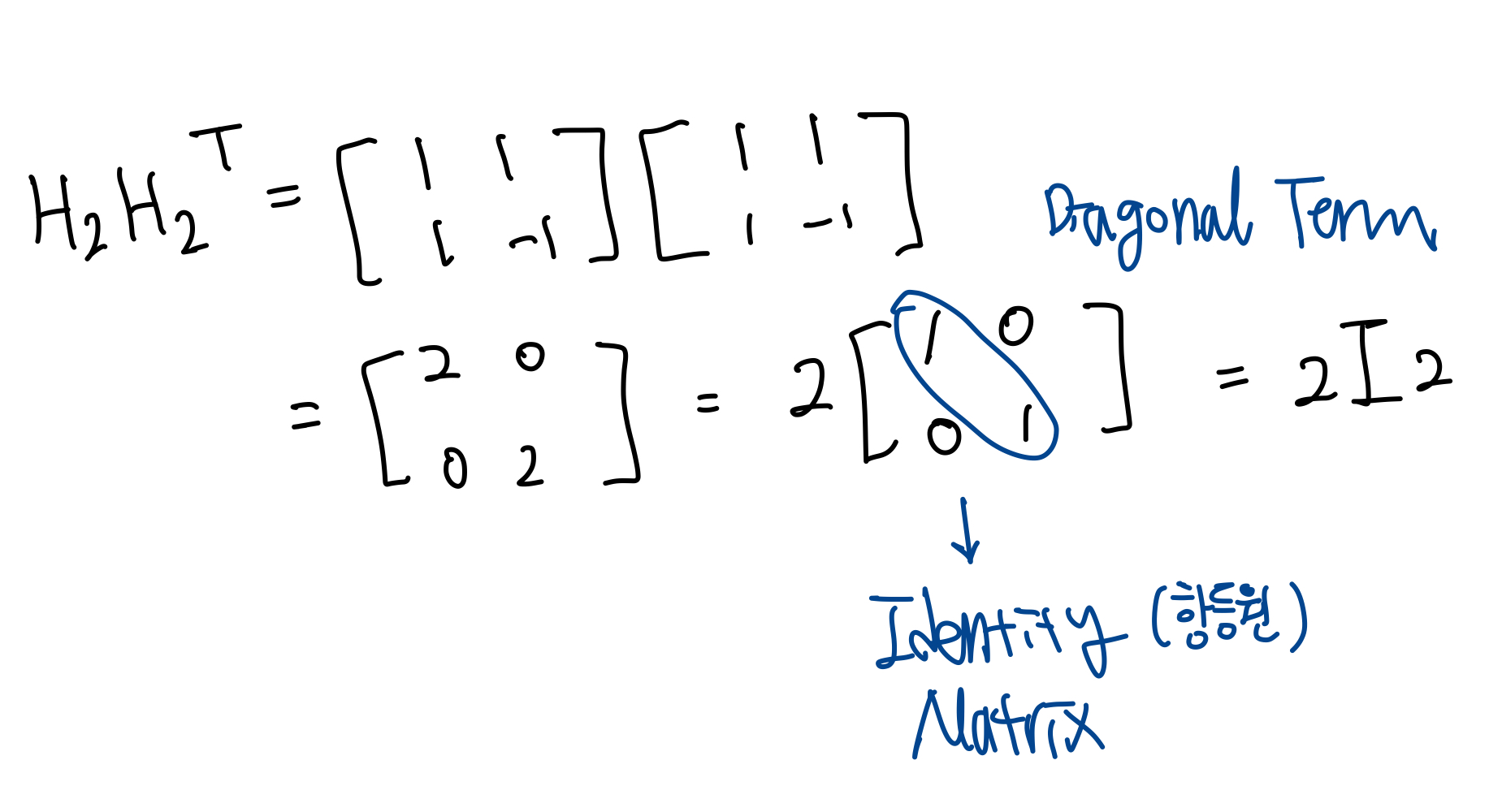CDM(Code Division Multiplexing): 코드 분할 다중화
CDM은 각 채널이 고유한 직교함수 또는 코드워드를 사용하여 데이터를 전송하는 방식이다.
- 직교함수(orthogonal function): 서로 다른 채널들이 서로 간섭하지 않도록 하기 위해 사용하는 고유한 코드나 신호 패턴이다. 직교 함수는 서로 독립적이기 때문에, 하나의 채널에서 전송된 신호는 다른 채널에서 전송된 신호와 겹치지 않는다.
Hadamard matrix
하다마드 행렬은 모든 요소가 +1 또는 -1로 이루어진 정사각 행렬이며, 행과 열이 서로 직교하는 특별한 성질을 가지고 있다.
이 직교성은 다음과 같은 조건을 만족한다.
$$H_{n}H_{n}^T = nI_{n}$$
즉, 하다마드의 행렬의 행과 열은 서로 직교하며, 그 결과 두 벡터의 내적이 0이거나, 벡터가 자신일 때는 행렬의 차수(n)와 같다.

Orthogonal basis
선형 대수에서 벡터들이 서로 직교(orthogonal)하는 경우를 말한다.
즉, 기저를 이루는 벡터들 간의 내적(inner product)이 0인 상태이다.
- 내적이란, 벡터와 벡터 사이의 곱셈 연산으로, 두 벡터 간의 유사성이나 관계를 측정하는 방법 중 하나다.
- 벡터A[2 3], 벡터 B[4,1]의 내적은 (2×4) + (3×1) = 11 이다.
하다마드 행렬에서 차수가 4인 행렬을 보겠다.
$H_4$는 다음과 같이 4개의 행으로 구성되어 있다.

$h_ij$는 $H_4$에서 j번째 행, i번째 열을 뜻한다.
여기서 $C_1, C_2, C_3, C_4$는 서로 직교하는 성질을 가지고, 코드워드라고 할 수 있다.
자기 자신이 아닌 행렬과 내적을 구하면 무조건 0이된다. ($C_1C_1$은 4로, 0이 아님)

위 내용을 시그널로 변환해보자면,
$\Phi_1(t)$, $\Phi_2(t)$, $\Phi_3(t)$, $\Phi_4(t)$로 표시된 4개의 기저 함수를 만든다.
각 시그널은 4개의 직사각형 펄스로 구성되며, 각 펄스의 넓이는 $\frac{\tau}{4}$다.
시그널$\Phi_i(t)$를 포함하는 4개의 펄스의 높이는 $h_i1, h_i2, h_i3, h_i4$이며, i $\in$ {1,2,3,4} 이다.

이 신호는 각기 다른 직교 기저 함수로, 서로 직교하므로 다른 신호 간에 간섭이 없다는 것이 특징이다.
즉, 각 신호가 독립적으로 전송될 수 있으며, 이는 여러 사용자가 동일한 주파수 대역을 공유하면서도 각 사용자가 구분될 수 있게 해준다.
CDM은 직교함수를 이용하여 어떤 방식으로 작동할까?
두 개의 스테이션 A와 B가 CDM으로 비트 스트림을 전송한다고 하자.
스테이션 A는 비트 스트림{1,0}, 스테이션 B는 비트 스트림{0,1}을 전송한다.
CDM은 1/$\tau$(bps)의 속도로 출력 링크를 통해 비트 스트림을 전송한다고 가정한다.
또한, CDM이 스테이션 A에는 $C_2$를, 스테이션 B에는 $C_3$를 할당할 것이다.

같은 코드워드를 사용하면 안된다는 것은 위 내용을 통해 배웠다.
$C_2$ = [1 -1 1 -1] 이며, $C_3$ = [1 1 -1 -1]이다.
스테이션 A의 비트 스트림을 먼저 변환해보자.
각각의 비트{1, 0}에 $C_2$를 곱해주면 되는데, 이 때 비트0은 -1로 바꿔서 계산해준다.
- 0을 -1로 변환하는 이유는, 신호를 효율적으로 처리하고 수학적 연산을 쉽게 하기 위해서다. 0을 -1로 변환하게 되면, 신호는 대칭적인 파형을 가지게 되는데, 이 대칭성은 신호를 더 쉽게 처리하고 신호 복원을 간편하게 해준다. 또한 모든 비트를 +1과 -1로 이루어지게 하면서 신호의 에너지 소비 균형을 맞출 수 있게된다.
코드워드를 곱하게 되면, {+1 -1 +1 -1 / -1 +1 -1 +1}이 된다.
이 때 각각의 bit를 chip이라고 부르는데, 총 8개의 chip이 생성된 것이다.
위와 같은 방식으로 스테이션 B의 비트 스트림을 변환하면 {-1 -1 +1 +1 / +1 +1 -1 -1}이 된다.
이제 스테이션 A의 chip들과 스테이션 B의 chip들을 더하게 되면, {0 -2 2 0 / 0 2 -2 0}의 신호가 만들어지는데, 이 신호를 전송시키게 되는 것이다.
이 신호를 해석하는 디멀티플렉서에서는 전송받은 신호에 코드워드를 곱해서 해석을 진행한다.
스테이션 A의 비트 스트림을 얻으려면, 전송받은 신호 {0 -2 2 0 / 0 2 -2 0}에 각각 $C_2$를 곱해준다. (1 -1 1 -1 / 1 -1 1 -1)
결과값으로 {0 2 2 0 / 0 -2 -2 0}이 나오는데, 첫 번째 비트의 chip들을 더해보면 4, 즉 양수로 1이라는 bit가 생성된다.
마찬가지로 두 번째 비트의 chip들을 더해보면 -4, 즉 음수로 0이라는 bit가 생성된다.
이렇게 디멀티플렉서는 스테이션 A에서 비트스트림 {1, 0}을 전송받은 것이다.
Statistical Multiplexing: 통계적 다중화
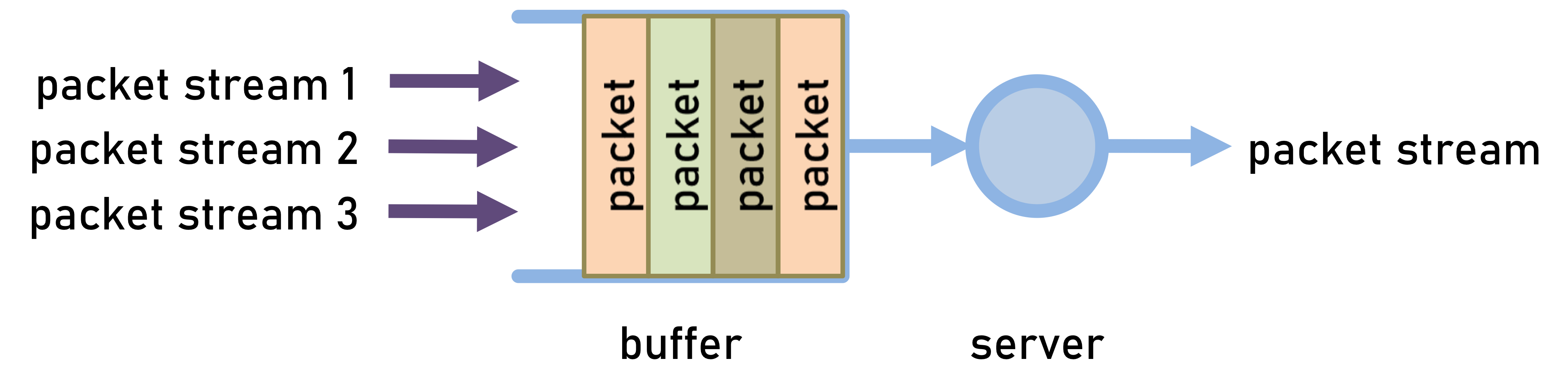
통계적 다중화기는 단일 서버와 단일 버퍼로 구성된 Queueing(대기) 시스템이다.
여러 개의 패킷스트림이 큐잉 시스템에 도착하고, 도착한 패킷은 큐의 하단에 저장된다.
서버는 도착한 패킷의 순서에 따라 차례로 처리하는 FCFS(First Come First Served) 규칙을 따른다.
Asynchronous Transfer Mode(ATM) Switch 가 대표적인 예시이다.
시간은 슬롯(slot)으로 이루어져 있고, 모든 패킷의 길이는 고정되어있다. 또한, 패킷을 서빙하는 시간도 일정하다.
- 네트워크에서 Switch란, 네트워크 내의 장치를 연결하고 해당 장치와 데이터 패킷을 주고받는 것이다. 스위치는 여러 장치가 아닌 의도된 단일 장치로만 데이터를 전송한다.
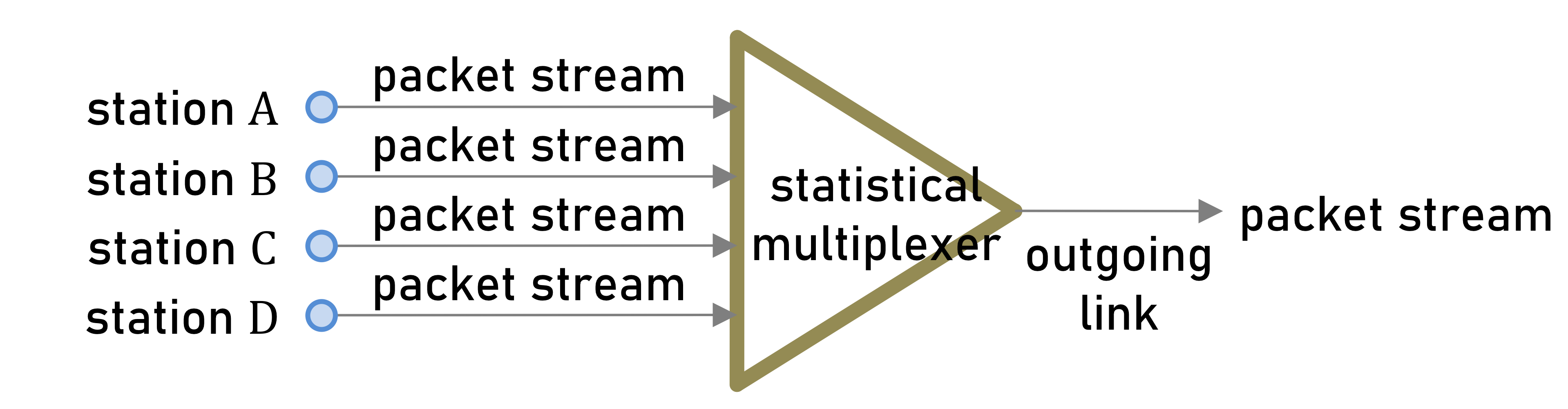
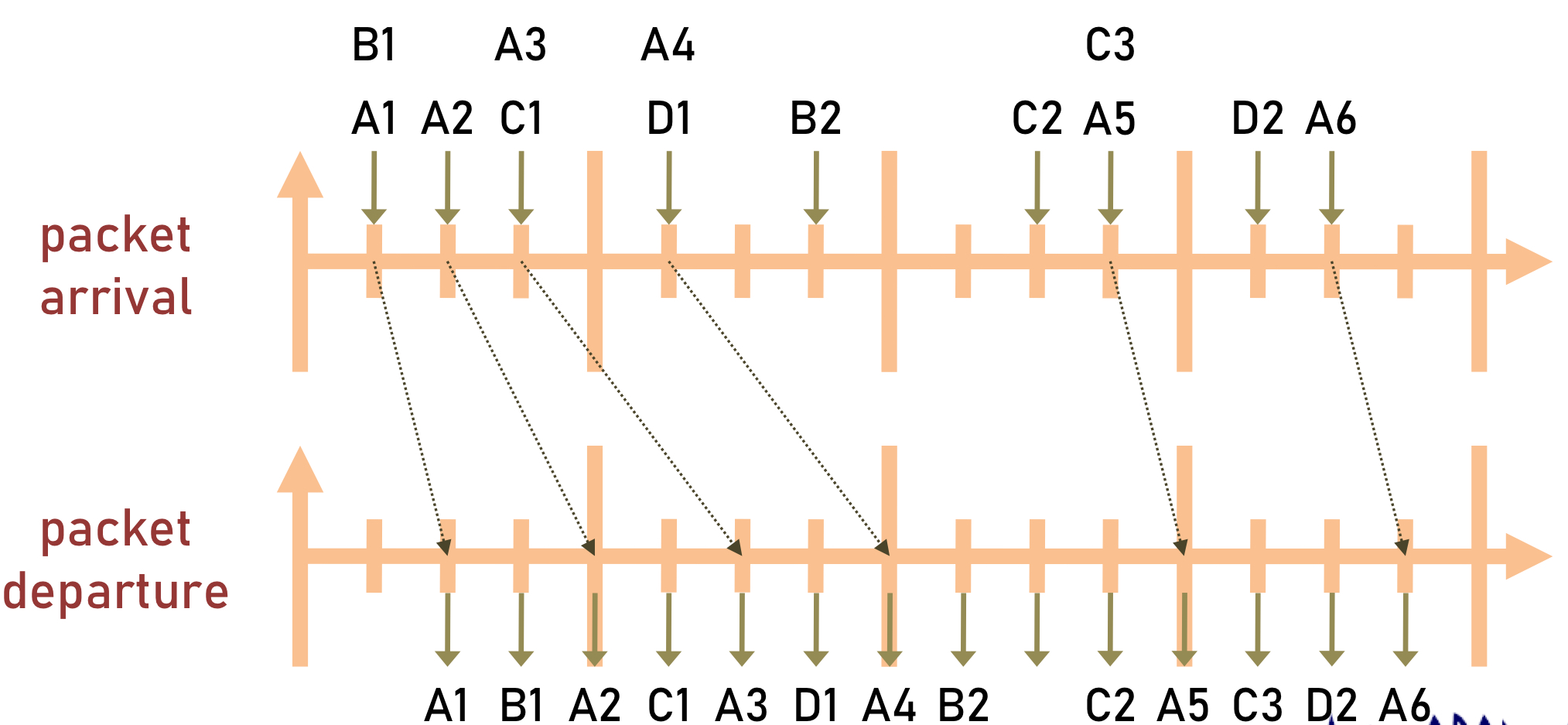
스테이션 A,B,C,D가 전송한 패킷의 도착시간과 이탈시간을 나타낸 그림이다. 각 스테이션은 여러 개의 패킷을 전송할 수 있다.
패킷의 처리하는 시간이 1 slot time이라고 가정한 후에, 패킷 이탈시간을 그렸다.
A1 패킷이 도착하고 처리 시간 1 slot이 지난 후에 A1패킷이 이탈했다.
A1과 거의 동시에 도착했지만 두번째로 도착한 B1은 A1패킷이 이탈한 후, 1 slot이 지난 후에 이탈했다.
이런 식으로 차례로 도착한 패킷들은 처리 시간 1 slot이 지난 후에 큐를 이탈한다.
Time Division Multiplexing: 시분할 다중화
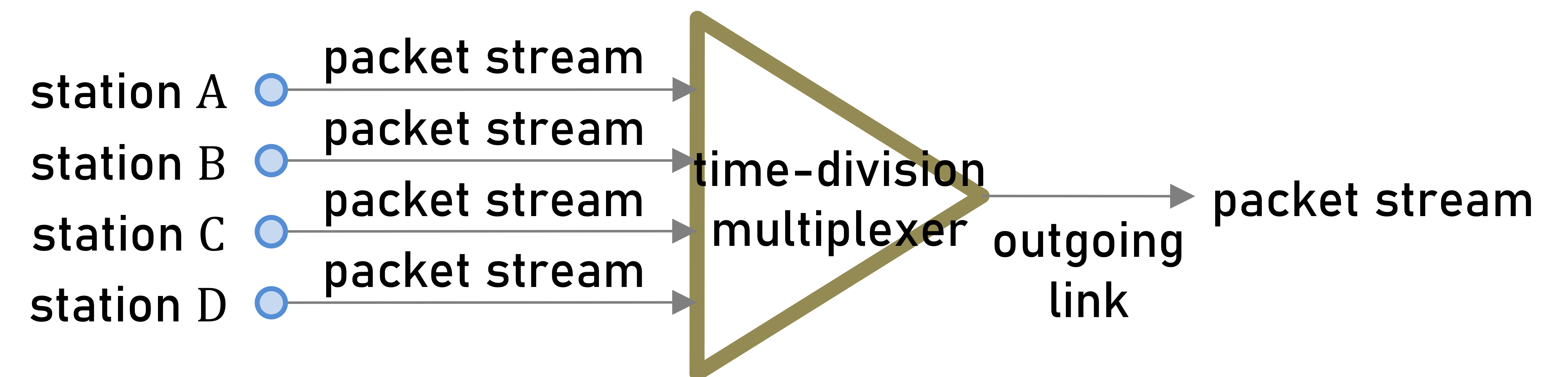
시분할 다중화에서도 역시 송출 링크의 시간은 프레임으로 나눠지며, 각 프레임은 4개의 슬롯으로 분할된다.
각 프레임의 1번째, 2번째, 3번째, 4번째 슬롯을 각각 스테이션 A, B, C, D에 할당한다는 것과, 각 패킷을 처리하는데 걸리는 시간은 1 슬롯이라는 것을 가정한다.
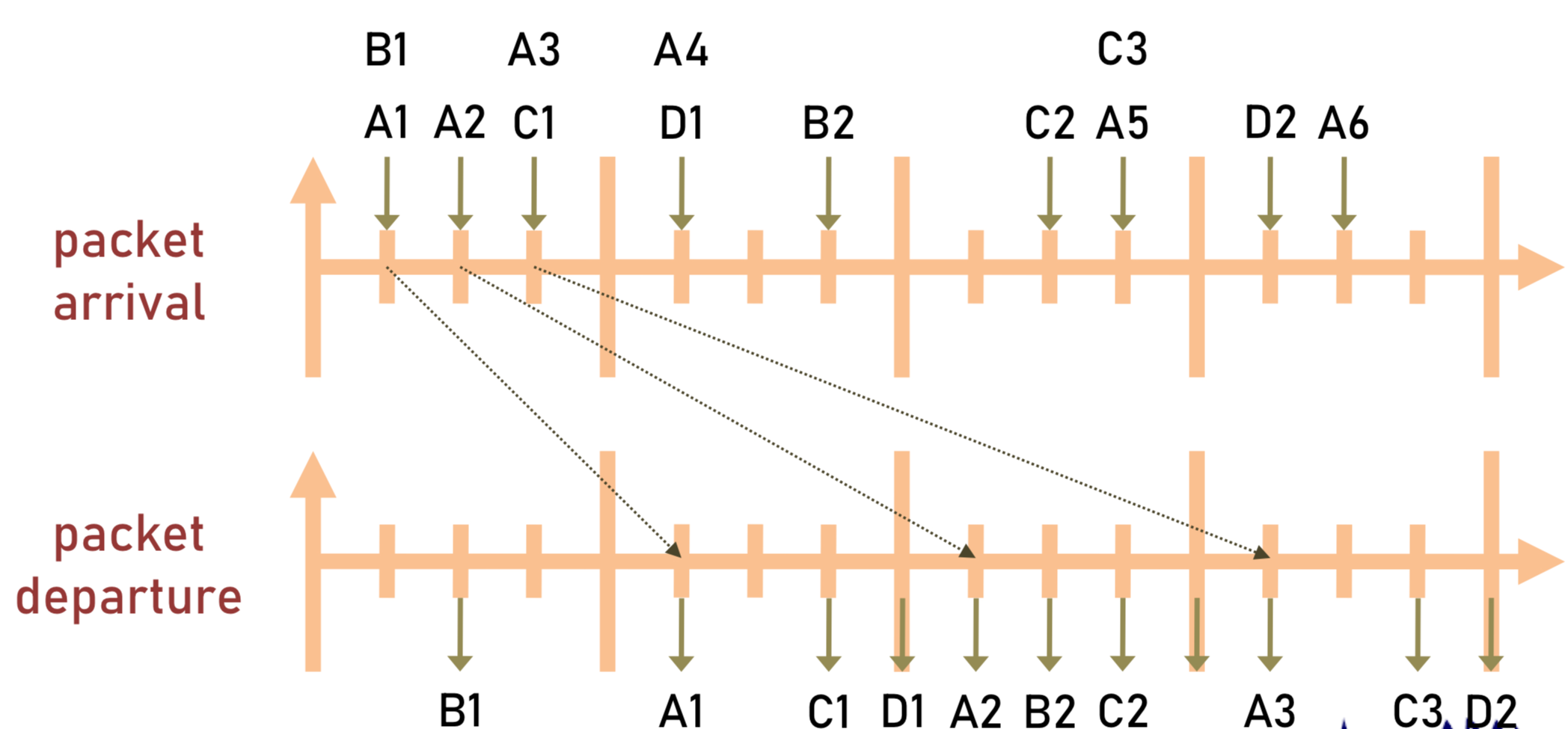
A1이 1번째로 도착했지만, 1번째 프레임의 A칸은 이미 과거라서 사용이 불가능 하기 때문에 2번째 프레임의 1번째 슬롯에 할당되었고, 처리 시간 1슬롯이 지난 후에 이탈하였다.
2번째로 도착한 B1은 A1보다 늦게 도착했지만 운이 좋게(?) 바로 1번째 프레임의 2번째 칸을 할당받게 되었다.
A2는 이미 2번째 프레임의 A칸은 사용했으므로, 3번째 프레임의 A칸에 할당되었다.
Total Throughput의 비교
Statistical Multiplexing 의 처리량
큐잉 시스템을 쉽게 설명하기 위해, 깔때기를 상상해보자.
물이 위에서 계속 흘러들어올 것이고, 깔때기의 파이프를 통해 물이 흘러나갈 것이다.
흘러들어오는 물은 패킷으로, 깔때기에 고여있는 물은 버퍼에서 대기 중인 패킷으로, 흘러나가는 물은 처리된 패킷으로 볼 수 있다.
물이 흘러나가는 속도에 비해 들어오는 속도가 더 높다면, 물은 당연히 깔때기 밖으로 넘칠 것이다. 이렇게 넘치는 물은 한정된 버퍼 사이즈로 인해 소실되는 패킷으로 볼 수 있다.
$\lambda$가 패킷 도착 비율이라고 하고, $\mu$가 패킷 처리 비율이라고 하자.
$\lambda < \mu$라면, 깔때기의 물은 넘치지 않을 것이다. 이러한 상태를 Under bounded state라고 한다.
$\lambda \geq \mu$라면, 깔때기의 물은 넘칠 것이다. 이러한 상태를 Over bounded state라고 한다.
$\eta$가 총 처리량이라면, Under bounded state일 때는 $\eta = \lambda$일 것이고, Over bounded state일 때는 $\eta = \mu$이다.
그렇다면 각 유저(m)의 처리량은 어떻게 되는 것일까?
under bounded state일 때는 패킷이 도착한 대로 처리될 것이니 $\eta^{(m)} = \lambda^{(m)}$이 된다.
문제는 over bounded state일 때다. 유실된 패킷이 존재할텐데, 유저의 처리량은 어떻게 변할까?
답은 '각 유저들의 패킷 처리 비율은 동일하다' 이다.

물론 소실되는 패킷이 존재하기 때문에 절대량은 다를테지만, 처리되는 비율은 패킷 도착 비율이랑 동일하다.
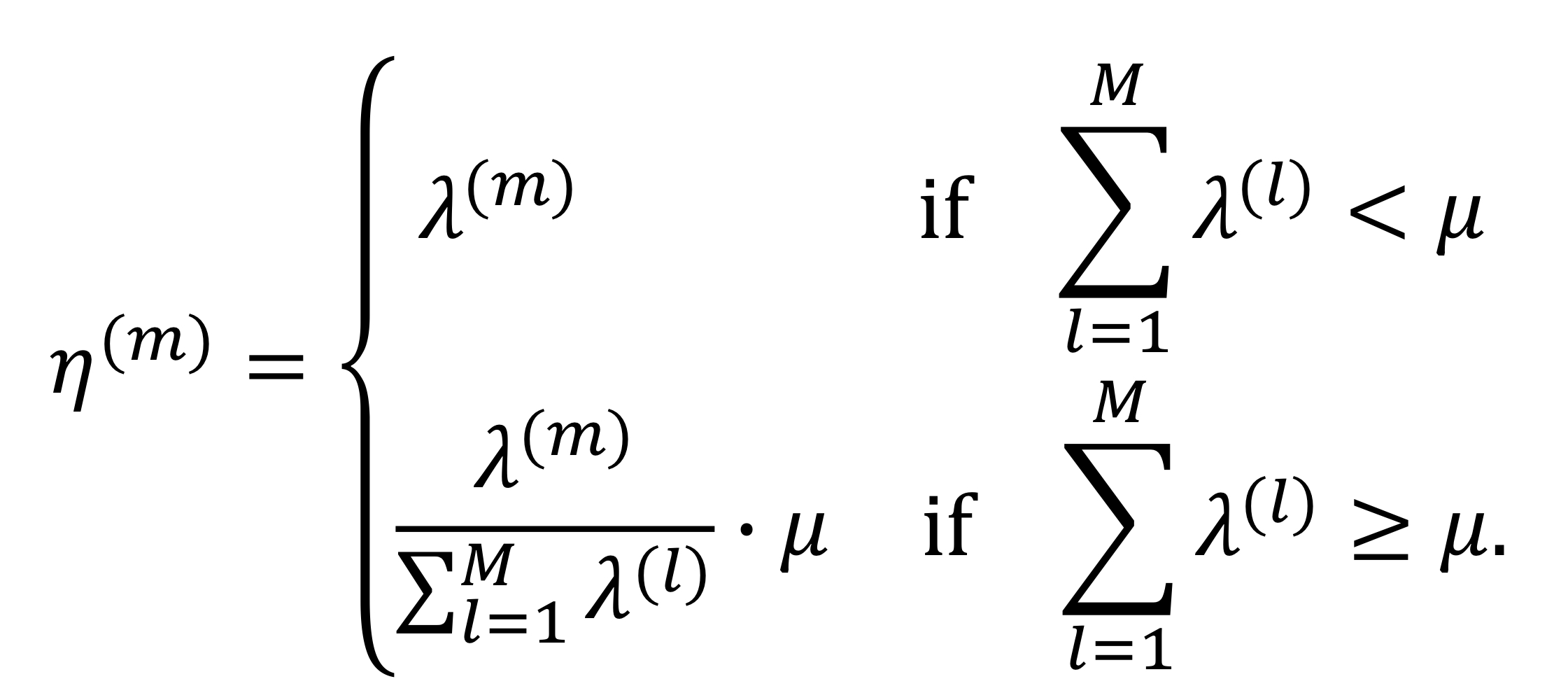
결국, over bounded state의 유저 처리량은 '(계산하려는 유저의 패킷/모든 유저의 패킷) × 처리비율' 이 된다.
TDM의 처리량
TDM은 한 슬롯에 한 스테이션을 할당한다. 나에게 할당된 한 슬롯은 오로지 나만이 사용 가능하다.
이 말을 깔때기로 비유해보자면, 각 유저마다 깔때기를 가지고 있는 것이다.
뭐야 더 좋잖아? 라고 생각할 수도 있지만, 깔때기의 파이프 크기는 유저 수에 반비례할 것이다.
4명의 유저가 있다면, 각각의 깔때기 통로의 크기는 $\frac{\mu}{4}$가 되는 것이다.
그렇다면 TDM의 각 유저 처리량은 어떻게 될까.
한 유저의 도착 패킷 비율이 처리 패킷 비율보다 작다면, $\lambda^{(m)}$가 될 것이다.
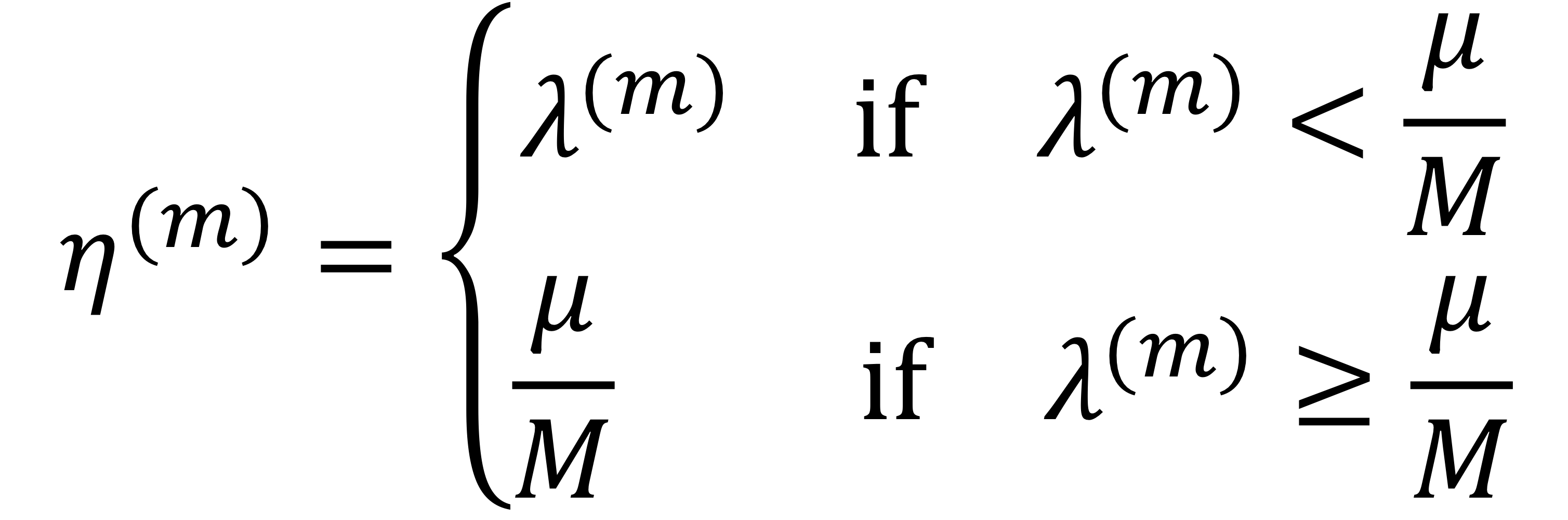
도착 패킷 비율이 더 크더라도, 유저들마다 깔때기를 가지고 있기 때문에 최대로 처리해봤자 깔때기 통로 크기를 벗어나지 못한다.
확실히 계산은 Statistical보다 간편하다.
그러면 Statistical과 TDM 중, 어느 멀티플렉서의 처리량이 더 높은 것일까?
첫 번째 가정이다.
$\mu = 10$이고,
$\lambda_1 = 5, \lambda_2 = 1, \lambda_3 = 1, \lambda_4 = 2$라고 해보자.
모든 유저의 도착 패킷이 처리 패킷 비율을 넘지 않는다.

Statistical의 총 처리량은 9, TDM의 총 처리량은 26/4이다.
TDM의 총 처리량이 더 낮다.
두 번째 가정이다.
$\mu = 10$이고,
$\lambda_1 = 12, \lambda_2 = 1, \lambda_3 = 1, \lambda_4 = 2$라고 해보자.
모든 유저의 도착 패킷이 패킷 처리 비율보다 높다.
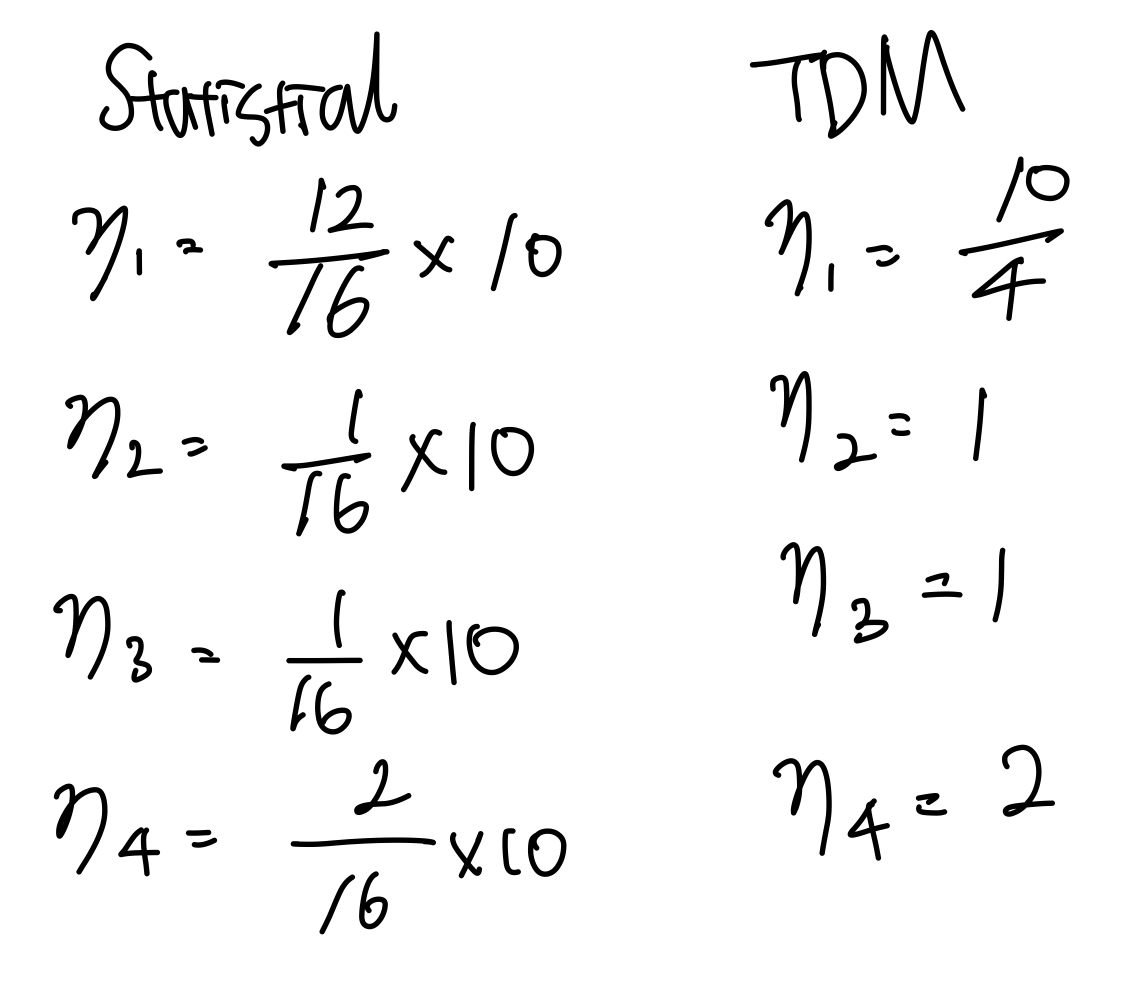
Statistical의 총 처리량은 10, TDM의 총 처리량은 26/4이다.
역시 TDM의 총 처리량이 더 낮다.
처리량이 높은 Statistical이 무조건 더 좋은걸까?
물론, 서비스를 제공하는 입장에서는 총 처리량이 높은 Statistical을 더 선호한다.
하지만 유저 입장에서는 공정성을 따져봐야한다.
Statistical에서는 한 유저가 작은 수의 패킷을 전송하더라도, 많은 패킷을 전송한 유저로 인해 패킷의 손실이 일어나기 때문이다.
각 유저의 패킷 처리량의 공정성에 대해서는 TDM을 더 선호할 수도 있다.
- SAMENESS: 공정성은 모든 것이 평등할 때 생겨난다는 입장이다. 위에서 말한 것처럼 적은 수의 패킷을 보낸 유저가 피해를 받는다면, 그것은 공정하지 않은 것이다. 따라서 SAMENESS를 강조하는 입장의 유저는 TDM을 더 선호한다.
- DESERVEDNESS: 유저가 많이 일하면 많이 일한만큼 받고, 적게 일하면 적게 일한만큼 받아야한다는 입장이다. 도착 패킷 비율과 처리량 비율이 똑같은 Statistical이 이에 해당한다.
- NEED: 필요에 따라 공평하게 나누는 입장이다. Max-Min fair share algorithm이 이에 해당한다. 각 유저가 처리 비용을 공정하게 나눠 가진 후, 패킷을 처리한다. 만약 유저A가 패킷을 처리하고 비용이 남았다고 하자. 그러면 그 비용을 비용이 부족한 유저들에게 공정하게 나눠주는 방식이다. 패킷 처리 비용을 다 쓸 때까지 이를 반복한다.
Delay
딜레이를 볼때는 위의 프레임 사진을 다시 봐야한다.
$A_k$는 도착 시간, $R_k$는 처리 시간으로 봤을 때, $R_k - A_k$의 값이 딜레이가 된다.
물론 딜레이가 더 짧게 걸리는 경우가 성능이 높다고 본다.
** 대학교 수업을 듣고 이해한 부분을 최대한 풀어서 작성한 글입니다.
틀린 정보가 존재할 수 있으며, 언제나 피드백은 환영입니다. **
'DKU > 데이터 통신' 카테고리의 다른 글
| Multiple Access 2 (0) | 2024.10.22 |
|---|---|
| Multiple Access (0) | 2024.10.16 |
| Multiplexing (4) | 2024.09.30 |
| Packet (1) | 2024.09.03 |
| Frequency (0) | 2024.09.03 |