전 글에서는 Stop and Wait ARQ에 대해서 배웠다.
이번 글에서는 Go Back N ARQ에 대해 알아볼 것이다.
Go Back N ARQ
먼저 Go Back N ARQ 에서 송신자와 수신자가 어떻게 작동하는지 알아보자.
대기열의 맨 앞에 패킷이 있고, 전송할 준비가 되었다면 해당 패킷을 전송한다.
ACK timer를 시작하고 대기열의 후속 패킷을 전송한다. 전송되었지만 아직 확인되지 않은 패킷 수가 N을 초과하지 않는 한 계속 전송이 가능하다.
타임 아웃 기간 내에 ACK를 수신했는지 확인한다. 수신했다면, 대기열의 맨 앞에 있는 패킷을 제거하고, 새로운 대기열의 맨 앞 패킷에 대한 ACK 타이머를 갱신한다. 이때도 역시 대기열의 후속 패킷을 전송하되, 전송되었지만 아직 확인되지 않은 패킷 수가 N을 초과하지 않는 한 계속 전송이 가능하다. 만약 수신하지 못했다면, 대기열의 맨 앞에 있는 패킷을 재전송하고, ACK 타이머를 갱신한다. 이때도 역시 후속 패킷의 전송이 가능하다.
글만 읽으면 이해가 어려우니, 예시를 하나 들어보자.

이 예시에서의 파라미터 N은 4로 정해져있다.
패킷 1을 보낸 후에, 후속 패킷 2, 3, 4를 모두 전송하는 것이 보인다. 하지만 1에 대한 ACK을 받지 못했기 때문에, 타임 아웃 기간이 끝나고 1을 재전송했다. 1이 성공적으로 수신된 후에는 패킷 2의 ACK을 받지 못해 2를 재전송 했다. 패킷 2를 재전송할 때의 타임 아웃 기간이 갱신되는 것(빨간 줄)을 볼 수 있다.
$S^{(k)}$의 기간 동안에, 수신자는 k번째 패킷을 에러없이 수신할 수 있었다.
파라미터 N
매개변수 N은 송신자가 ACK을 받지 않고 연속적으로 전송할 수 있는 최대 패킷 수를 나타내는 설계 매개변수이다.
수신자가 패킷을 오류 없이 수신하는 경우, N의 값이 너무 작게 설정되면 송신자는 추가적인 후속 패킷을 전송할 수 없게 되므로 시간이 낭비된다. 즉, 송신자는 ACK을 기다리느라 대기 시간이 길어지고 전송 효율이 저하된다.
수신자가 오류 있는 패킷을 수신하는 경우, N의 값이 너무 크게 설정되면 송신자는 ACK없이 더 많은 후속 패킷을 전송할 수 있으므로 전력 낭비가 발생할 수 있다. 송신된 패킷이 오류가 있는 경우에도 계속 전송을 진행하기 때문에 불필요한 에너지와 리소스를 소모하게 된다.
최적의 타임아웃기간을 사용한다고 가정한 경우, N의 최적값에 대해 알아보자.
다음 두 가지 조건을 만족할 때, N이 최적이 된다.
- $N^*T_P \leq T_P+T_{TO}$
- $(N^*-1)T_P < T_P + T_{TO}$
그러므로, $N^*$ = min{$N \in N: NT_P \leq T_P + T_{TO}$} 이 된다.
이는 아래와 같은 식으로 표현될 수 있다.


위 그림은 파라미터 N이 4로 정해져있는 그림이다. 그림을 보면, 4의 값은 너무 작다는 것을 알 수 있다.
수신자가 에러가 없는 패킷을 받는 경우, 4개의 패킷을 모두 전송하고도 ACK을 받기까지의 시간이 남는다.
수신자가 에러가 있는 패킷을 받는 경우, 재전송을 하기 위해 타임아웃 기간이 끝날 때까지 기다려야한다.

위 그림은 파라미터 N이 10으로 정해져있는 그림이다. 그림을 보면, 10의 값은 너무 크다는 것을 알 수 있다.
수신자가 에러가 없는 패킷을 받는 경우, ACK이 없어도 너무 많은 패킷을 전송하게 되어 필요 이상으로 많은 데이터를 전송할 가능성이 있다.
수신자가 에러가 있는 패킷을 받는 경우, ACK이 없어도 너무 많은 패킷을 전송하고, 해당 패킷 이후의 모든 패킷은 무효가 되어버린다.
최적의 N값을 구하는 예시를 들어보겠다.
$T_{ACK} = T_P$이고, $T_{PRO}=2.8T_P$ 라고 가정해보자.
또한 최적의 타임 아웃 기간이 $T_{TO} = 6.6T_P$라고 가정한다.
그러면, $N^*T_P \leq 7.6T_P$가 되고, $(N^* -1)T_P < 7.6T_P$가 된다.
그러므로 N의 최적의 값은 8이라고 할 수 있다.

N이 최적의 값을 가지고 있을 때의 경우를 분석해보자.
에러가 없는 패킷1을 수신할 것이고, 수신자는 즉시 패킷 1에 대한 ACK을 전송할 것이다. 이 ACK이 송신자에게 도착하는 시간은 6.6$T_P$에서 7.6$T_P$사이이다.
이 경우에는 필요 이상으로 많은 데이터를 전송하지 않게 되고, 이후의 패킷이 무효가 되는 경우도 없다.
Performance
성능 분석을 위해 사용되는 모든 조건은 Stop and Wait ARQ에서 사용된 것과 같다.
송신기의 큐잉 모델 분석부터 조금 달라진다.
- $F_k$는 k번째 패킷의 첫 번째 전송이 시작되는 순간을 나타낸다.
- $L_k$는 k번째 패킷의 마지막 전송이 끝나는 순간을 나타낸다.
$S_k$를 정의하면, $S_k = L_k - max{F_k, L_{k-1}}$이 된다.
$S_k$는 k번째 패킷이 버퍼에서 가장 오래된 패킷으로서 머무르는 체류 시간을 나타낸다.
구체적으로는, $L_k$에서 $L_{k-1}$을 뺀 값이 $S_k$라고 할 수 있다.
또한, k번째 패킷의 체류시간은 다음과 같이 표현될 수 있다.

따라서 $S^{(k)}$의 정규화된 값은 다음과 같이 계산된다.

이제 처리량을 구해보자.
$N_t$는 시간 구간 (0, t] 동안 수신자가 수신한 오류 없는 패킷 수를 나타낸다.
따라서 처리량은 다음과 같이 정의된다. 이는 단위 시간 당 오류 없는 패킷 수로 측정된다.

송신기가 항상 전송할 패킷을 보유하고 있는 포화 상태에서 수신자는 각 패킷의 체류 시간 동안 단 하나의 오류 없는 패킷을 수신한다.
따라서, 포화 상태의 처리량은 다음과 같이 표현된다.

포화 상태의 처리량을 $E(S^{(k)})$를 사용하여 표현하면 다음과 같다.

여기서 만약 송신기가 매개변수 N의 최적 값 $N^*$을 사용할 경우, 포화 상태의 처리량은 다음과 같이 표현된다.
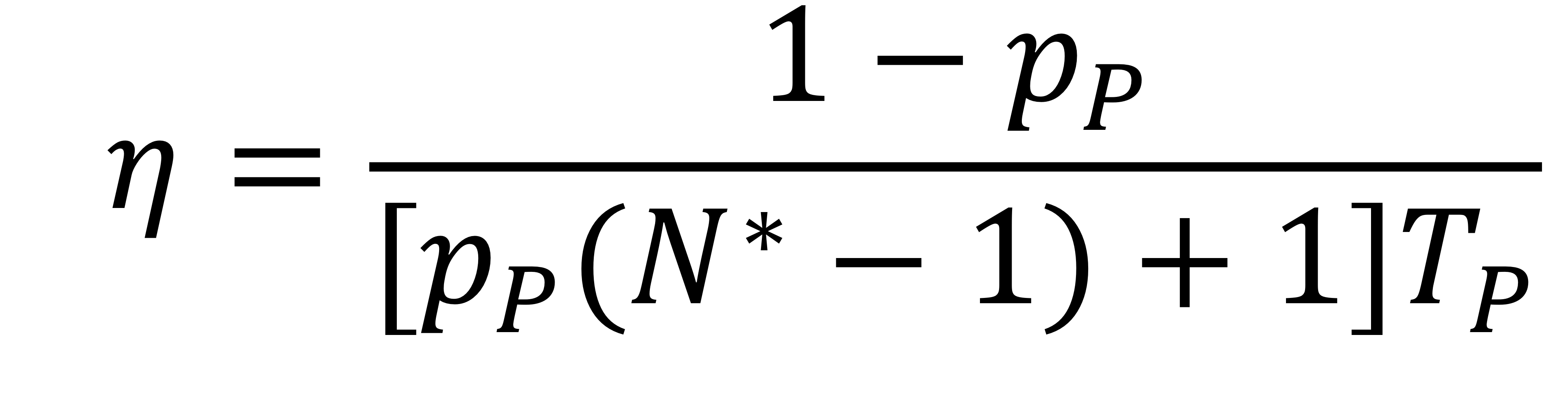
포화 상태의 처리량을 기본 매개변수를 사용할 경우, 포화 상태의 처리량은 다음과 같이 표현된다. (bits/second)

정규화된 포화 상태의 처리량은 비트 전송 시간 당 처리량을 나타내고, 다음과 같이 표현된다.
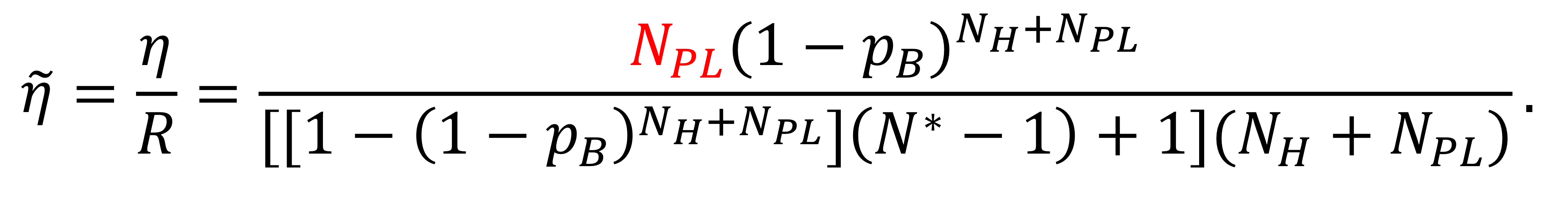
Numerical example: 수치 예상
- 정규화된 포화 상태의 처리량 vs 비트 오류율
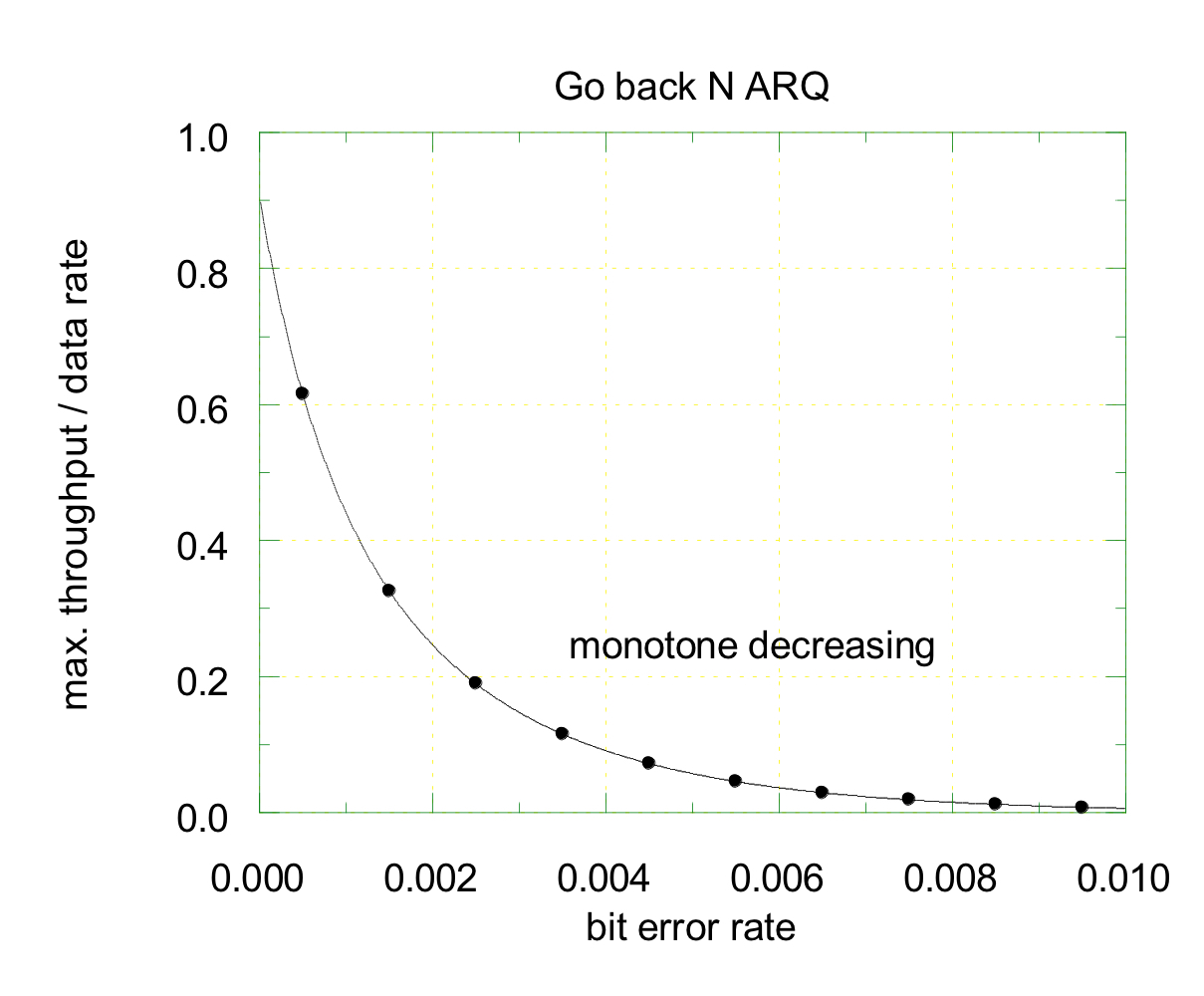
정규화된 포화 상태의 처리량은 비트 오류율이 증가함에 따라 감소한다.
비트 오류율이 증가하면 패킷 내에서 오류가 발생할 확률이 높아지고 처리량이 저하된다. 또한, 비트 오류율이 높아질수록 패킷을 재전송할 필요가 커지기 때문에 효율이 저하된다. 이는 평균 재전송 횟수의 증가로도 이어지고, 네트워크 자원 소모와 전송 지연을 초래한다.
- 정규화된 포화 상태의 처리량 vs 거리
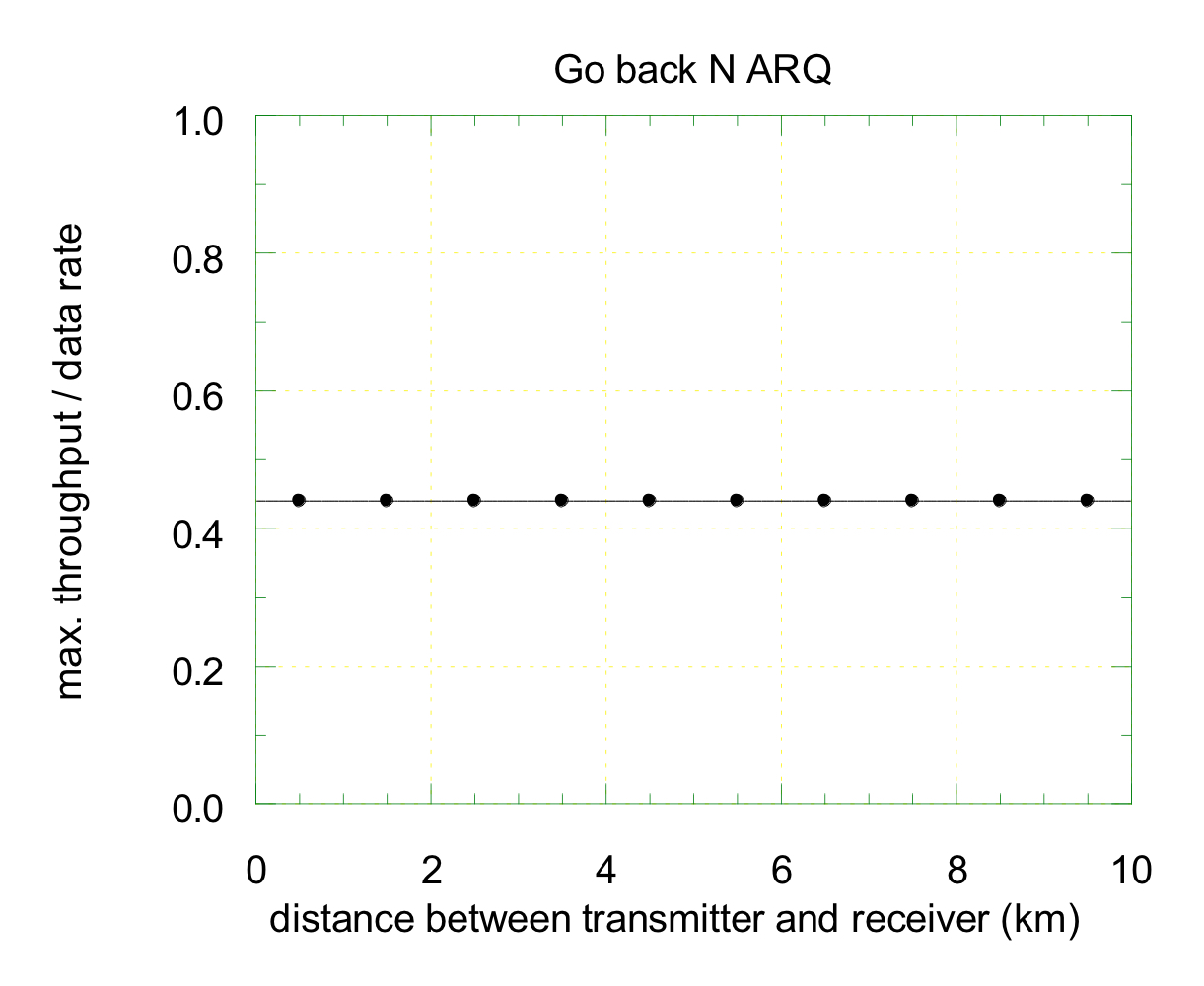
정규화된 포화 상태 처리량은 거리가 증가할수록 감소한다.
피피티 사진은 왜저러는지 모르겠는데.. 일단 설명은 감소한다고 한다.
거리가 증가하면 송신자와 수신자간의 전파 지연 시간이 길어지고, 전체 전송 시간이 늘어나게 된다. 또한 거리가 길어질수록 최적 타임아웃 기간이 증가하고, 송신자는 ACK을 받기 위한 대기 시간이 길어지게 된다.
- 정규화된 포화 상태 처리량 vs 데이터 전송 속도
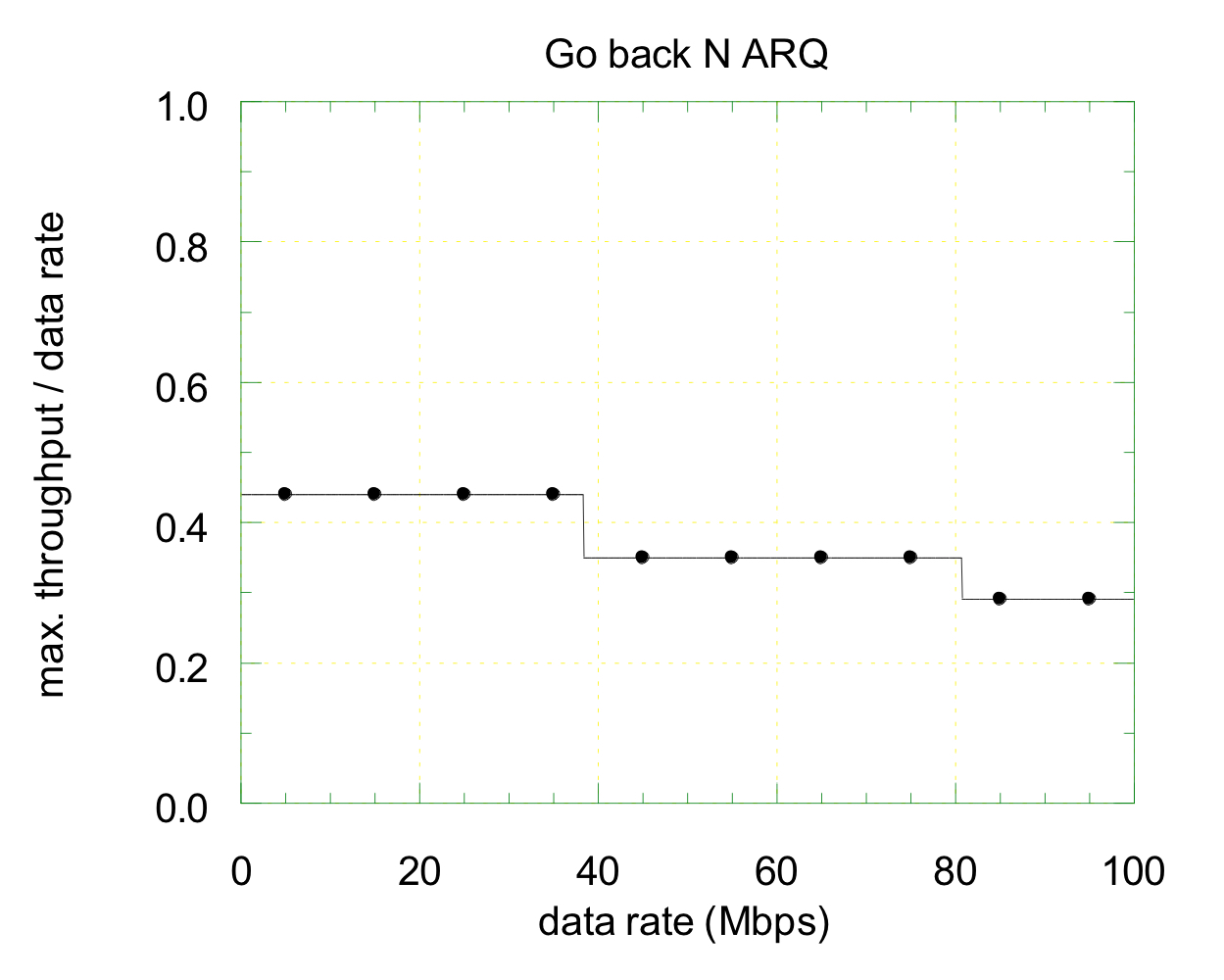
정규화된 포화 상태 처리량은 데이터 전송 속도가 증가함에 따라 감소하는 경향이 있다.
데이터 전송 속도가 높아지면, 송신자는 패킷을 빠르게 전송할 수 있지만 Go back N ARQ에서는 패킷에 대해 ACK을 받아야하므로 대기 시간이 증가한다. 이는 상대적으로 처리량이 감소하게 된다. 또한, 전송 속도가 매우 높아지면 전송 속도에 비해 전파 지연 및 ACK 대기 시간이 상대적으로 커져 처리량이 특정 값에 수렴한다. 결론은, Go back N ARQ는 고속 네트워크에서 비효율적이다.
- 정규화된 포화 상태 처리량 vs 페이로드의 길이
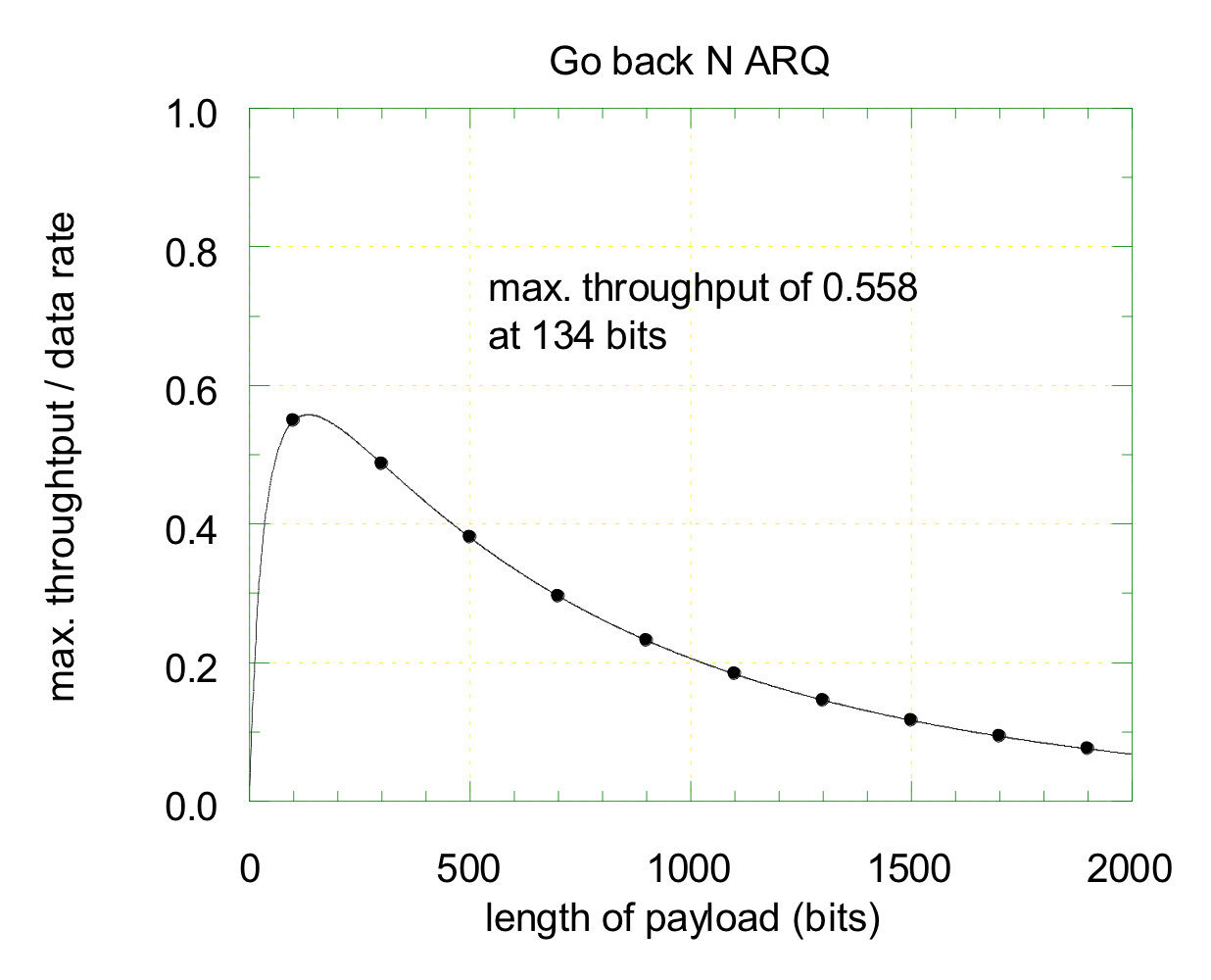
정규화된 포화 상태 처리량을 최소화하는 최적의 페이로드 길이가 존재한다. 즉, 특정 페이로드 길이에서 처리량 효율이 최대화될 수 있다.
사실상 수치 예상 부분도 이전 글에서 배운 내용과 다른 것이 없다. 중복되는 내용은 그냥 넘기도록 하겠다.
복습을 해봤는데, Stop and Wait ARQ와의 차이점을 크게 느끼지 못해서 따로 찾아봤다.
결국 가장 큰 차이점은, Go Back N ARQ는 누적 ACK을 사용한다는 것이다. Stop and Wait ARQ는 각 패킷마다 ACK을 보내는 반면, 누적 ACK은 만약 수신자가 1 ~ 패킷 5까지 정상적으로 수신했다면, 패킷 5에 대한 ACK만을 전송하는 것이다.
즉, 가장 최근에 올바르게 수신된 패킷까지의 ACK만을 송신자에게 보내는 것이다. 패킷 5에서 오류가 발생하면, 패킷 4의 ACK을 보내는 것이다.
아, 그럼 오류가 발생한 패킷을 발견한 후에 그 전 패킷에 대한 ACK을 즉시 보내는 것인가? 라는 생각이 들며 순서가 이상하다는 느낌을 받았다. 정확히 말하자면 그런건 아니고, 패킷 3에서 오류가 발생했다고 할 때, 수신자는 패킷 3 이후의 패킷 4와 5를 버퍼에 저장하지 않고 무시한다고 한다. 결국 버퍼에 저장된 패킷 2에 대한 ACK을 보내는 것이다. 어쨌든 N만큼의 패킷이 계속 전송되긴 하는데, 수신자는 그냥 버퍼에 저장하지 않고 무시하는 거였다.
** 대학교 수업을 듣고 이해한 부분을 최대한 풀어서 작성한 글입니다.
틀린 정보가 존재할 수 있으며, 언제나 피드백은 환영입니다. **
'DKU > 데이터 통신' 카테고리의 다른 글
| Error Control 4 (1) | 2024.11.15 |
|---|---|
| Error Control 3 (0) | 2024.11.14 |
| Error Control (2) | 2024.11.12 |
| Multiple Access 2 (0) | 2024.10.22 |
| Multiple Access (0) | 2024.10.16 |
