Forward Error Correction, FEC (전진 오류 수정)
FEC는 송신자가 패킷에 특수 기능을 추가하여 수신자가 수신된 패킷의 오류를 수정할 수 있도록 한다.
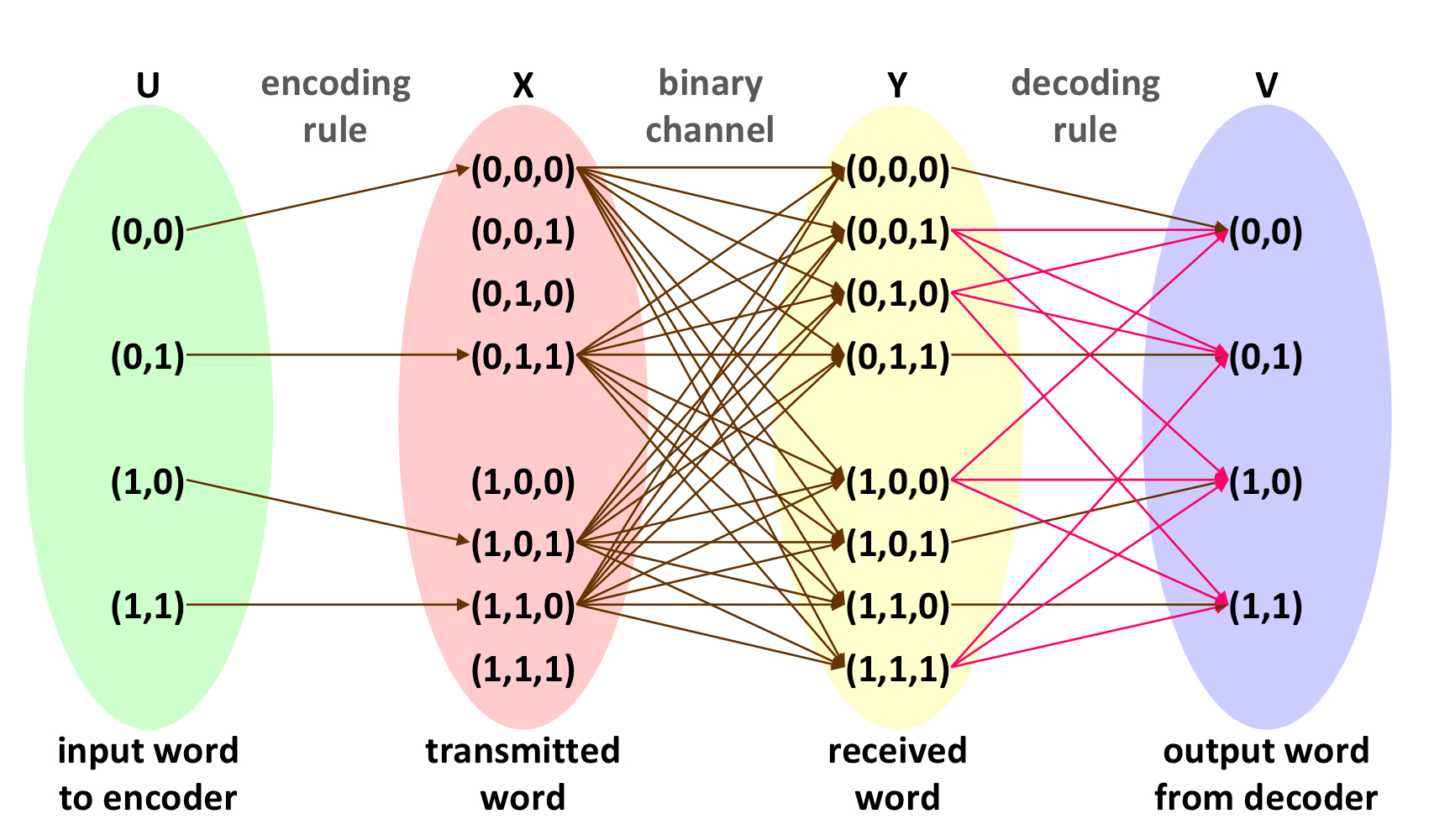
송신기의 인코딩
송신기가 수신기로 전송할 이진 기호 스트림이 있다고 가정한다. 이진 기호 스트림은 길이 k인 기호 블록으로 분할된다.
이러한 기호 블록은 인코더에 입력하는 input word라고 하며, $U = (U_1, ..., U_k)$로 표시된다. 여기서 모든 $i \in \left\{1, ..., k\right\}$에 대해 $U_i \in \left\{1, 0\right\}$ 이다. input word는 $\left\{0, 1\right\}^k$ 집합에서 $2^k$개의 값 중 하나를 가질 수 있다.
인코더는 길이 k인 input word를 인코딩 규칙에 따라 길이 n의 output word로 매핑한다.
일반적으로 $k\leq n$이고, 인코더에서 나오는 output word는 채널을 통해 수신기로 전송된다. 이를 $X = (X_1, ..., X_n)$로 표현하며, 모든 $j \in \left\{1, ..., n\right\}$에 대해 $X_j \in \left\{0, 1\right\}$이다.
길의 n의 단어는 $\left\{0, 1\right\}^n$집합에서 $2^n$개의 값 중 하나를 가질 수 있다. 그러나 인코딩 규칙이 일대일 매칭이기 때문에, output word는 $2^n$개의 값 중 $2^k$개의 고유한 값만 가질 수 있다.
이러한 인코딩 규칙의 범위에 속하는 output word들을 코드워드라고 부른다.
수신기의 디코딩
채널을 통해 전송된 단어 X에 대응하여, 수신기가 단어를 수신했다고 가정한다.
수신된 단어의 길이는 n이며, 이는 디코더에 입력하는 intput word이다. 수신된 단어는 $Y = (Y_1, ..., Y_n)$로 표현되며, 모든 $j \in \left\{1, ..., n\right\}$에 대해 $Y_j \in \left\{0, 1\right\}$이다.
수신기에서 오류 검출을 위한 디코딩
오류 검출을 위한 디코더는 input word Y를 다음 중 하나로 매핑한다. '기호 오류가 검출되었습니다.'와 '기호 오류가 검출되지 않았습니다.' 라는 디코딩 규칙에 따라 오류를 검출한다.
일반적으로, 디코딩 규칙은 input word와 일치하는 코드워드를 찾으려고 한다. 만약 일치하는 코드워드를 찾지 못하면, 디코딩 규칙은 오류가 발생했음을 선언한다. 전송된 단어가 다른 코드워드로 변경된 경우, 이러한 디코딩 규칙은 기호 오류를 검출하지 못할 수도 있다.
수신기에서 오류 수정을 위한 디코딩
오류 수정을 위한 디코딩은 오류 수정 규칙에 따라 코드워드를 선택하고, 해당 코드워드를 디코더에서 생성된 길이 k의 output word로 역매핑한다. 디코더의 output word는 $V = (V_1, ..., V_k)$로 표현되며, 모든 $i \in \left\{1, ..., k\right\}$에 대해 $V_i \in \left\{0, 1\right\}$이다. 수신된 단어 Y가 전송된 단어 X와 같지 않더라도, V = U라면 기호 오류가 수정되었다고 할 수 있다.
다음은 오류 수정에 많이 사용되는 디코딩 규칙들이다.
- Majority Decoding Rule(다수결 디코딩 규칙)
- Maximum Likelihood Decoding Rule (최대 우도 디코딩 규칙)
- Syndrome Decoding Rule (신드롬 디코딩 규칙)

(3, 1) Repitition Code
- Encoding
인코더로의 input word는 $U = (U_1)$이며, $U_1 \in \left\{0, 1\right\}$ 이다.
인코더에서 생성된 output word(채널로 전송되는 단어)는 $X = (X_1, X_2, X_3)$이며, 모든 $j \in \left\{1,2,3\right\}$에 대해 $X_j \in \left\{0,1\right\}$ 이다.
인코딩 규칙은 모든 $j \in \left\{1,2,3,\right\}$에 대해 $X_j = U_1$이다.
그러므로 $C^{(1)} = (0,0,0)$과 $C^{(2)} = (1,1,1)$이라는 코드워드가 생성된다.
즉, (3,1) 반복 코드는 input word가 단일 비트로 구성된 경우 해당 비트를 3번 반복하여 output word를 생성한다.
- Decoding for error detection
디코더로의 input word(채널로부터 수신된 단어)는 $Y = (Y_1, Y_2, Y_3)$이며, 모든 $j \in \left\{1,2,3\right\}$에 대해 $Y_j \in \left\{0,1\right\}$이다.
디코더의 출력은 '단어 오류가 검출되었습니다.' 혹은 '단어 오류가 검출되지 않았습니다.' 로 나뉜다.
오류 검출을 위한 디코딩 규칙으로는 수신된 단어 Y가 어떤 코드워드와도 일치하지 않는 경우, 수신기는 수신된 단어에서 오류가 발생했다고 결정한다. 반대로, 수신된 단어가 코드워드와 일치하면 오류는 발생하지 않았다고 결정한다.
예를 들어, U = (0)이고, X = (0,0,0), Y = (0,0,1)이라면 수신된 단어(Y)가 송신된 코드워드(X)와 다르므로, 수신기는 오류가 발생했다고 결정한다.
다른 예시로, U = (0)이고, X = (0,0,0), Y = (1,1,1)이라면 수신된 단어와 송신된 코드워드가 다르지만, Y는 (1,1,1)이라는 또 다른 코드워드와 일치하게 된다. 따라서 수신기는 오류가 발생하지 않았다고 결정하게 된다.
즉, (3, 1) 반복 코드는 일부 오류를 검출할 수 있으나, 모든 경우에 완벽한 오류 검출을 보장하지 않는다는 것을 알 수 있다.
- Decoding for error correction
디코더에서 생성된 output word는 $V = (V_1)$이며, $V_1 \in \left\{0,1\right\} $이다.
오류 수정을 위한 디코딩 규칙은, Majority Decoding Rule(다수결 디코딩 규칙)을 사용한다.
따라서 0의 개수가 1보다 많으면 V = (0)으로 결정하며, 1의 개수가 0보다 많으면 V = (1)로 결정한다.

(3, 2) Parity Check Code
- Encoding
인코더로의 input word는 $U = (U_1, U_2)$이며, 모든 $i \in \left\{1, 2\right\}$에 대해 $U_i \in \left\{0,1\right\}$이다.
인코더에서 생성된 output word는 $X = (X_1, X_2, X_3)$이며, 모든 $j \in \left\{1,2,3\right\}$에 대해 $X_j \in \left\{0,1\right\}$이다.
인코딩 규칙은 다음과 같다.
- $X_1 = U_1$
- $X_2 = U_2$
- $X_3 = U_1 + U_2 mod 2 = U_1 + U_2$ 이다. 이 값은 모듈로 2 덧셈으로, $U_1$과 $U_2$의 합의 패리티 비트를 나타낸다.
그러므로 4개의 코드워드가 생성된다.
$C^{(1)} = (0,0,0), C^{(2)} = (0,1,1), C^{(3)} = (1,0,1), C^{(4)} = (1,1,0)$
여기서 $X_3$은 Parity symbol로 불린다. 패리티 기호 $X_3$의 값은 전송된 단어가 짝수 패리티를 가지도록 결정된다. 즉, $X_1 + X_2 + X_3 = 0$ 이다.
(3, 2)패리티 검사 코드는 입력된 두 개의 코드를 인코딩 규칙에 따라 인코딩하여 세 개의 비트로 출력한다.
- Decoding for error detection
디코더로의 input word는 $Y = (Y_1, Y_2, Y_3)$이며, 모든 $j \in \left\{1,2,3\right\}$에 대해 $Y_j \in \left\{0,1\right\}$이다.
디코더는 '단어 오류가 검출되었습니다.' 또는 '단어 오류가 검출되지 않았습니다.' 중에 하나를 출력한다.
오류 검출을 위한 디코더 규칙에는 수신된 단어 Y가 홀수 패리티(Y_1 + Y_2 + Y_3 = 1)를 가지면, 수신기는 수신된 단어가에서 오류가 발생했다고 결정한다. 반대로, 짝수 패리티라면 오류가 발생하지 않았다고 결정한다.
예를 들어 U = (0, 0)이고, X = (0, 0, 0), Y = (0, 0, 1)이면 $Y_1 + Y_2 + Y_3 = 1$이다. 따라서 수신기는 홀수 패리티가 발생했다고 판단하여 단어 오류가 발생했다고 결정한다.
- Decoding for error correction
디코더의 output word는 $V = (V_1, V_2)$이며, 모든 $i \in \left\{1,2\right\}$에 대해 $V_i \in \left\{0,1\right\}$이다.
오류 수정을 위한 디코딩 규칙으로 Maximum Likelihood Decoding Rule(최대 우도 디코딩 규칙)을 사용한다.
이는 수신된 단어 Y와 가장 가까운 코드워드 C*을 선택하는 규칙이다.
이때, C* = argmin{$W_H(Y, C_m): m \in \left\{1,2,3,4\right\}$} 으로 정의된다.
여기서 $W_H(A, B)$는 단어 A와 단어 B 사이의 해밍 거리(Hamming distance)이며, 두 단어 간 서로 다른 위치에 있는 비트의 수를 나타낸다. 해밍 거리는 다음과 같이 계산된다. $I${.}는 인디케이터 함수로, 두 비트가 다르면 1, 같으면 0을 반환한다.
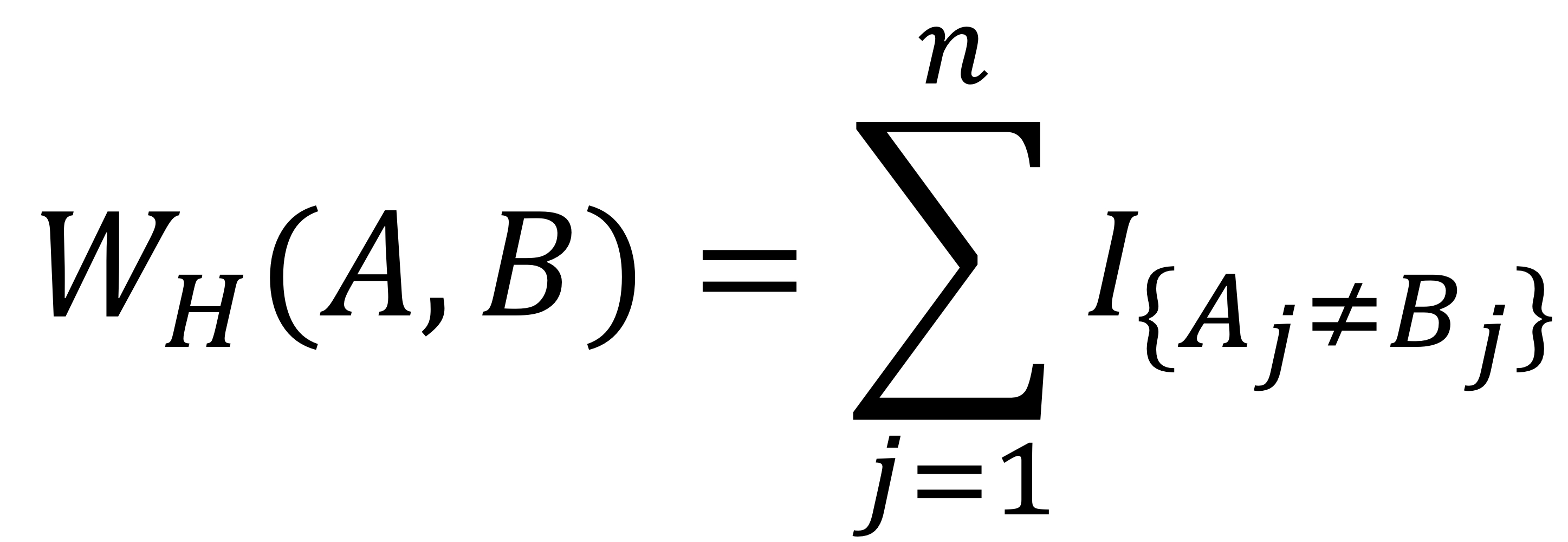
만약 C*가 유일하지 않은 경우, 가능한 여러 코드워드 중 하나를 임의로 선택한다. 그리고 선택한 코드워드 C*을 디코더의 출력 단어 V로 역매핑하여 결과를 찾는다.
만약 symbol error가 발생할 수 있는 확률을 $\epsilon$이라고 한다면, error가 발생하지 않을 확률은 $\epsilon -1$이다.
$P(Y = (0,0,1) | X=(0,0,0))$을 구해보자면, 하나의 단어에서만 오류가 발생했으므로 $(1-\epsilon)(1-\epsilon)\epsilon =(1-\epsilon)^2\epslion$이 된다.
$0 \leq \epsilon < \frac{1}{2}$이므로, 확률을 구해 C*를 선택할 때, 가장 큰 값을 선택하면 된다.
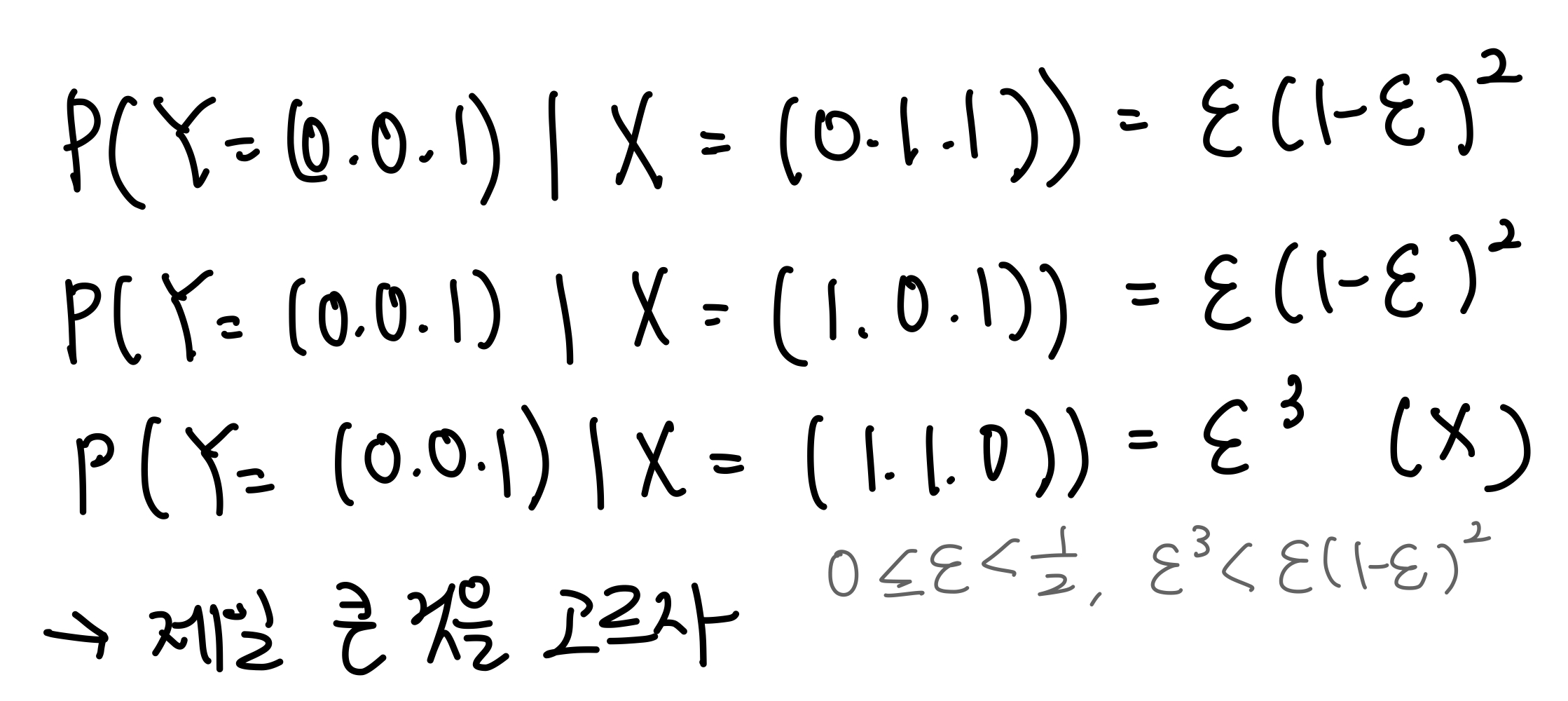
아, FEC부분은 좀 쉽네. 다행이야...
** 대학교 수업을 듣고 이해한 부분을 최대한 풀어서 작성한 글입니다.
틀린 정보가 존재할 수 있으며, 언제나 피드백은 환영입니다. **
'DKU > 데이터 통신' 카테고리의 다른 글
| Error Control 5 (0) | 2024.11.19 |
|---|---|
| ARQ for Deep Space Communications 과제 분석 (2) | 2024.11.16 |
| Error Control 3 (0) | 2024.11.14 |
| Error Control 2 (7) | 2024.11.13 |
| Error Control (2) | 2024.11.12 |
