FEC 이어서
(7, 4) Hamming Code
- Encoding
인코더로의 input word는 $U = (U_1, U_2, U_3, U_4)$이며, 모든 $i \in \left\{1,2,3,4\right\}$에 대해 $U_i \in \left\{0,1\right\}$이다.
인코더에서 생성된 output word는 $X = (X_1, ..., X_7)$이며, 모든 $j \in \left\{1,2,...,7\right\}$에 대해 $X_j \in \left\{0,1\right\}$이다.
인코딩 규칙과 그에 따른 코드워드는 아래와 같다.


- Encoding: 생성행렬
(7, 4) 해밍코드의 생성 행렬(Generator matrix) G는 4×7 행렬로 표현된다.

생성행렬을 통한 인코딩은 $X = UG$로 생성된다.
첫번째 줄을 보면, 1 0 0 0 으로 코드워드를 생성한 것이다.
- Encoding: 패리티 검사 행렬
(7, 4) 해밍코드의 패리티 검사 행렬(Parity check matrix) H는 3×7 행렬로 표현된다.

H는 다음과 같이 구성된다. $H = [P^T|I_3]$
여기서 P는 생성 행렬 G에서 나오는 부분 행렬로, G는 다음과 같이 구성된다. $G = [I_4|P]$
H 역시 첫번째 줄을 보면, 1 1 1 0으로 코드워드를 생성한 것이다.
- Decoding for error correction
디코더로의 input word는 $Y = (Y_1, Y_2, ..., Y_7)$이며, 모든 $j \in \left\{1,...,7\right\}$에 대해 $Y_j \in \left\{0,1\right\}$이다.
디코더의 output word는 $V = (V_1, V_2, V_3, V_4)$이며, 모든 $i \in \left\{1,2,3,4\right\}$에 대해 $V_i \in \left\{0,1\right\}$이다.
오류 수정을 위한 디코딩 규칙으로는 Syndrome decoding rule을 사용한다.
신드롬 S는 다음과 같이 정의된다. $S = YH^T$
따라서 신드롬 S는 다음과 같은 다양한 값을 가질 수 있다.

- : 기호 오류가 발생하지 않았다.
- S =(0,0,1): 7번째 기호에서 오류가 발생했다.
- S =(0,1,0): 6번째 기호에서 오류가 발생했다.
- S =(0,1,1): 4번째 기호에서 오류가 발생했다.
- S =(1,0,0): 5번째 기호에서 오류가 발생했다.
- S =(1,0,1): 1번째 기호에서 오류가 발생했다.
- : 3번째 기호에서 오류가 발생했다.
- : 2번째 기호에서 오류가 발생했다.
예를 들어, U=(1,1,0,1), X=(1,1,0,1,0,0,1), Y=(1,1,0,1,1,0,1)이면 S=(1,0,0)이다. 이는 5번째 기호에서 오류가 발생했음을 나타내고, 수신기는 5번째 기호가 오류임을 결정하고 이를 수정한다. 따라서, 수신된 단어 Y에서 전송된 원래 X로 수정되고 수정된 코드워드로부터 출력된 디코더의 값은 V=(1,1,0,1)이 된다.
하지만, (7, 4)해밍코드가 특정한 경우에 오류 위치를 잘못 판단할 수 있는 가능성도 존재한다.
신드롬 디코딩은 오류 패턴을 사용하는데, 오류패턴은 $E = (E_1, ..., E_7)$ 으로 표현되며, 수신된 단어 Y와 전송된 단어 X의 차이로 정의된다. $E = Y-X=Y+X$
따라서 신드롬 S는 다음과 같이 계산된다. $S = YH^T = (X+E)H^T = XH^T + EH^T $
해밍코드의 특성상 $XH^T =0 $이므로, 신드롬은 다음과 같이 단순화 된다. $S=E・H^T$

- General Hamming Code
(n, k)해밍코드를 고려해보자. G는 k×n 생성 행렬이다. 생성행렬은 $G = [I_k|P]$로 구성되며, 여기서 $P$는 k × (n-k) 행렬이다.
패리티 검사 행렬 $H = [P^T|I_{n-k}]$로 구성되며, $H$는 (n - k) × n 행렬이다.
단일 기호 오류 패턴의 수는 n+1개이고, 신드롬의 수는 $2^{n-k}$개이다. 단일 기호 오류 패턴의 수가 신드롬의 수와 같아야 하므로 $n + 1 = 2^{n-k}$가 된다. 이 관계식은 n-k = d로 가정했을 때, 다음과 같이 변형될 수 있다.
$n = 2^d-1$, $k=2^d-d-1$ (for $d \in (2, 3...)$)
따라서 (3,1), (7,4), (15,11) ... 의 해밍코드가 존재한다.
(n, k) Polynomial Code
- Encoding
인코더로의 input word는 $U = (U_0, U_1, ..., U_{k-1})$이며, 모든 $i \in \left\{0,1...,k-1\right\}$에 대해 $U_i \in \left\{0,1\right\}$이다. input word는 다항식 형식으로 다음과 같이 표현할 수 있다.
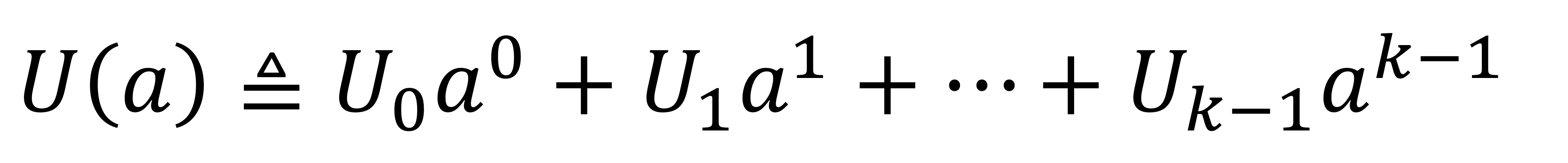
인코더에서 생성된 output word는 $X=(X_0, X_1,...X_{n-1})$이며, 모든 $j \in \left\{0,1,...,n-1\right\}$에 대해 $X_j \in \left\{0,1\right\}$이다. output word는 다항식 형식으로 다음과 같이 표현될 수 있다.
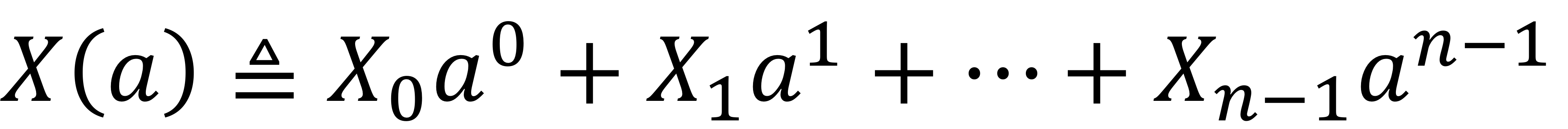
생성기는 $G =(G_0, G_1, ..., G_{n-k})$로 구성되며, 모든 $m \in \left\{0,1,...,n-k\right\}$에 대해 $G_m \in \left\{0,1\right\}$이다. 다항식 형태로는 다음과 같이 표현할 수 있다.
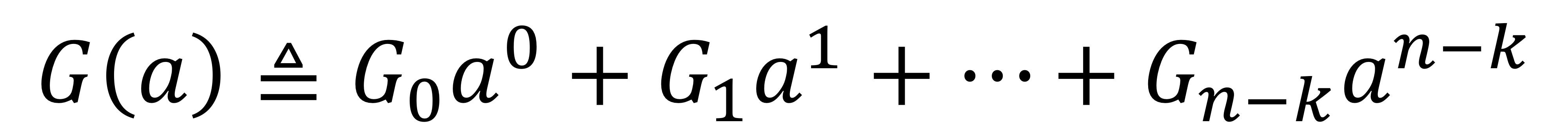
인코딩 규칙은 3단계로 나뉜다.
1단계: 입력 다항식 $U(a)$에 $a^{n-k}$를 곱한다.
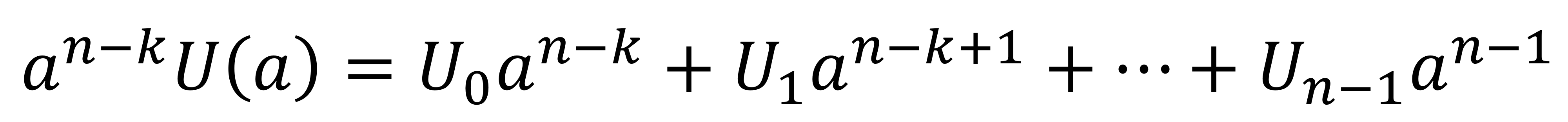
2단계: $a^{n-k}U(a)$를 생성기 다항식 G(a)로 나누어 몫 다항식 Q(a)와 나머지 다항식 R(a)를 얻는다.
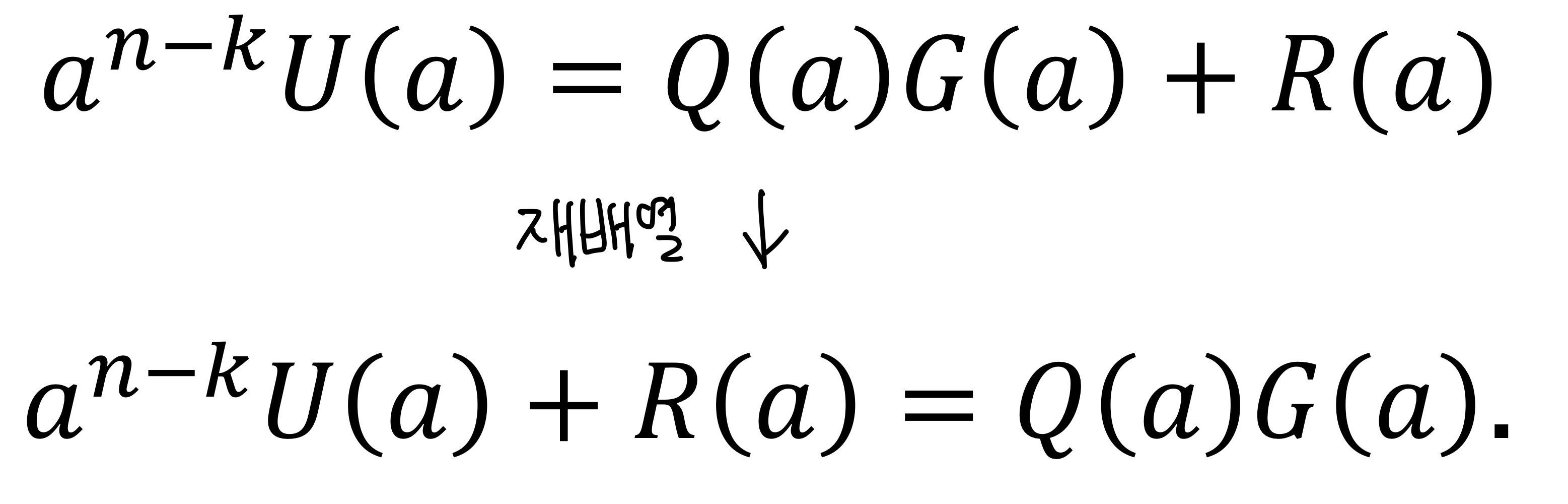
3단계: $a^{n-k}U(a)$에 나머지 R(a)를 더하여 인코딩된 출력 다항식 X(a)를 얻는다.
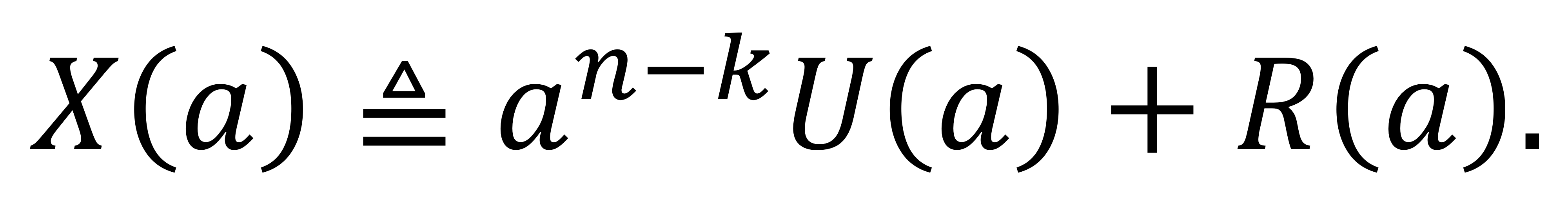
- Decoding for error detection
디코더로의 input word $Y = (Y_0, Y_1, ..., Y_{n-1})$이며, 모든 $j \in \left\{0,1,...,n-1\right\}$에 대해 $Y_j \in \left\{0,1\right\}$이다. 다항식 형태로는 다음과 같이 표현된다.
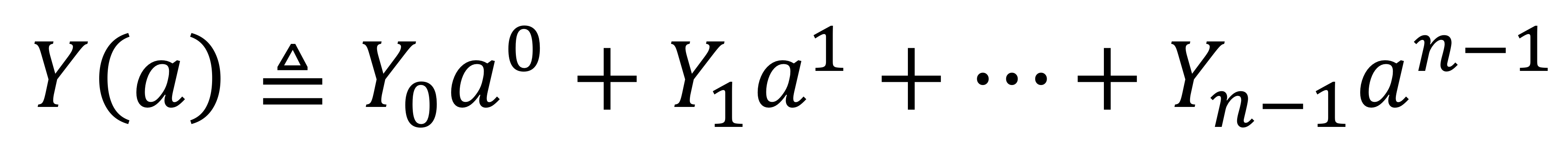
디코딩 규칙은 Q*(a)와 R*(a)를 수신된 다항식 G(a)로 나누어 얻은 몫 다항식과 나머지 다항식이라고 하자.
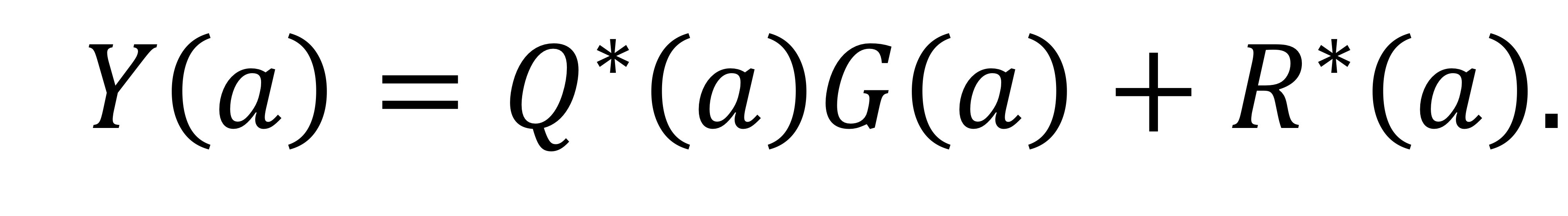
만약 R*(a) = 0이면, 수신기는 단어 오류가 검출되지 않았다고 결정한다. 그렇지 않으면, 수신기는 단어 오류가 검출되었다고 결정한다.
예시를 들어보자.
인코더에 입력된 단어는 U = (0, 1, 0, 1)라고 하자. 입력단어에 대응하는 다항식은 $U(a) = a+a^3$이다.
생성기 다항식은 $G(a) = 1 + a + a^3$이다. 여기서 (7, 4)다항식 코드를 사용한다.
인코딩을 시작한다. 1단계, $a^{n-k}U(a)$를 계산한다. $a^3U(a) = a^4 + a^6$이 된다.
2단계, $a^3U(a) = Q(a)・G(a) + R(a)$에서 Q(a)와 R(a)를 구한다. $Q(a) = 1 + a^3, R(a) = 1+ a$
3단계, 인코더에서 생성된 출력 단어, 즉 채널을 통해 수신기에 전송될 단어는 다음과 같이 계산된다.
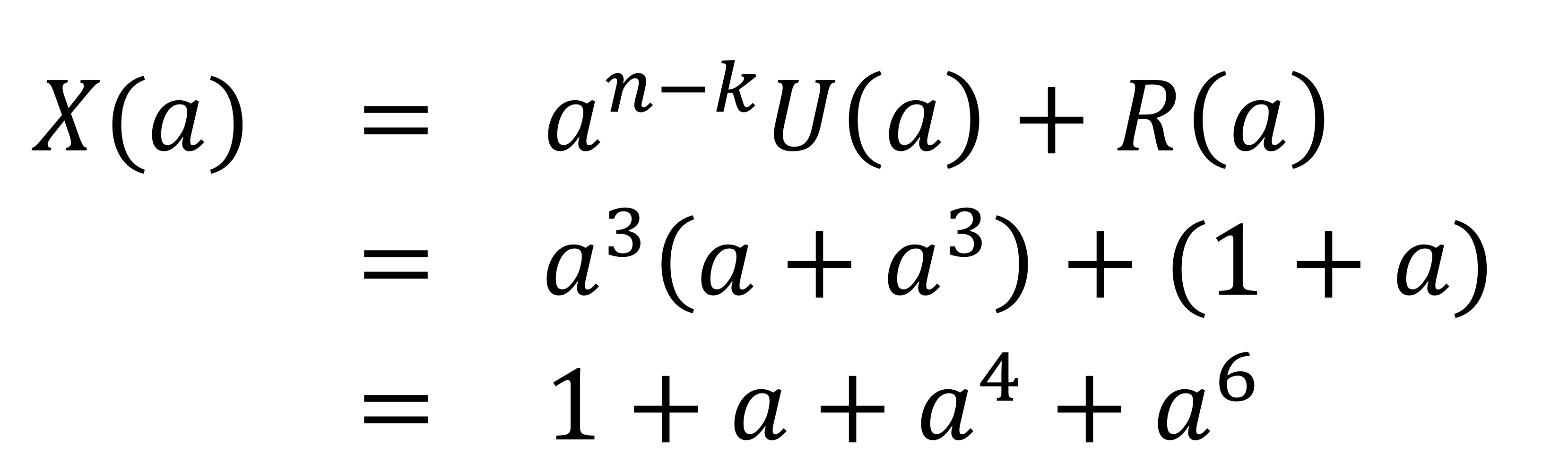
이 다항식은 이진 수열로 (1, 1, 0, 0, 1, 0, 1)에 해당한다.
디코딩을 시작한다. 수신기가 수신한 단어는 Y = (1, 1, 0, 0, 1, 1, 1)이다. 수신된 단어에 대응하는 다항식은 $Y(a) = 1 + a + a^3 + a^4 + a^6$이다. Y(a)를 생성기 다항식 G(a)로 나누어 몫 다항식 Q*(a)와 나머지 다항식 R*(a)를 구한다.
$Y(a) = Q*(a)G(a) + R*(a)$로, 계산하면 $Q*(a) = a^3$이고, $R*(a) = 1+a$이다. R*(a)가 0이 아니므로, 수신기는 단어 오류가 발생했다고 결정한다.
유명한 다항식 코드들은 다음과 같다.
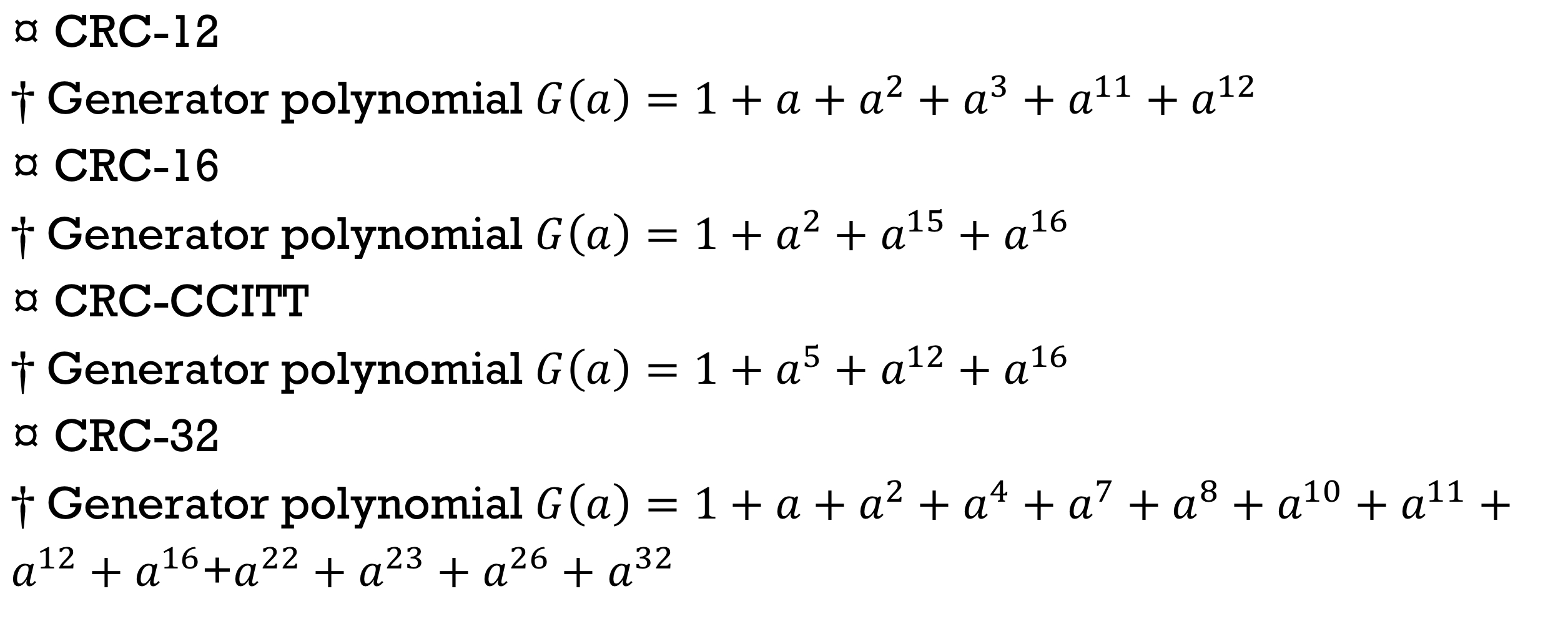
- Error detection capability
수신된 단어에 단일 기호 오류가 발생했다면, G(a)가 두 개 이상의 항을 가지는 경우에는 (n, k)다항식 코드는 항상 이러한 단어 오류를 검출할 수 있다.
수신된 단어에 두 개의 기호 오류가 발생했다면, G(a)가 세 개의 항을 가지는 인자의 경우에는 (n, k)다항식 코드는 항상 이러한 단어 오류를 검출할 수 있다.
수신된 단어에 홀수 개의 기호 오류가 발생했다면, G(a)가 (1+a)라는 인자를 포함하는 경우, (n, k)다항식 코드는 항상 이러한 단어 오류를 검출할 수 있다.
** 대학교 수업을 듣고 이해한 부분을 최대한 풀어서 작성한 글입니다.
틀린 정보가 존재할 수 있으며, 언제나 피드백은 환영입니다. **
'DKU > 데이터 통신' 카테고리의 다른 글
| Flow Control (0) | 2024.11.26 |
|---|---|
| Error Control 6 (0) | 2024.11.20 |
| ARQ for Deep Space Communications 과제 분석 (2) | 2024.11.16 |
| Error Control 4 (1) | 2024.11.15 |
| Error Control 3 (0) | 2024.11.14 |
