Performance of FEC
Channel Model
채널의 모델에는 다양한 종류가 존재한다.



Performance anaylsis of (3, 1) Repetition Code
성능 분석을 위한 환경 가정을 먼저 해보겠다.
각 전송된 기호는 독립적으로 0 또는 1일 가능성이 같고, 기호 오류 확률은 $\epsilon \in [0, 1/2]$이다.
- 코드 되지 않은 경우의 검출 실패 확률
코드 되지 않은 경우는 데이터가 전송될 때 오류 검출 및 수정 코드 없이 전송되는 것이다.
기호 오류 확률 $\epsilon$이 주어졌을 때, 전체 오류가 발생할 확률(전송된 기호가 수신될 때 원래의 값과 달라지는 경우)은 다음과 같다.

P(A) = 0 (정상적인 경우)와 P(B) = $\epsilon$(오류가 발생한 경우)일 때, 단어 오류 확률은 $p_{WE} = P(A) + P(B) = \epsilon$이 된다. 또한 검출 실패 확률은 $p_{DF} = \frac{P(B)}{P(A)+P(B)} = 1 $이 된다.
이는 검출 실패 확률이 100%인 것으로, 수신기가 오류를 감지하거나 수정할 수 없다.
- 코드된 경우의 검출 실패 확률
전체 오류가 발생할 확률은 다음과 같다. 전체 오류란, 검출되는 오류와 검출되지 않는 오류를 합한 것이다.

검출되지 않는 오류가 발생할 확률 P(B)는 다음과 같다.

P(B)를 계산하는 방법은, (0 0 0) 데이터를 전송했지만 (1 1 1)을 수신할 경우와 (1 1 1) 데이터를 전송했지만 (0 0 0)을 수신한 경우를 계산하면 된다.
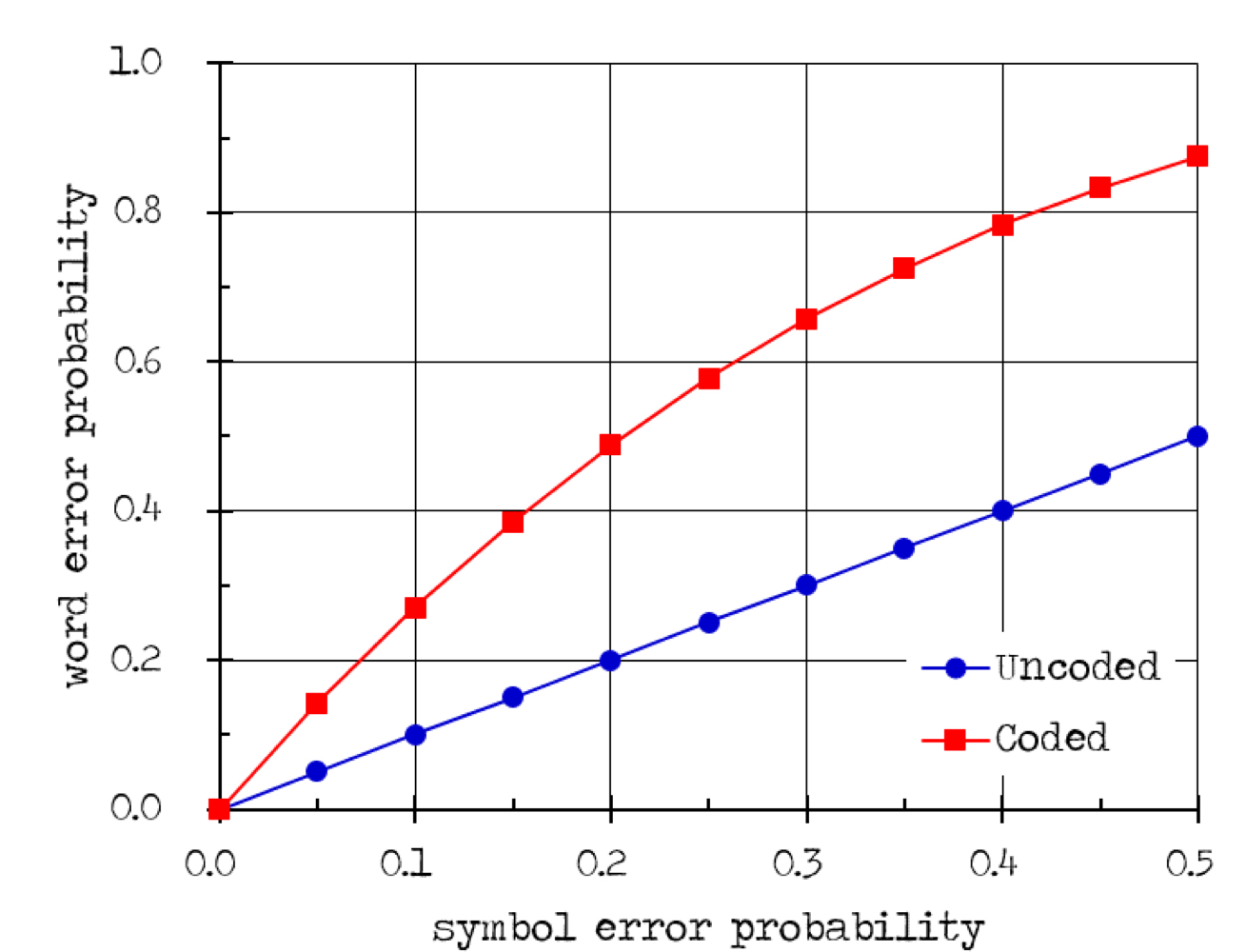
따라서 단어 오류 확률은 다음과 같다.

또한, 검출 오류 확률은 다음과 같다.

- 코드 되지 않은 경우의 수정 실패 확률
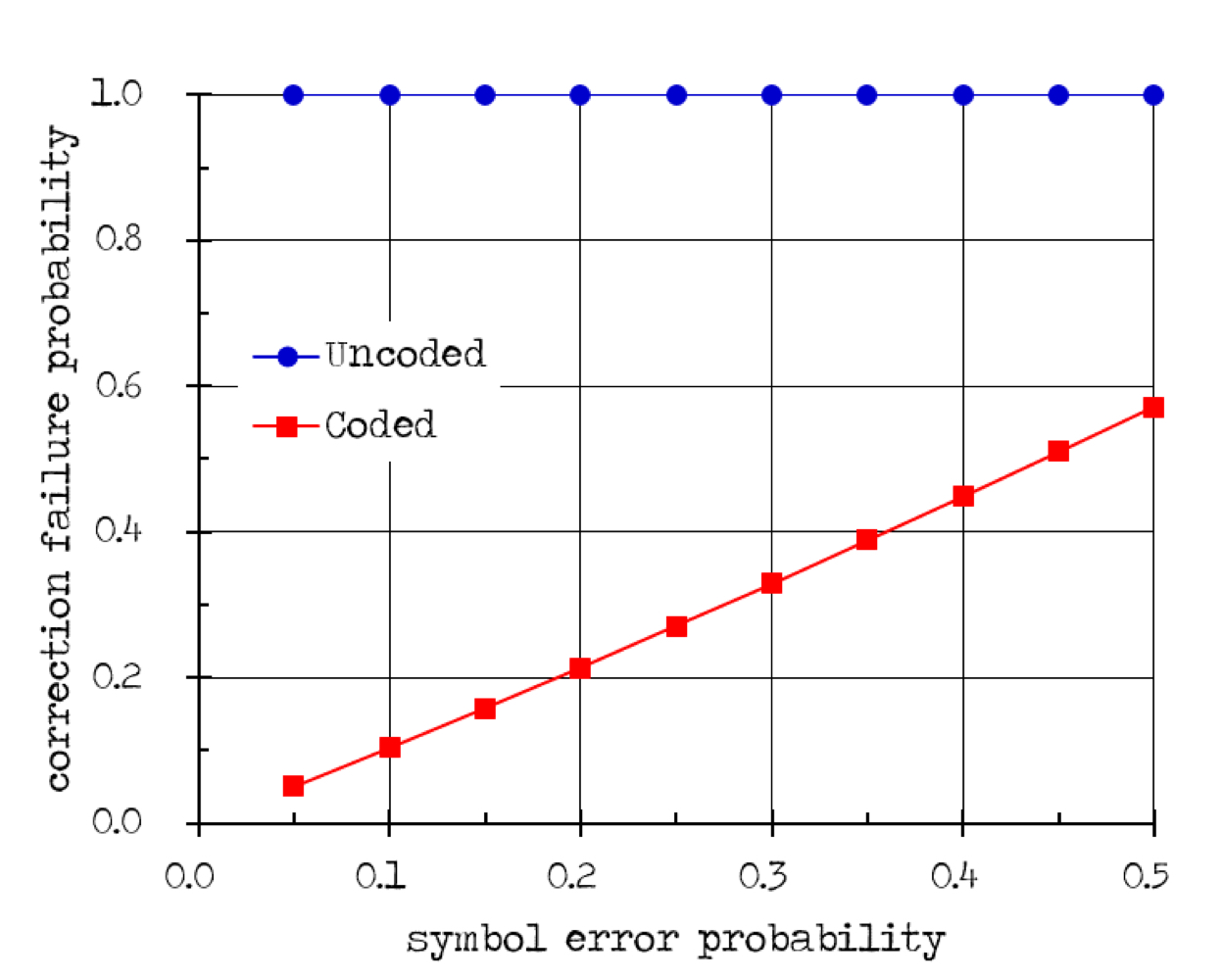
코드 되지 않은 경우의 수정 실패 확률은 코드 되지 않은 경우의 검출 실패확률과 동일하다.
- 코드 된 경우의 수정 실패 확률
P(A)는 수정이 가능할 수 있는 오류 사례고, P(B)는 전송된 데이터가 완전히 잘못 수신된 상태로 남아있는 경우를 의미하고 복구가 불가능하다. P(B)는 전체 오류 확률에서 오류 수정이 가능한 P(A)를 빼서 구한다.

그러므로, 수정 실패 확률은 다음과 같다.

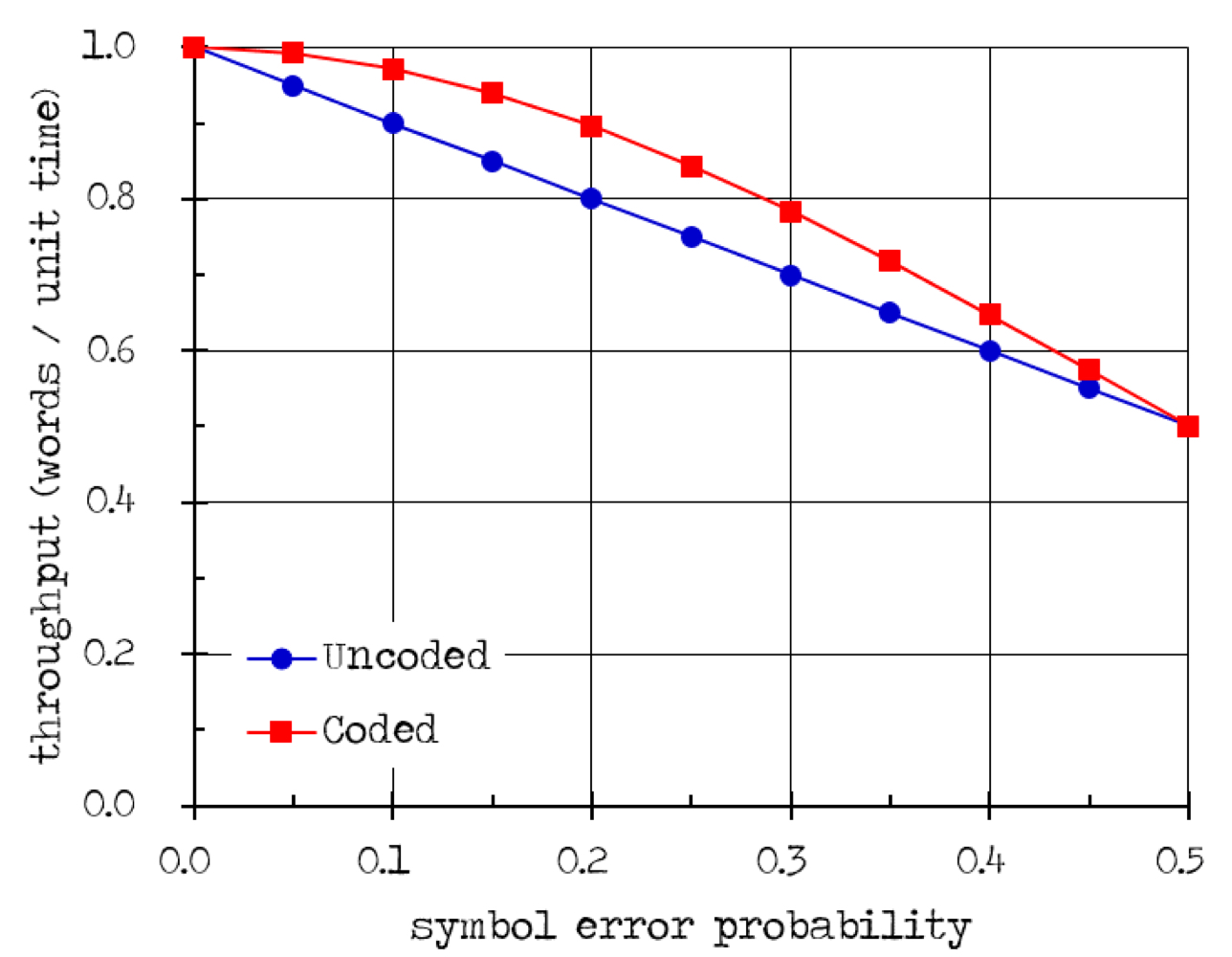
- Throughput
코드되지 않은 경우의 처리량은 다음과 같다.
단위는 words/word transmission time 과 words/symbol transmission time 이다.
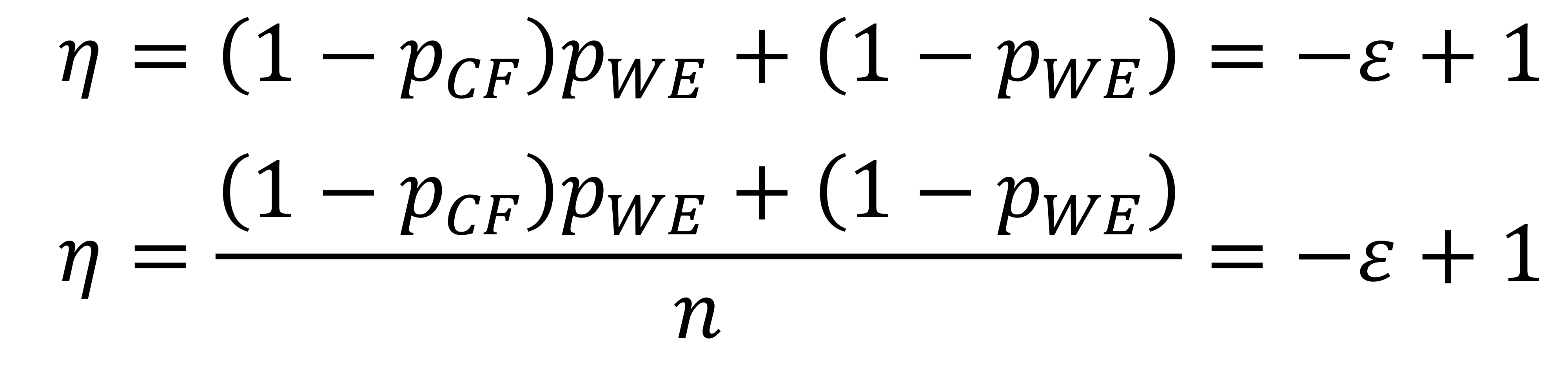
코드된 경우의 처리량은 다음과 같다.
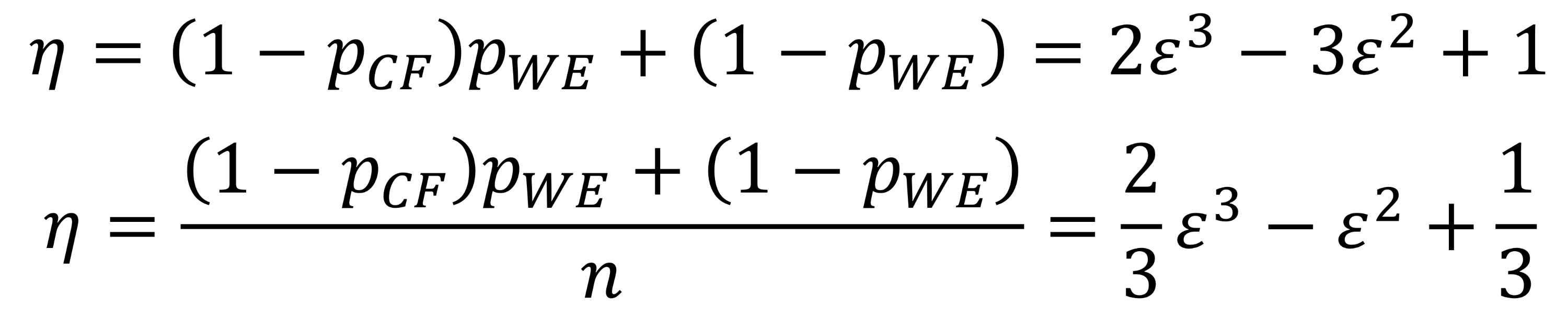
** 대학교 수업을 듣고 이해한 부분을 최대한 풀어서 작성한 글입니다.
틀린 정보가 존재할 수 있으며, 언제나 피드백은 환영입니다. **
'DKU > 데이터 통신' 카테고리의 다른 글
| HDLC(High-level Data Link Protocol) (0) | 2024.12.03 |
|---|---|
| Flow Control (0) | 2024.11.26 |
| Error Control 5 (0) | 2024.11.19 |
| ARQ for Deep Space Communications 과제 분석 (2) | 2024.11.16 |
| Error Control 4 (1) | 2024.11.15 |
