네트워크는 노드 집합과 노드 위에 정의된 방향성 링크 집합으로 이루어진 구조이다.
각 링크에는 실수가 할당된다.
따라서 네트워크 G는 (V, E, A)로 표현된다.
V는 노드들의 집합을, E는 방향성 링크들의 집합을, A는 링크에 할당된 실수의 집합을 나타낸다.

라우팅이란, 네트워크의 출발노드(source node)에서 도착 노드(destination)까지 데이터를 전달하기 위한 경로를 구성하는 과정이다.
경로 결정 위치에 따른 라우팅 방식의 분류
- 각 노드에서 경로 결정을 수행하는 라우팅 방식
- 중앙 노드에서 경로 결정을 수행하는 라우팅 방식
- 시작 노드에서 경로 결정을 수행하는 라우팅 방식
- 일부 노드의 집합에서 경로 결정을 수행하는 라우팅 방식
경로 결정 시점에 따른 라우팅 방식의 분류
- 각 패킷의 전송 시점에 경로 결정을 수행하는 라우팅 방식
- 각 세션의 시작 시점에 경로 결정을 수행하는 라우팅 방식
정보 제공자에 따른 라우팅 방식의 분류
- 정보를 제공받지 않고 경로를 결정하는 라우팅 방식
- 인접 노드들이 제공한 정보를 바탕으로 경로를 결정하는 라우팅 방식
- 로컬 노드가 제공한 정보를 바탕으로 경로를 결정하는 라우팅 방식
- 경로상의 노드들이 제공한 정보를 바탕으로 경로를 결정하는 라우팅 방식
- 모든 노드가 제공한 정보를 바탕으로 경로를 결정하는 라우팅 방식
전략적 요소에 따른 라우팅 방식의 분류
- 정적 라우팅: 각 출발지-목적지 쌍에 대해 미리 지정된 경로를 사용하는 라우팅 방식
- 동적 라우팅: 현재 네트워크의 혼잡 상태에 따라 경로를 결정하는 라우팅 방식
Shortest path routing scheme: 최단 경로 라우팅 방식
네트워크 G = (V, E, A)가 있다. V는 노드들의 집합 {1, ..., n}이며 A는 링크 위에 할당된 값들의 집합 {$a_{ij}: (i, j) \in E$}이다.
$a_{ii}$ =0 이며, i에서 j로 직접 연결된 경로가 없는 경우 $a_{ij}=\infty$이다.
노드 1(시작 노드)에서 모든 다른 노드까지의 최단 경로를 찾는다.
Bellman's equations
출발 노드에서 다른 노드로 가는 최단 거리를 계산하기 위해 다음 방정식을 구성한다.
- $u_1$ = 0
- $u_j$ = min{$u_k + a_{kj}:k \in (1, ..., n)\(j)$}
노드 j로 가는 최단 거리는 j의 직전 노드 k를 통해서 계산되며, k는 j로 직접 연결된 모든 노드들 중에서 선택된다.
최단 경로는 k에서 j까지의 거리 $a_{kj}$와, 노드 1에서 k까지의 최단 거리 $u_k$의 합으로 정의된다. 이 값들 중 최소합을 취한다.
벨만 방정식의 해는 출발 노드에서 다른 모든 노드로 가는 최단 경로의 길이 집합이다.
벨만 방정식이 출발 노드에서 네트워크의 모든 다른 노드로 가는 경로가 존재하고, 네트워크에 음수 가중치 사이클이 없으면 유일하고 유한한 해를 가진다.
Bellman-Ford method
벨만포드 메서드는 벨만 방정식을 푸는 메서드 중 하나이다.
Stage1.

(1)은 link를 하나만 거친다는 뜻이다.
Stage2 로 간다.
Stage2.
$u_j^{(1)}$을 $u_j^{(2)}$로 업데이트해준다.

만약 $u_j^{(2)}=u_j^{(1)}$ 라면, 최단 경로인 것이므로 업데이트를 중지한다.
이전 스테이지 m-1에 대한 업데이트가 m 스테이지에서 이루어지고,


이면 업데이트를 중단한다.
$u_j^{(m)}$은 노드 1에서 노드 j까지의 최단 경로 길이이며, 경로는 최대 m개의 링크를 포함할 수 있다는 뜻이다.
각 노드 j에 대해, $u_j^{(m)}$는 비증가 순서를 가진다. 즉, m이 증가함에 따라 $u_j^{(m)}$는 변하지 않거나 줄어든다. 이는 반복할수록 최단 경로 길이가 점점 개선됨을 의미한다.
벨만 포드 방법은 반드시 E(간선의 개수)단계 이내에 종료해야한다. 계산 복잡도는 $O(n^3)$이다.
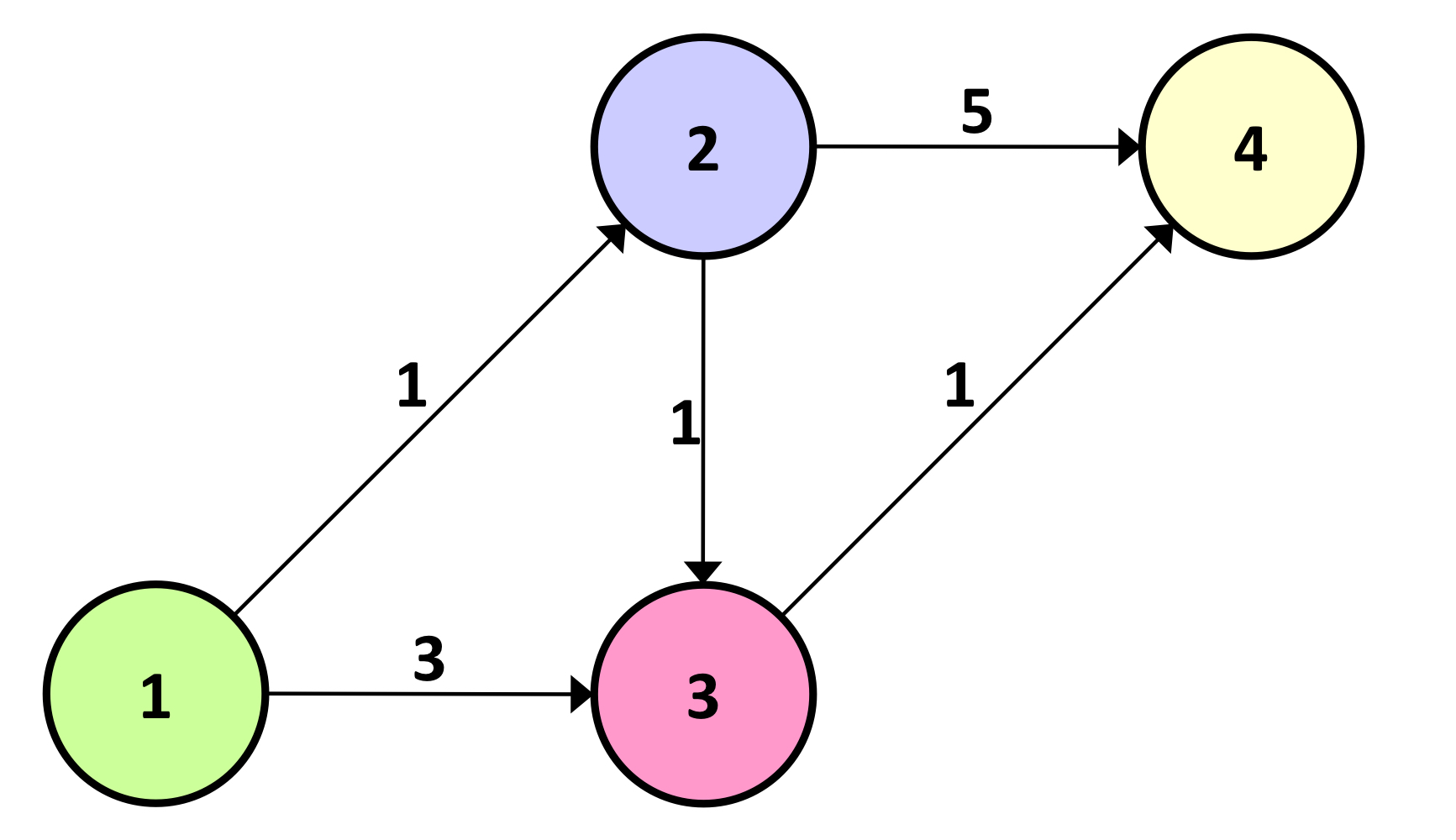
위 사진처럼 생긴 네트워크가 있다. 노드 1에서 부터 모든 노드(2, 3, 4)까지의 최단 경로를 구하면 된다.
Stage1.
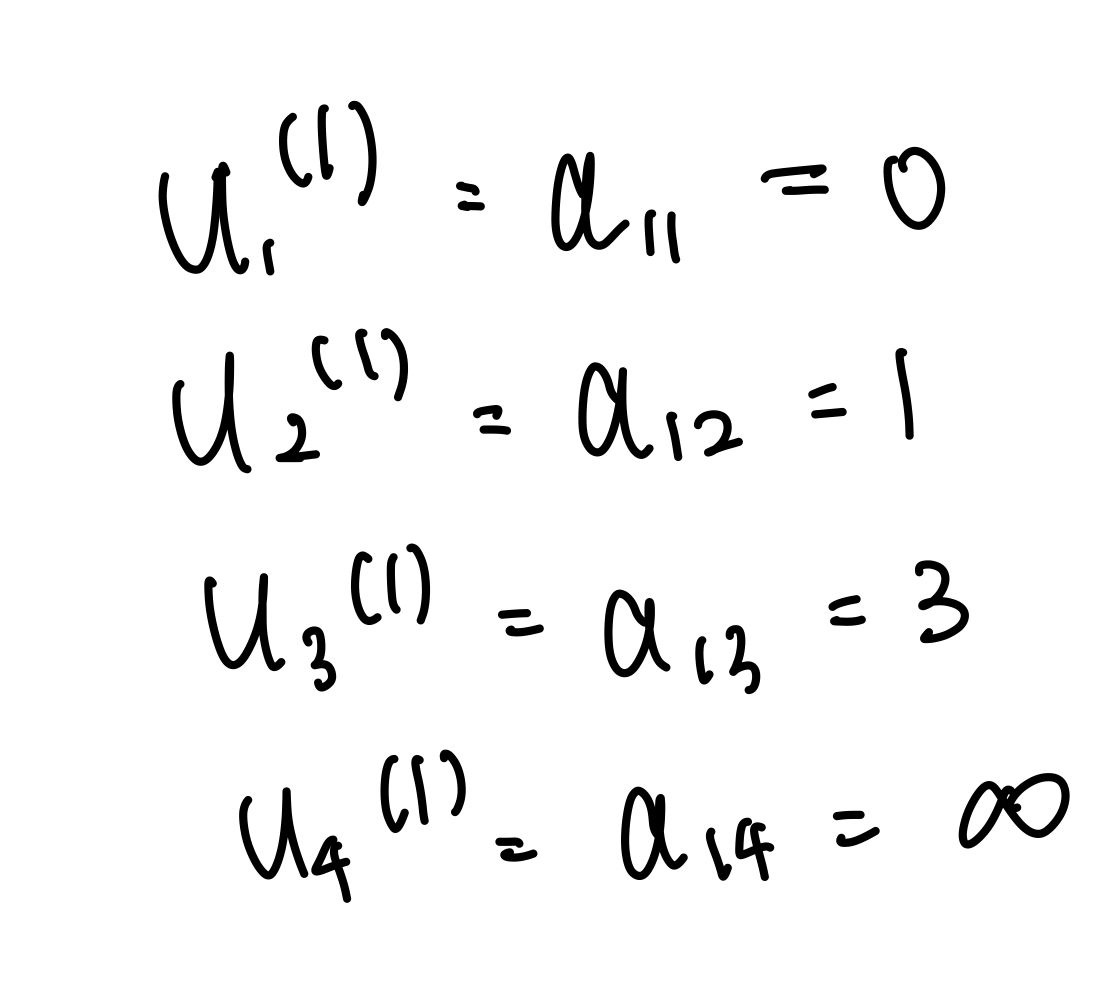
Stage2.
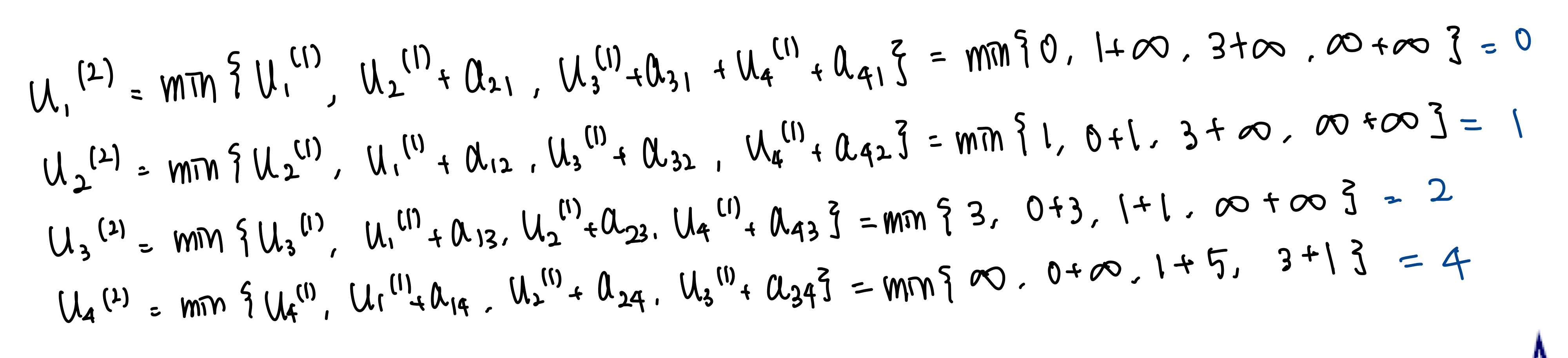
$u_3^{(2)} < u_3{(1)}$ 이고, $u_4^{(2)} < u_4{(1)}$ 이므로, Stage3 으로 가야한다.

$u_4^{(3)} < u_4{(2)}$ 이므로, Stage4 로 가야한다.
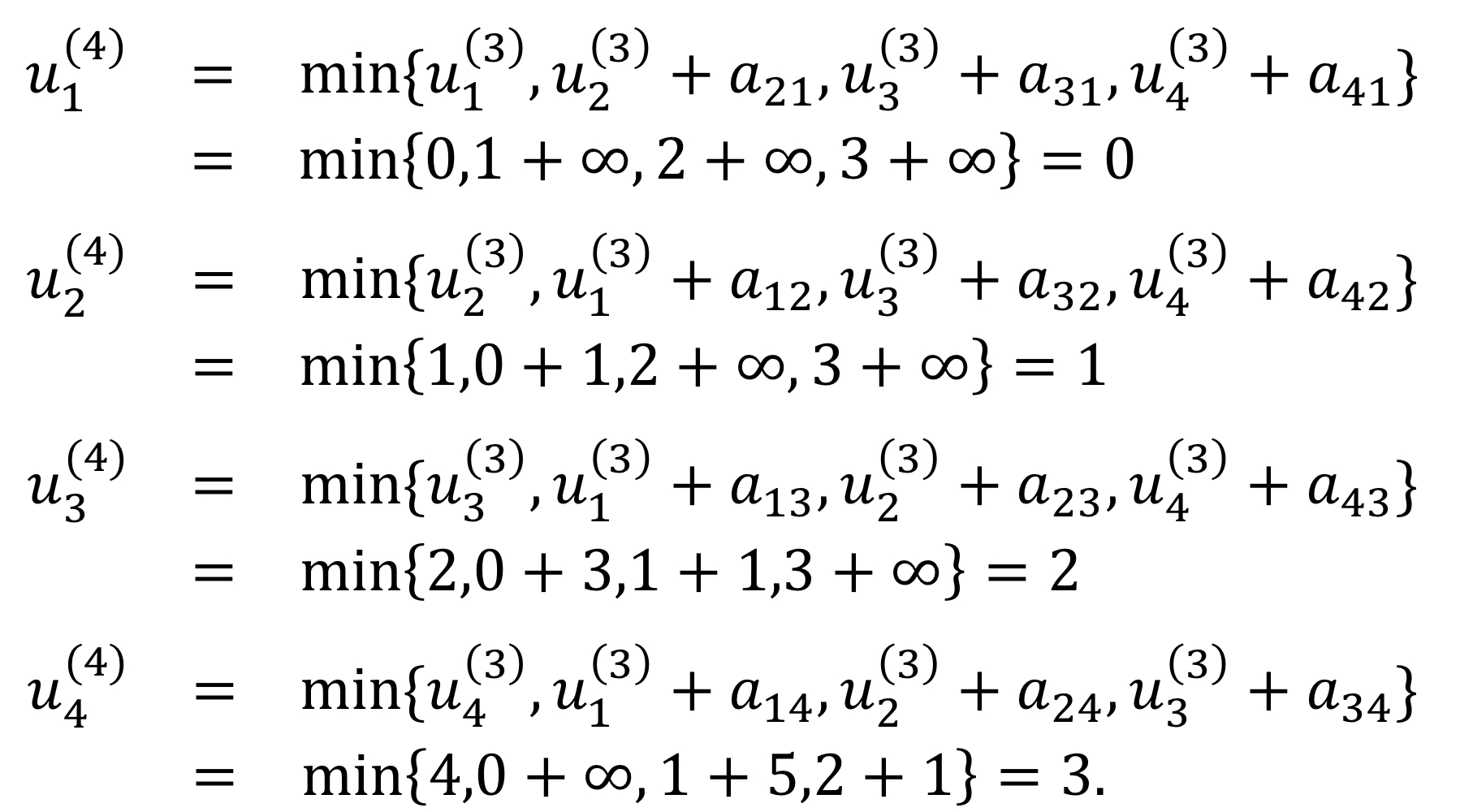
이렇게 모든 업데이트가 끝이났다.
그러므로 $u_1, u_2, u_3, u_4$ 는 각각 0, 1, 2, 3이 된다.

Dijkstra method
다익스트라 메서드는 벨만 방정식을 푸는 또다른 메서드다.
P는 영구 라벨을 가진 노드 집합이다. 이 집합에 포함된 노드는 최단 경로의 길이가 확장된 노드들로 구성된다. 즉, 출발점에서 이 노드까지의 진정한 최단 경로 길이가 이미 발견된 상태인 것이다.
T는 임시 라벨을 가진 노드 집합이다. 이 집합에 포함된 노드는 조건부로 최단 경로 길이가 계산된 상태이다. 즉, 출발점에서 이 노드까지의 경로 길이가 확정되지 않았으며, 더 짧은 경로가 발견될 가능성이 있다.
Step0.

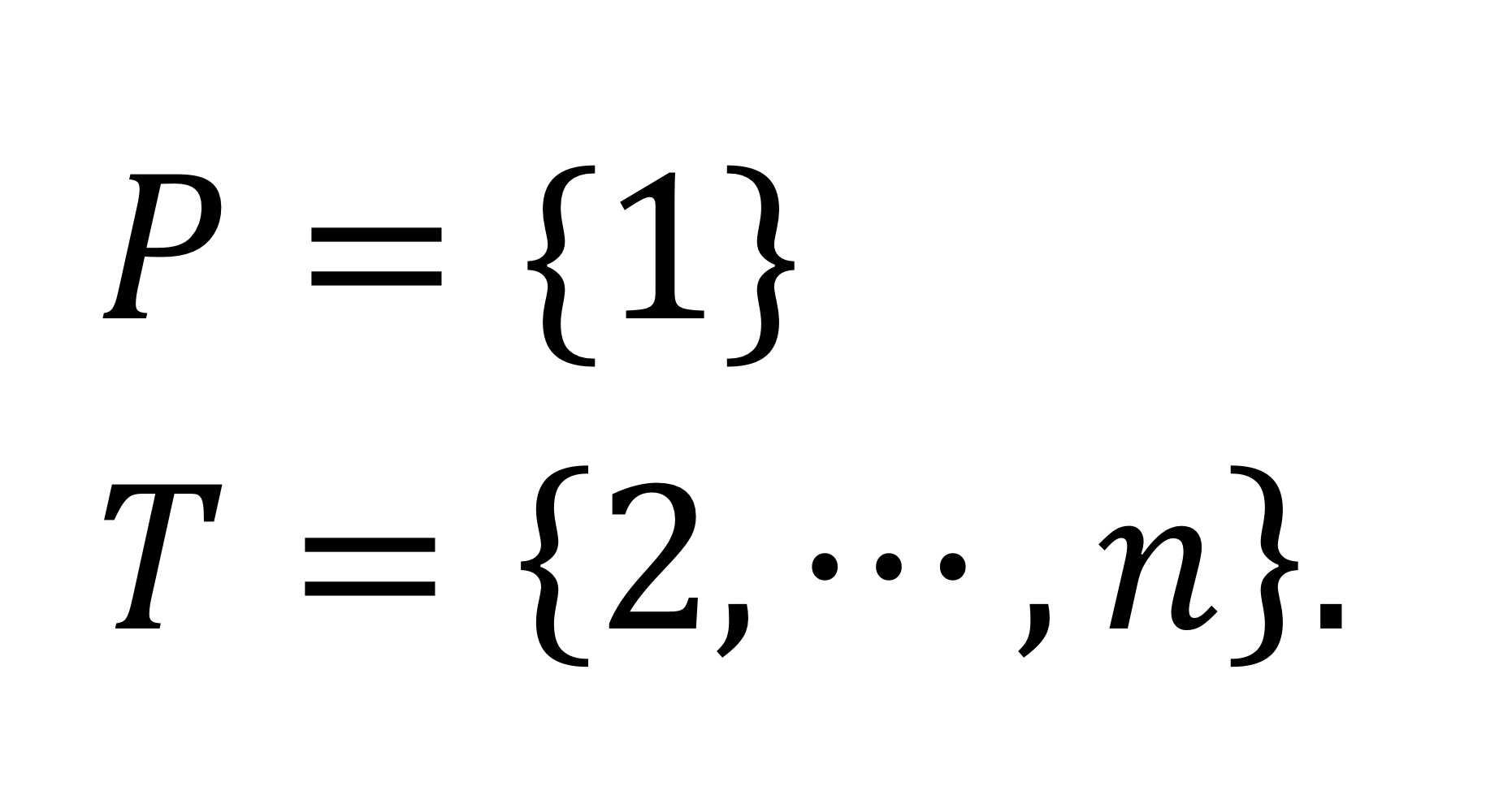
시작 노드는 이미 최단 경로 길이이므로, 집합 P에 들어가있다.
Step1.
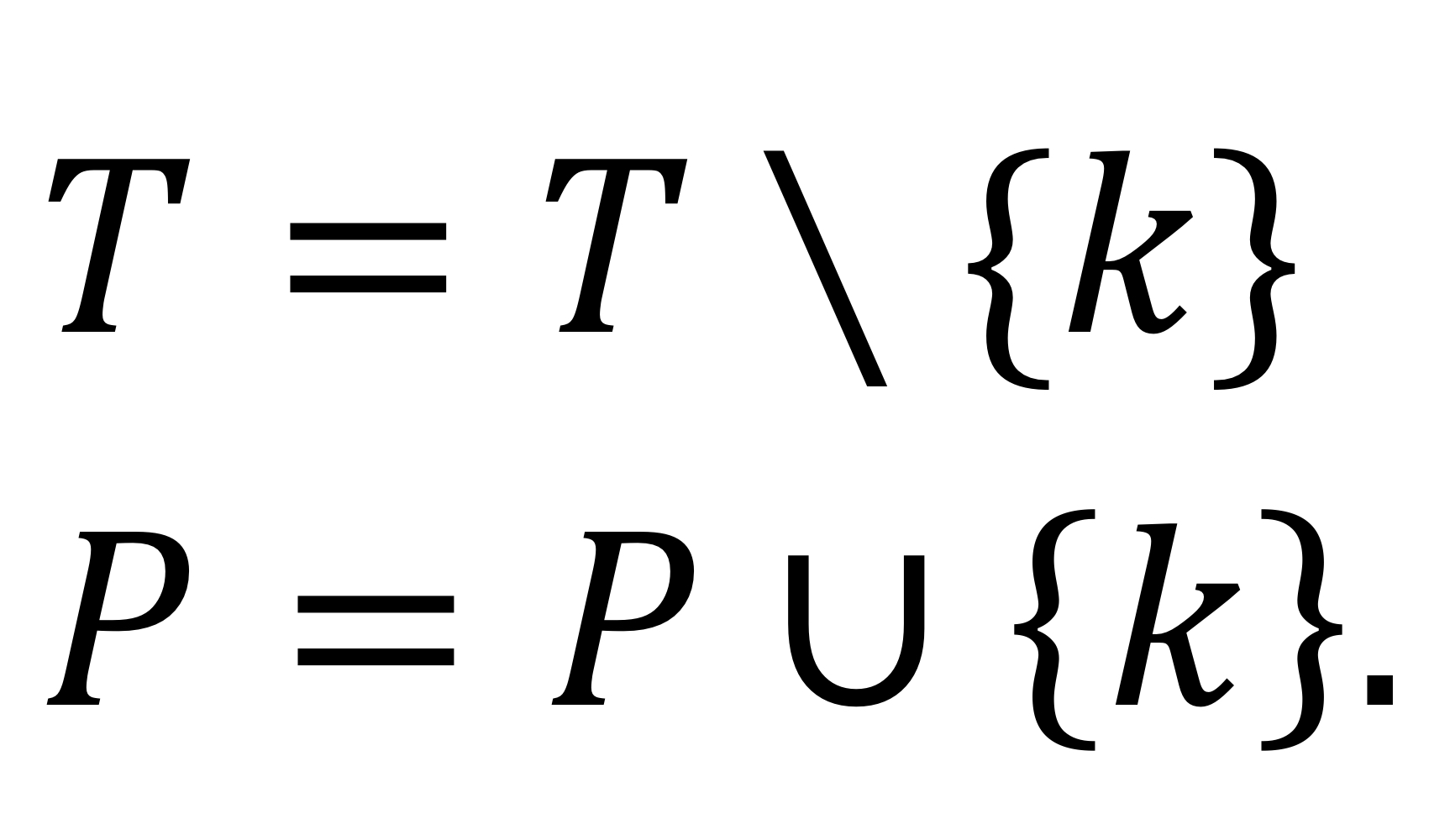
T 집합에 있는 노드 k 중에서, $u_k$ = min{$u_j : j \in T$} 이면 노드 k를 집합 P로 이동한다.
만약 T가 빈 집합이 된다면 중단하고, 아니면 Step2를 진행한다.\
Step2.

집합 T의 모든 노드 j에 대해 진행한다.
다시 Step 1을 진행한다. 집합 T가 빈 집합이 될 때까지 반복한다.
다익스트라 메서드는 출발노드에서 다른 모든 노드로 가는 경로가 존재해야 하며, 모든 링크가 양수여야 유일하고 유한한 해를 구할 수 있다.
음수 가중치 간선이 있는 경우, 다익스트라 알고리즘은 올바른 해를 보장하지 못한다.
다익스트라 메서드의 계산 복잡도는 $O(n^2)$으로, 벨만 포드 메서드보다 짧다.
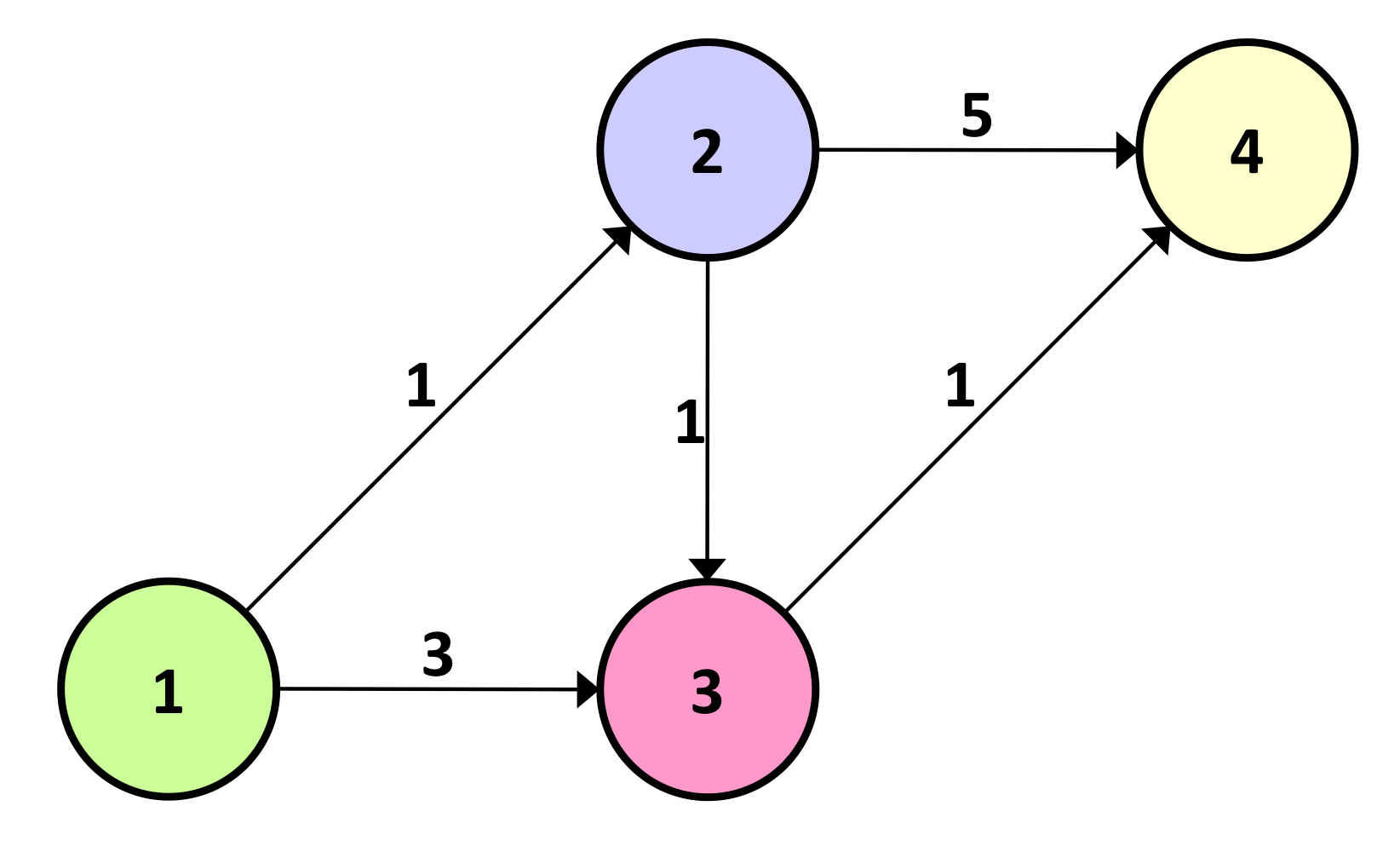
Step 0.

Step 1.
T = {2, 3, 4}에서 가장 작은 값을 가지는 것은 $u_2$=1 이므로, P로 이동한다.
P ={1, 2}, T= {3, 4}
Step 2. & Step 1.

가장 작은 값을 가지는 것은 $u_3$ = 2이므로, P로 이동한다.
P = {1, 2, 3}, T = {4}
Step 2. & Step 1.
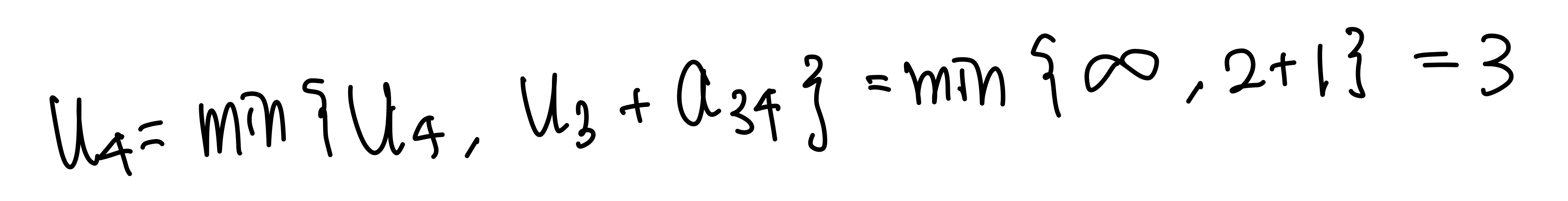
$u_4$를 P로 이동시켜주면 T는 공집합이 되고, 업데이트는 끝이 난다.

Source routing schem
소스 노드는 목적지 노드에 도달하는 고유한 경로를 결정한다. 경로를 따라 있는 모든 노드에 라우팅 테이블이 생성되며, 목적지 노드로 향하는 모든 패킷은 해당 경로를 따라 전달된다.
각 노드는 라우팅 테이블을 읽고 경로를 따라 다음 노드로 패킷을 전달한다.
소스 라우팅 방식의 특징
- 경로 상의 노드는 경로를 찾기 위해 추가적인 계산을 할 필요가 없다.
- 최단 경로 라우팅 방식보다 단순하다.
- 소스 라우팅 방식에서 결정된 경로는 최적일 필요가 없다.
- 따라서 최단 경로 라우팅 방식보다 효율이 낮다.

위 사진과 같은 네트워크에서, 노드 1에서 노드 4로 패킷을 전달하려 한다고 가정한다.
소스 라우팅 방식을 따라 패킷을 전달한다.
노드 1에서 노드 4로 가는 세 가지 경로가 존재한다. {1, 2, 4}, {1, 3, 4}, {1, 2, 3, 4}
노드 1이 경로 {1, 2, 4}를 사용하기로 결정했다.
후에 시그널링 단계에서, 노드2에 룩업 테이블이 생성된다. 이 테이블은 노드 1에서 수신된 모든 패킷이 링크 (2, 4)를 통해 노드 4로 전송되어야 함을 나타낸다.
노드 1은 패킷을 링크(1, 2)를 통해 통해 노드2로 전송하며, 노드 1로부터 패킷을 수신한 노드 2는 테이블을 참조하여 링크 (2, 4)를 통해 해당 패킷을 노드 4로 전송한다.
- 경로 {1, 2, 4}의 길이는 6이다.
- 경로 {1, 3, 4}의 길이는 4이다.
- 경로 {1, 2, 3, 4}의 길이는 3이다.
그러나, 노드 1은 어떤 경로가 최단 경로인지 알지 못할수도 있다. 따라서, 노드1이 경로 {1, 2, 3, 4}를 사용하기로 결정하지 못할수도 있다.설령 노드 1이 경로 {1, 2, 3, 4}를 사용하기로 결정하더라도, 세션 도중 경로 내 링크의 길이가 변경될 수 있다.
Random routing scheme
노드에 전달할 패킷이 있는 경우, 노드는 모든 가능한 출력 링크 중 하나를 동일한 확률로 선택한다. 선택된 출력 링크를 통해 패킷을 전송한다.
랜덤 라우팅 방식의 특징
- 노드는 네트워크에 대한 정보를 전혀 필요로 하지 않는다.
- 최단 경로 라우팅 방식보다 적은 정보를 필요로 한다.
- 랜덤 라우팅 방식에서 결정된 경로는 최적이 아닐 수 있다.
- 따라서 최단 경로 라우팅 방식보다 비효율적이다.
- 경로가 존재하더라도, 랜덤 라우팅 방식은 목적지 노드로의 경로를 찾지 못할 수도 있다.

위 사진과 같은 네트워크에서, 노드 1에서 노드 4로 패킷을 전달하려 한다고 가정한다.
랜덤 라우팅 방식에 따라 패킷을 전달한다.
노드 1은 두 링크 (1, 2)와 (1, 3) 중 하나를 동일한 확률로 선택한다. 링크 (1, 2)를 선택했다고 가정한다.
그런 다음, 노드 1은 (1, 2)를 통해 노드 2로 패킷을 전송한다.
패킷을 수신한 노드 2는 링크(2, 3)과 (2, 4) 중 하나를 동일한 확률로 선택한다. 링크 (2, 4)를 선택했다고 가정한다.
그런 다음, 노드 2는 링크 (2, 4)를 통해 노드 4로 패킷을 전송한다.
노드 1에서 노드 4로 가는 세 가지 경로가 존재한다. {1, 2, 4}, {1, 3, 4}, {1, 2, 3, 4}
- 경로 {1, 2, 4}를 선택하는 확률은 1/2 × 1/2 = 1/4 이다.
- 경로 {1, 3, 4}를 선택하는 확률은 1/2 × 1 = 1/2 이다.
- 경로 {1, 2, 3, 4}를 선택하는 확률은 1/2 × 1/2 × 1 = 1/4 이다.
따라서, 노드 1에서 노드 4로 패킷을 전달하기 위한 경로의 평균 길이는 6 × 1/4 + 4 × 1/2 + 3 × 1/4 = 17/4 = 4.25 이다.
Flooding scheme
노드에 전달할 패킷이 있는 경우, 노드는 출력 링크 수만큼 패킷의 복사본을 생성한다. 노드는 각 출력 링크를 통해 패킷 복사본을 전송한다.
플러딩 방식의 특징
- 노드는 네트워크에 대한 정보를 필요로 하지 않는다.
- 최단 경로 라우팅 방식보다 적은 정보를 필요로 하며, 최단 경로 라우팅 방식보다 더 많은 자원을 사용한다.
- 플러딩 방식을 사용하는 동안 자원을 절약하기 위해, 패킷 헤더에 해당 패킷이 통과한 노드 이름을 기록할 수 있으며, 패킷의 수명을 제한할 수 있다.
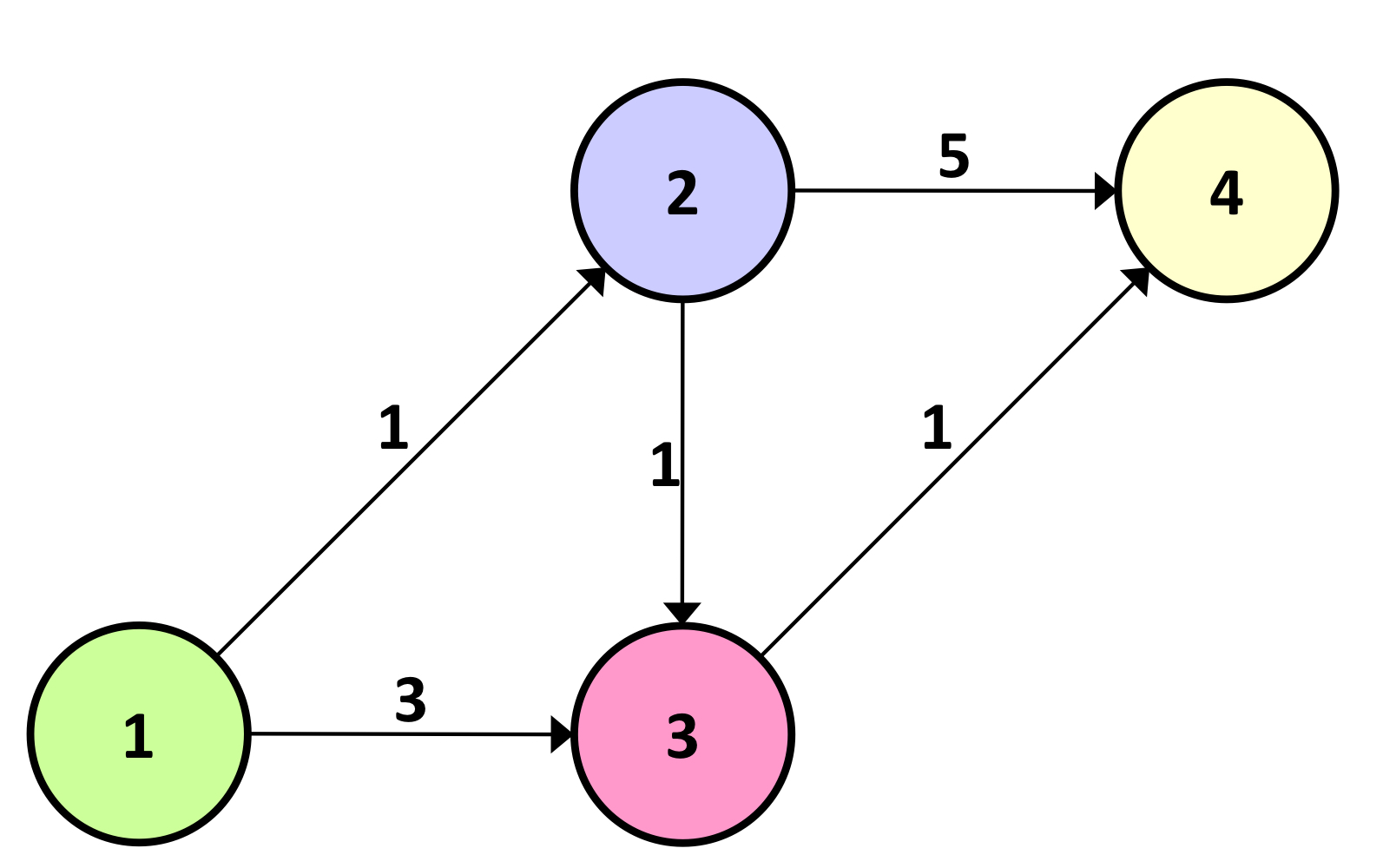
위 사진과 같은 네트워크에서, 노드 1에서 노드 4로 패킷을 전달하려 한다고 가정한다.
플러딩 방식을 따라 패킷을 전달한다.
노드 1에는 두 개의 출력 링크가 있으므로, 노드 1은 패킷의 복사본 두 개를 생성한다.
그런 다음, 노드 1은 링크(1, 2)와 (1, 3)를 통해 각각 노드 2와 노드 3으로 패킷 복사본을 전송한다.
노드 1로부터 패킷 복사본을 수신한 노드 2는 출력 링크가 두 개 있으므로, 패킷의 복사본 두 개를 생성한다.
그런 다음, 노드 2는 링크 (2, 3)과 (2, 4)를 통해 각각 노드 3과 노드 4로 패킷 복사본을 전송한다.
노드 1로부터 패킷 복사본을 수신한 노드 3은 출력 링크가 하나 뿐이므로, 패킷 복사본 한 개를 생성한다.
그런 다음, 노드 3은 링크 (3, 4)를 통해 노드 4로 패킷 복사본을 전송한다.
노드 2로부터 패킷 복사본을 수신한 노드 3은 출력 링크 링크가 하나 뿐이므로, 패킷 복사본 한 개를 생성한다.
그런 다음, 노드 3은 링크(3, 4)를 통해 노드 4로 패킷 복사본을 전송한다.
- 노드 1은 패킷을 두 번 전송한다.
- 노드 2는 패킷을 한 번 수신하고, 두 번 전송한다.
- 노드 3은 패킷을 두 번 수신하고, 두 번 전송한다.
- 노드 4는 패킷을 세 번 수신한다.
** 대학교 수업을 듣고 이해한 부분을 최대한 풀어서 작성한 글입니다.
틀린 정보가 존재할 수 있으며, 언제나 피드백은 환영입니다. **
'DKU > 데이터 통신' 카테고리의 다른 글
| HDLC(High-level Data Link Protocol) (0) | 2024.12.03 |
|---|---|
| Flow Control (0) | 2024.11.26 |
| Error Control 6 (0) | 2024.11.20 |
| Error Control 5 (0) | 2024.11.19 |
| ARQ for Deep Space Communications 과제 분석 (2) | 2024.11.16 |
